Понятие корреляционной связи

Лекция 6. Элементы корреляционного и регрессионного анализа

В математике для описания связей между переменными величинами используют понятие функции F, которая ставит в соответствие каждому определенному значению независимой переменной X определенное значение зависимой переменной Y. Такого рода однозначные зависимости между пере­менными величинами X и У называют функциональными. Но подобные однозначные, или функциональные, связи между переменными величинами встречаются далеко не всегда

Поэтому, связи между психологическими признаками имеют не функциональный, а статистический характер, когда в среднем определенному значению одного признака, например, выраженной акцентуации подростков по гипертимному типу, рассматриваемому в качестве аргумента, соответствует не одно какое-либо значение, а целый спектр, распределяющихся в вариационный ряд числовых значений, например, такого психологического признака, как тревожность, который можно рассматривать в качестве зависимой переменной или функции. Такого рода зависимость между переменными величинами называется корреляционной, или корреляцией. Корреляционная связь — это согласованное изменение двух признаков, отражающее тот факт, что изменчивость одного признака находится в соответствии с изменчивостью другого.

Функциональные связи легко обнаружить и измерить на единичных и групповых объектах, однако этого нельзя проделать с корреляционными связями, которые можно изучать только на представительных выборках методами математической статистики. Корреляционные связи — это вероятностные изменения.

Виды корреляционных связей между измеренными признака­ми могут быть различны: так, корреляция бывает линейной и нелинейной, положительной и отрицательной. Она линейна — если с увеличением или уменьшением одной переменной X, вторая переменная Y всреднем либо также растет, либо убывает. Она нелинейна, если при увеличении одной величины характер изменения второй не лине­ен, а описывается другими законами.

Корреляция будет положительной, если с увеличением переменной X переменная Y в среднем также увеличивается, а если с увеличением X переменная Y имеет в среднем тенденцию к уменьшению, то говорят о наличии отрицательной корреляции.

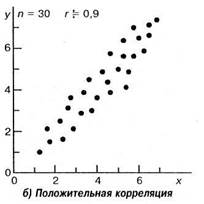
Возможна ситуация, когда между переменными невозможно установить какую-либо зависимость. В этом случае говорят об отсутствии корреляционной связи. Подчеркнем, однако, что нередко встречаются задачи, в которых традиционная и наиболее часто встречающаяся в психологических исследованиях ли­нейная корреляционная связь отсутствует, в то время как имеется высокозначимая криволинейная связь, например, полиномиальная или гиперболическая.

Степень, сила или теснота корреляционной связи определяется по величине коэффициента корреляции.

Сила связи не зависит от ее направленности и определяется по абсолютному значениюкоэффициента корреляции. Максимальное возможное значение коэффициента корреляции ; минимальное .

Используются две системы классификации корреляционных связей по их силе: общая и частная. Общая классификация корреляционных связей:

1) сильная, или тесная при коэффициенте корреляции ;

2) средняя при ;

3) умеренная при ;

4) слабая при ;

5) очень слабая при

Частная классификация корреляционных связей:

1) высокая значимая корреляция при , соответствующем уровню статистической значимости ;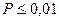

2) значимая корреляция при , соответствующем уровню статистической значимости ;

3) тенденция достоверной связи при , соответствующем уровню статистической значимости ;

4) незначимая корреляция при , не достигающем уровня статистической значимости.

Две эти классификации не совпадают. Первая ориентирована только на величину коэффициента корреляции, а вторая определяет, какого уровня значимости достигает данная величина коэффициента корреляции при данном объеме выборки. Чем больше объем выборки, тем меньше величины коэффициента корреляции оказывается достаточно, чтобы корреляция была признана достоверной. В результате при малом объеме выборки может оказаться так, что сильная корреляция окажется недостоверной. В то же время при больших объемах выборки даже слабая корреляция может оказаться достоверной.

Обычно принято ориентироваться на вторую классификацию, так как она учитывает объем выборки. Вместе с тем, необходимо помнить, что сильная, или высокая, корреляция – это корреляция с коэффициентом , а не просто корреляция высокого уровня значимости.

Задача корреляционного анализа сводится кустановлению направления (положительное или отрицательное) и формы (ли­нейная, нелинейная) связи между варьирующими признаками, измерению ее тесноты, и, наконец, к проверке уровня значимо­сти полученных коэффициентов корреляции.

Зависимость между коррелирующими переменными X и У, как и в математике, можно выразить с помощью формул и урав­нений (т.е. аналитически), аможно выразить графически.

Графики корреляционных зависимостей строят по уравнени­ям следующих функций:

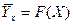или

которые называются уравнениями регрессии. Здесь и ,так на­зываемые, условные средние арифметические переменных Х и Y.

Переменные X и У могут быть измерены в разных шкалах, именно это определяет выбор соответствующего коэффициента корреляции. Представим соотношения между типами шкал, в ко­торых могут быть измерены переменные Х и У и соответствую­щими мерами связи в виде таблицы 1:

Таблица 1.

 

Тип шкалы	Мера связи
Переменная	Переменная
Интервальная или отношений	Интервальная или отношений	Коэффициент Пирсона
Ранговая, интервальная или отношений	Ранговая, интервальная или отношений	Коэффициент Спирмена
Ранговая	Ранговая	Коэффициент «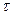» Кендалла
Дихотомическая	Дихотомическая	Коэффициент «»
Дихотомическая	Ранговая	Рангово-бисериальный
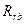
Дихотомическая	Интервальная или отношений	Бисериальный
Интервальная	Ранговая	Не разработан

 

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: