 |
Доверительный интервал для дисперсии.
|
|
|
|
Вариант 11
Задание 1
Рабочий обслуживает четыре станка. Вероятность того, что в течение часа первый станок не потребует внимания рабочего, равна 0,3, второй - 0,4; третий – 0,7. Найти вероятность того, что в течение часа:
а) ни один станок не потребует внимания рабочего;
б) хотя бы один станок потребует внимания рабочего;
в) только один станок потребует внимания рабочего;
Решение:
а) В – событие, где все 3 станка не потребуют внимания рабочего в течение часа. Тогда искомая вероятность равна:
Р(В)=Р(А1*А2*А3)=Р(А1)*Р(А2)*Р(А3)=0,3*0,4*0,7=0,084
б) Найдём вероятность через противоположное событие, т.е. ни один станок не потребует внимания рабочего в течение часа
Р(С)=1–0,084 = 0,916.
в) Ᾱ (i =1,2,3) – потребует i-й внимания станок, независимое событие
Р (Ᾱ1) = 1 – 0,3 = 0,7
Р (Ᾱ2) = 1 – 0,4 = 0,6
Р (Ᾱ3) = 1 – 0,7 = 0,3
Р(В)=Р(А1*Ᾱ2*А3+Ᾱ1*А2*А3+А1*А2*Ᾱ3)=(0,3*0,6*0,7+0,7*0,4*0,7+0,3*0,4*0,3)=0,358
Ответ: а) вероятность равна 0,084, что в течение часа ни один станок не потребует внимания рабочего; б) вероятность равна 0,916, что в течение часа хотя бы один станок потребует внимания рабочего; в) вероятность равна 0,358, что в течение часа только один станок потребует внимания рабочего.
Задание 2.
Вероятность прибытия поезда без опоздания равна 0,9. Считая опоздания различных поездов независимыми событиями, найти вероятность того, что из 5 поездов опоздает не более одного.
Решение:
Вероятность обратного события «поезд не опоздал» равна q=1-0.9=0.1. Тогда искомая вероятность, что из 5 поездов опоздает не более одного равна:
 .
.
Ответ: вероятность того, что из 5 поездов опоздает не более одного равна 0,00046, т.е. событие маловероятно.
Задание 3.
Даны законы распределения двух независимых случайных величин:
|
|
|
| Значение Х | ||||
| Вероятность | 0,4 | 0,2 | 0,1 | 0,3 |
| Значение У | |||
| Вероятность | 0,5 | 0,25 | 0,25 |
Составить закон распределения их разности, а затем проверить выполнение формул М(Х-Y)=М(Х)-М(Y); D(X-Y)=D(X)+D(Y).
Решение:
Составим закон распределения разности двух независимых случайных величин. Разностью двух событий A и B называется третье событие A\B, которое происходит тогда, когда происходит событие A и одновременно с этим не происходит событие В.
| Значение Z=Х-У | 2-0 | 4-1=3 | 6-2=4 | 8-0=8 |
| Вероятность | 0,2 | 0,15 | 0,075 | 0,34 |



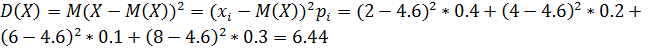


Проверим выполнение формул:
М(Х-Y)=М(Х)-М(Y)=4,6-0,75=3,85;
D(X-Y)=D(X)+D(Y)=6,44+0,69=7,13
Все формулы выполняются.
Задание 4
По заданной функции распределения F(x) найти функцию плотности f(x), построить графики F(x) и f(x), найти M(X), D(X), s(x), p(a<x<b)

Решение:

Построим графики данных функций:




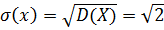

Задание 5.
На опытном участке имеется 10000 колосьев хлебного злака. Требуется определить необходимый объем бесповторной выборки для того, чтобы по ее результатам определить среднюю массу колосьев на всем участке так, чтобы с веротяностью 0,991 ошибка в определении средней массы колосьев на всем участке не превысила 0,1 г. По данным пробной выборки установлено, что выборочная дисперсия равна 0,8.
Решение:
По данным можно выбрать следующие сведенья:
р=0,991,  , N=10000
, N=10000
Используя следующую формулу
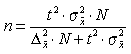

Ответ: 415 колосьев.
Задание 6.
Для данного вариационного ряда найти доверительные интервалы для среднего значения и дисперсии, проверить гипотезу нормального распределения по критерию c2 с доверительной вероятностью 0,95.
Построить гистограмму эмпирического распределения и теоретическую кривую.
Распределение квартир жилого дома по суточному потреблению электроэнергии (по дням недели):
| Потребление электроэнергии, кВт.ч | Понедельник |
| 0,75-1,25 | |
| 1,25-1,75 | |
| 1,75-2,25 | |
| 2,25-2,75 | |
| 2,75-3,25 | |
| 3,25-3,75 | |
| 3,75-4,25 | |
| 4,25-4,75 | |
| 4,75-5,25 | |
| 5,25-5,75 | |
| 5,75-6,25 | - |
| 6,25-6,75 | - |
| Итого: |
|
|
|
Решение:
Составим таблицу для расчета показателей.
| Группы | xi | Кол-во, fi | xi * fi | Накопленная частота, S | (x-xср)*f | (x-xср)2*f |
| 0.75 - 1.25 | ||||||
| 1.25 - 1 | 1.13 | 7.88 | 6.11 | 5.34 | ||
| 1.75 - 1 | 1.38 | 26.13 | 11.84 | 7.38 | ||
| 2.25 - 1 | 1.63 | 50.38 | 11.57 | 4.32 | ||
| 2.75 - 1 | 1.88 | 65.63 | 4.32 | 0.53 | ||
| 3.25 - 1 | 2.13 | 48.88 | 2.91 | 0.37 | ||
| 3.75 - 1 | 2.38 | 42.75 | 6.78 | 2.55 | ||
| 4.25 - 1 | 2.63 | 5.01 | 3.14 | |||
| 4.75 - 1 | 2.88 | 8.63 | 2.63 | 2.31 | ||
| 5.25 - 5.75 | 5.5 | 27.5 | 17.51 | 61.31 | ||
| 5.75 - 6.25 | ||||||
| 6.25 - 6.75 | 6.5 | |||||
| 299.75 | 69.69 | 88.25 |
Среднее потребление энергии
Дисперсия
Доверительный интервал для генерального среднего.
Поскольку n>30, то определяем значение tkp по таблицам функции Лапласа.
В этом случае 2Ф(tkp) = 1 - γ
Ф(tkp) = (1 - γ)/2 = 0.95/2 = 0.475
По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 0.475
tkp(γ) = (0.475) = 1.96
(2 - 0.12;2 + 0.12) = (1.88;2.12)
С вероятностью 0.95 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала.
Доверительный интервал для дисперсии.
Вероятность выхода за нижнюю границу равна P(χ2n-1 < hH) = (1-γ)/2 = 0.025. Для количества степеней свободы k = 149, по таблице распределения хи-квадрат находим:
χ2(149;0.025) = 185.8004.
Случайная ошибка дисперсии:
Вероятность выхода за верхнюю границу равна P(χ2n-1 ≥ hB) = 1 - P(χ2n-1 < hH) = 1 - 0.025 = 0.975. Для количества степеней свободы k = 149, по таблице распределения хи-квадрат находим:
χ2(149;0.975) = 117.9845.
Случайная ошибка дисперсии:
(0.59 - 0.47; 0.59 + 0.75)
(0.12; 1.34)
Найдем верхнюю границу доверительного интервала для среднеквадратического отклонения с надежностью γ = 0.95.
P(χ2n-1 > hγ) = 0.95. Для количества степеней свободы k = 149, по таблице распределения хи-квадрат находим:
χ2(149;0.95) = 122.6918.
Случайная ошибка дисперсии:
Проверим гипотезу о том, что Х распределено по нормальному закону с помощью критерия согласия Пирсона.
где pi — вероятность попадания в i-й интервал случайной величины, распределенной по гипотетическому закону
|
|
|
Для вычисления вероятностей pi применим формулу и таблицу функции Лапласа
| Интервалы группировки | Наблюдаемая частота ni | Ф(xi) | Ф(xi+1) | Вероятность pi попадания в i-й интервал | Ожидаемая частота npi | Слагаемые статистики Пирсона Ki |
| 0.75 - 1.25 | 0.34 | 0.45 | 0.11 | 16.79 | 14.84 | |
| 1.25 - 1 | 0.4 | 0.34 | 0.0667 | 10.01 | 0.9 | |
| 1.75 - 1 | 0.4 | 0.13 | 0.27 | 41.09 | 11.87 | |
| 2.25 - 1 | 0.4 | 0.13 | 0.27 | 41.09 | 2.48 | |
| 2.75 - 1 | 0.4 | 0.34 | 0.0667 | 10.01 | 62.44 | |
| 3.25 - 1 | 0.4 | 0.45 | 0.0452 | 6.78 | 38.8 | |
| 3.75 - 1 | 0.4 | 0.49 | 0.0855 | 12.83 | 2.09 | |
| 4.25 - 1 | 0.4 | 0.5 | 0.0952 | 14.28 | 2.76 | |
| 4.75 - 1 | 0.4 | 0.5 | 0.0966 | 14.5 | 9.12 | |
| 5.25 - 5.75 | 0.5 | 0.5 | ||||
| 5.75 - 6.25 | 0.5 | 0.5 | ||||
| 6.25 - 6.75 | 0.5 | 0.5 | ||||
| 145.31 |
Определим границу критической области. Так как статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то чем больше ее наблюдаемое значение Kнабл, тем сильнее довод против основной гипотезы.
Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞).
Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения «хи-квадрат» и заданным значениям s, k (число интервалов), r=2 (параметры xcp и s оценены по выборке).
Kkp = 19.02277; Kнабл = 145.31
Наблюдаемое значение статистики Пирсона попадает в критическую область: Кнабл > Kkp, поэтому есть основания отвергать основную гипотезу. Данные выборки распределены не по нормальному закону.
Построим гистограмму:

Теоретическая кривая:

|
|
|


