 |
Множества и их свойства. Функции.
|
|
|
|
ГЛАВА 1. МНОЖЕСТВА. ЧИСЛОВЫЕ МНОЖЕСТВА.
В математике все понятия делятся на первичные и определяемые через первичные или уже известные. Основным первичным понятием математики, ее фундаментом является понятие множество. Слова «совокупность», «семейство», «система», «набор», «объединение» являются синонимами слова «множество». Под множеством понимается некоторая совокупность объектов, которые объединены в одну группу по некоторым признакам. Примеры множеств: множество учащихся в аудитории; совокупность тех из них, кто получает по математике только отличные оценки; семейство звезд Большой Медведицы; множество страниц книги; множество всех целых положительных чисел и т. д. Из приведенных примеров следует, что множество может содержать конечное или бесконечное число объектов произвольной природы. Первичными понятиями являются также точка, прямая и плоскость. Для всех остальных понятий будут даны определения.
Объекты, образующие множества называются элементами или точками множества. Множества будем обозначать: А, В,…, X, Y…, а соответствующие элементы: а,b …,x, y… Если а есть элемент множества А, то пишут  . Если a не является элементом множества А, то пишут
. Если a не является элементом множества А, то пишут  .
.
Два множества А и В называются равными, если они состоят из одних и тех же элементов и пишут  .
.
Элементы множества записываются в скобках, например: 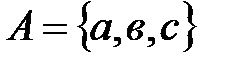 .Если множество А состоит из элементов
.Если множество А состоит из элементов  , то записывают
, то записывают  , или
, или  . Например,
. Например,  - множество целых положительных чисел, которые называются натуральными числами.
- множество целых положительных чисел, которые называются натуральными числами.
Имеет место понятие пустого множества, т.е. множества, не содержащего ни одного элемента, и его обозначают Ø.
Определение 1.  Множество А называется подмножеством множества В, если все элементы множества А являются элементами множества В. Обозначается:
Множество А называется подмножеством множества В, если все элементы множества А являются элементами множества В. Обозначается:  .
.
|
|
|

 .
.
Пустое множество содержится в любом множестве, т.е. Ø  А. Из определения также следует, что
А. Из определения также следует, что  .
.
Рассмотрим операции над множествами. Пусть А и В два множества.
Определение 2. Объединением (суммой) множеств А и В называется такое множество S, каждый элемент которого принадлежит хотя бы одному множеству А или В. Обозначение: 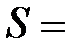
 .
.
Объединение конечного числа множеств  есть:
есть:  , т.е. x принадлежит хотя бы одному из множеств. Можно говорить об объединении бесконечного числа множеств.
, т.е. x принадлежит хотя бы одному из множеств. Можно говорить об объединении бесконечного числа множеств.
.
Определение 3. Пересечением (произведением) двух множеств А и В называется такое множество P, которое состоит из элементов множества А и элементов множества В.
 .
.
Пересечение конечного числа множеств  есть
есть  .
.
Определение 4. Разностью двух множеств А и В называется множество D, которое состоит из элементов множества А, но не принадлежащих множеству В.
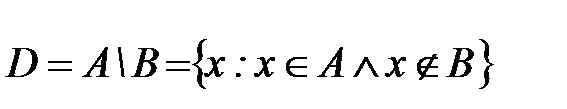
Если  , то множество
, то множество  называется дополнением множества В до множества А.
называется дополнением множества В до множества А.
Определение 5. Симметрической разностью двух множеств А и В называется множество С =  . Обозначается: С=А ∆ В.
. Обозначается: С=А ∆ В.
Свойства операций над множествами:
1. 
2.Если 
3. Если 
4.  Ø
Ø 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
Доказательство этих свойств весьма просто. Например, для доказательства равенства двух множеств надо доказать, что элемент принадлежащий левой части равенства принадлежит и правой.
Пусть заданы два множества  и
и  . Два элемента, записанные в виде
. Два элемента, записанные в виде  , где
, где 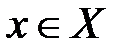 и
и  будем называть упорядоченной парой элементов или просто парой.
будем называть упорядоченной парой элементов или просто парой.
Определение 6. Декартовым произведением множеств Х и Y называется множество всех упорядоченных пар  , где
, где  ,
,  и обозначается
и обозначается  , т.е.
, т.е.
 .
.
Определение 7. Подмножество F декартового произведения  называется отображением множества Х в множество Y, если выполняется следующее условие:
называется отображением множества Х в множество Y, если выполняется следующее условие:  существует единственная пара
существует единственная пара 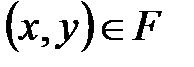 . Обозначения:
. Обозначения: 
|
|
|
Из определения следует, что не всякое подмножество  является отображением Х в Y. Например, если
является отображением Х в Y. Например, если  , а
, а  , то
, то  - отображение, но
- отображение, но 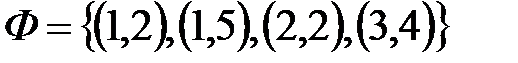 - не отображение. То есть, первые элементы в F должны быть все различные. Синонимами термина «отображение» являются следующие: функция, преобразование, соответствие, морфизм. Они отличаются буквенной символикой и сферами (разделами математики) употребления. В математическом анализе обычно используют термин «функция». Часто дают и другое определение функции, не используя термин «отображение».
- не отображение. То есть, первые элементы в F должны быть все различные. Синонимами термина «отображение» являются следующие: функция, преобразование, соответствие, морфизм. Они отличаются буквенной символикой и сферами (разделами математики) употребления. В математическом анализе обычно используют термин «функция». Часто дают и другое определение функции, не используя термин «отображение».
Определение 8. Функцией F заданной на множестве Х и принимающей значение на множестве Y называется правило, по которому элементу  ставится в соответствие строго один элемент
ставится в соответствие строго один элемент  . При этом пишут:
. При этом пишут:  . Обозначение функции: F, Ф, f, g,
. Обозначение функции: F, Ф, f, g,  и др.
и др.
Множество Х называется областью определения  , а множество
, а множество  y:
y:  называется множеством значений функции. Каждый элемент
называется множеством значений функции. Каждый элемент  называется аргументом или независимой переменной, а элемент
называется аргументом или независимой переменной, а элемент  или
или  - значением функции или зависимой переменной.
- значением функции или зависимой переменной.
Иногда говорят, что элемент у является образом элемента x при отображении F, а элемент х называют прообразом (одним из возможных) элемента у при отображении F.
Множество 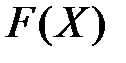 всех элементов
всех элементов 
 называется образом множества X при отображении F, т.е.
называется образом множества X при отображении F, т.е.  .
.
Пусть существует также отображение  , как множество упорядоченных пар
, как множество упорядоченных пар  . Такое отображение называется обратной функцией и это обозначают следующим образом:
. Такое отображение называется обратной функцией и это обозначают следующим образом:  .
.
Очевидны следующие тождества:

Если существуют отображения  и
и  одновременно, то отображение
одновременно, то отображение  называется взаимно-однозначным.
называется взаимно-однозначным.
Определение 9. Пусть  . Тогда отображение
. Тогда отображение 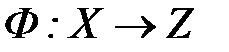 , определенное
, определенное  равенством
равенством  называется суперпозицией или сложной функцией.
называется суперпозицией или сложной функцией.
Теперь дадим определение очень важного в математическом анализе понятия.
Определение 10. Функция определения на множестве  натуральных чисел и принимающая значения из некоторого множества А называется последовательностью.
натуральных чисел и принимающая значения из некоторого множества А называется последовательностью.

Пусть  . Соответствующее значение последовательности будем обозначать
. Соответствующее значение последовательности будем обозначать 
 . Последовательность
. Последовательность  будем обозначать
будем обозначать 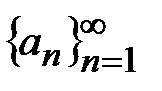 или
или  , где
, где  – члены последовательности. Таким образом, значения этой функции можно занумеровать.
– члены последовательности. Таким образом, значения этой функции можно занумеровать.
Определение 11. Множества А и В называются эквивалентными, если существует взаимно-однозначное отображение этих множеств.
|
|
|
Обозначение:  ~ B.
~ B.
Пример. Пусть  - множество натуральных чисел. Обозначим множество целых чисел
- множество натуральных чисел. Обозначим множество целых чисел  . Ясно
. Ясно  . Однако покажем, что эти множества эквивалентны. Установим следующее взаимно-однозначное соответствие между N и Z. Нечетному числу
. Однако покажем, что эти множества эквивалентны. Установим следующее взаимно-однозначное соответствие между N и Z. Нечетному числу  поставим в соответствие положительное число
поставим в соответствие положительное число  . Четному числу
. Четному числу  поставим в соответствие отрицательное
поставим в соответствие отрицательное  .
.
Полученная функция  отображает множество N на множество взаимно-однозначно, т.е. N~Z. Здесь
отображает множество N на множество взаимно-однозначно, т.е. N~Z. Здесь  и т.д.
и т.д.
Определение 12. Пусть  . Множество А называется конечным, если существует такой номер n, что А ~
. Множество А называется конечным, если существует такой номер n, что А ~  . В противном случае множество А называется бесконечным.
. В противном случае множество А называется бесконечным.
Определение 13. Бесконечное множество А называется счетным, если А~ N, в противном случае бесконечное множество называется несчетным.
Говорят, что множество А не более чем счетное, если оно либо конечно, либо счетное. Элементы такого множества можно занумеровать: 
 .
.
|
|
|


