Основные структурные алгоритмические конструкции

Элементарные шаги алгоритма можно объединить в следующие алгоритмические конструкции: линейные (последовательные), раз­ветвляющиеся, циклические с предусловием и циклические с постусловием. Любой алгоритм можно составить, используя эти четыре алгоритмические конструкции.

Линейной называют алгоритмичес­кую конструкцию, реализованную в виде последовательности действий (шагов), в которой каждое действие (шаг) алгоритма выполняется ровно один раз, причем после каждого i -го действия (шага) выполняется (i+1)-е действие (шаг), если i -е дей­ствие — не конец алгоритма.

Разветвляющейся (или ветвящейся) называется алгоритмическая конструкция, обеспечивающая выбор между двумя альтернативами в зависимости от значения входных данных. При каждом конкретном наборе входных данных разветвляющийся алгоритм сводится к ли­нейному. Различают неполное (если – то) и полное (если – то – иначе) ветвления. Полное ветвление позволяет организовать две вет­ви в алгоритме (то или иначе), каждая из которых ведет к общей точке их слияния, так что выполнение алгоритма продолжается не­зависимо от того, какой путь был выбран (рис. 1). Неполное ветв­ление предполагает наличие некоторых действий алгоритма только на одной ветви (то), вторая ветвь отсутствует, т.е. для одного из ре­зультатов проверки никаких действий выполнять не надо, управле­ние сразу переходит к точке слияния.

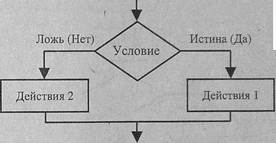
Рис. 1. Полное ветвление

Циклической (или циклом) называют алгоритмическую конструк­цию, в которой некая, идущая подряд группа действий (шагов) ал­горитма можем выполняться несколько раз, в зависимости от вход­ных данных или условия задачи. Группа повторяющихся действий на каждом шагу цикла называет­ся телом цикла. Любая цикли­ческая конструкция содержит в себе элементы ветвящейся алгоритмической конструк­ции.

Цикл с предусловием.

В данной циклической структуре сначала проверяется значение условного выражения (условие) перед выпол­нением очередного шага цикла. Если значение условного выражения истинно, исполняется тело цикла. После чего управление вновь пе­редается проверке условия и т.д. Эти действия повторяются до тех пор, пока условное выражение не примет значение ЛОЖЬ. При пер­вом же несоблюдении условия цикл завершается. Количество шагов цикла заранее не определено и зависит от входных данных задачи. Особенностью цикла с предусловием является то, что если из­начально условное выражение ложно, то тело цикла не выполнится ни разу.

	б)
Рис. 2. Блок-схема цикла с предусловием: два варианта изображения с помощью условного блока а) и с помощью блока границы цикла б)

Цикл с постусловием.

Как и в цикле с предусловием, в циклической конструкции с постусловием заранее не определено число повторений тела цикла, оно зависит от входных данных задачи. В отличие от цикла с пред­условием, тело цикла с постусловием всегда будет выполнено хотя бы один раз, после чего проверяется условие. В этой конструкции тело цикла будет выполняться до тех пор, пока значение условного выражения ложно (условие "окончания" цикла). Как только оно становится истинным, выполне­ние команды прекращается. Возможно построение цикла и с условием "продолжения" цикла, т.е. тело цикла будет выполняться до тех пор, пока значение условия истинно. Блок-схема данной конструкции пред­ставлена на рис. 3 двумя способами: с помощью условного блока а и с помощью блока управления б.

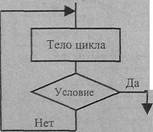
Рис. 3. Блок-схема цикла с постусловием

Рассмотрим три типа циклических алгоритмов: цикл с параметром (который называют арифметическим циклом), цикл с предусловием и цикл с постусловием (их на­зывают итерационными).

Существует разновидность цикла с предусловием, называемая арифметический цикл. В арифметическом цикле число его шагов (повторений) одно­значно определяется правилом изменения параметра, которое зада­ется с помощью начального (N) и конечного (К) значений параметра и шагом (h) его изменения. Т.е., на первом шаге цикла значение па­раметра равно N, на втором – N + h, на третьем – N + 2h и т.д. На последнем шаге цикла значение параметра не больше К, но такое, что дальнейшее его изменение приведет к значению, большему; чем К.

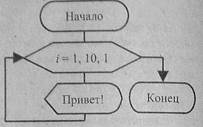
Например, вывести 10 раз слово «Привет!». Его блок-схема использует специальный блок начала арифметического цикла с указанием, что переменная i в нем будет изменяться от 1 до 10 с шагом 1.