Распределение студентов по возрасту

Тема 5. Позиционные средние: мода и медиана

Содержание задания и требования к нему

По теме 5 студент должен решить задачу, номер которой соответствует варианту.

 

Задача 1. По данным о распределении рабочих вагонного депо по заработной плате определите моду и медиану:

Заработная плата за месяц, руб.	До 5400	5400–5600	5600–5800	5800–6000	Свыше 6000	Итого
Число рабочих, чел.

Задача 2. По приведенным данным определить средний возраст группы людей (рассчитать медиану).

Возраст, лет	21–25	26–30	31–35	36–40	41–45	46–50	51–55	Итого
Численность, чел.

Задача 3. Имеются следующие данные о распределении предприятий по стоимости основных средств. Определить моду и медиану.

Стоимость ОС, млн. руб.	До 3000	3000–6000	6000–9000	9000–12000	Свыше 12000	Итого
Количество предприятий, %

Задача 4. По имеющимся данным о распределении групп рабочих по стажу работы определить медиану.

Стаж работы, лет	До 2	2–4	4–6	6–8	8 и более	Итого
Число рабочих

Задача 5. Рассчитайте моду, медиану, квартили и децили по данным о распределении магазинов по размеру товарооборота.

Группы магазинов по размеру товарооборота, тыс. руб.	Число магазинов
До 200 200–300 300–400 400–500 500–600 600–700 700–800 Свыше 800
Итого

Задача 6. С целью исследования качества деталей на предприятии проверена партия из 100 деталей. Определите моду, медиану, квартили и децили.

Группы деталей по весу, г	40–50	50–60	60–70	70–80	80–90	90–100	100–110	110–120	Итого
Число деталей

Задача 7. Вычислите моду и медиану количественного состава семей на основании следующего их распределения по числу совместно проживающих членов семьи:

Число членов семьи							Итого
Число семей, % к итогу

Задача 8. Рассчитать значения моды и медианы по данным таблицы.

Группы рабочих по выполнению норм выработки, %	До 90	90–100	100–110	110–120	120–130	130 и более	Итого
Число рабочих

Задача 9. По имеющимся данным вычислите моду, медиану и квартили.

Средняя дальность поездки, км	Число поездок
20–25 25–30 30–35 35–40 40–45 45–50
Итого

Задача 10. Имеются следующие данные о распределении заводов по расстоянию от железнодорожной станции. Определите моду и медиану.

Расстояние, км	До 3	3–6	6–9	9–12	12 и более	Итого
Число заводов

Методические указания к выполнению задания по теме 5

Модой в статистике называют значение признака, наиболее часто встречающееся в исследуемой совокупности.

Медиана – значение признака, приходящееся на середину ранжиро­ванной (упорядоченной) совокупности.

Для дискретных вариационных рядов модой будет значение варианты с наибольшей частотой. Вычисление медианы в дискретных рядах распределения имеет специфику: если такой ряд имеет нечетное число членов, то медианой будет варианта, находящаяся в середине ранжированного ряда, если четное – то медианой будет средняя арифметическая из двух значений признака, расположенных в середине ряда.

Пример. Рассчитаем моду и медиану по данным табл. 5.1.

Т а б л и ц а 5.1

Распределение студентов по возрасту

Возраст									Итого
Количество студентов, % к итогу
Накопленные частоты									–

В этом ряду распределения модой является возраст 18 лет (имеет наибольшую частоту – 25). Для определения медианы нужно подсчитать сумму накопленных частот ряда. Наращивание продолжается до получения накопленной суммы частот, впервые превышающей половину. В нашем примере сумма частот составила 100, ее половина – 50. Накопленная сумма частот ряда, впервые превысившая половину равна 58. Ей соответствует значение признака, равное 21. Таким образом, возраст студентов 21 год является медианным.

Для интервальных вариационных рядов мода определяется по формуле:

,

где – нижняя граница модального интервала;

– величина модального интервала;

– частота модального интервала;

– частота интервала, предшествующего модальному;

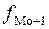– частота интервала, следующего за модальным.

Модальный интервал определяется по наибольшей частоте.

Медиана интервального ряда определяется по формуле:

,

где – нижняя граница медианного интервала;

– величина медианного интервала;

– сумма частот ряда;

– сумма накопленных частот интервала, предшествующего медианному;

– частота медианного интервала.

Пример. Рассчитаем моду и медиану по данным табл. 5.2.

Т а б л и ц а 5.2

Поделиться:

Воспользуйтесь поиском по сайту: