 |
При гармоническом источнике тока
|
|
|
|
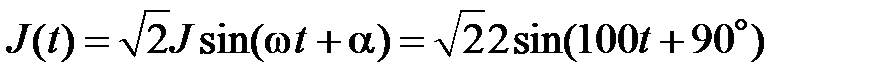 , А,
, А,
после срабатывания ключа К1 определим напряжение  .
.
2.1. Используем упрощённый классический метод, когда дифференциальное уравнение для искомой функции  не составляется.
не составляется.
2.1.1. ННУ. Определяем независимые начальные условия при  (схема до коммутации установившийся режим, гармонический источник, символический метод).
(схема до коммутации установившийся режим, гармонический источник, символический метод).
 , А; , А;
 , Ом; , Ом;
|
 ;
;
 ;
;
 .
.
Для построения графика 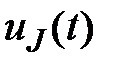 определим
определим  :
:
 , В;
, В;
 , В;
, В;
 В.
В.
2.1.2. Определяем ЗНУ при 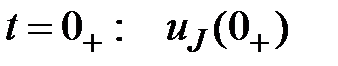 (схема после коммутации ключа К 1):
(схема после коммутации ключа К 1):
Рис. 11
 ;
;
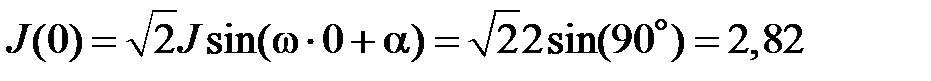 А.
А.
Используем метод контурных токов:

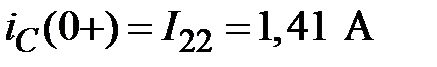 .
.
По второму закону Кирхгофа для внешнего контура

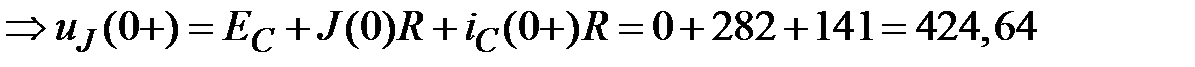 В.
В.
2.1.3. Определяем принуждённую составляющую 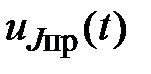 при
при  (cхема после коммутации ключа К1: установившейся режим, гармонический источник, символический метод):
(cхема после коммутации ключа К1: установившейся режим, гармонический источник, символический метод):
 , А, , А,
 , Ом. , Ом.
|
По закону Ома

Тогда
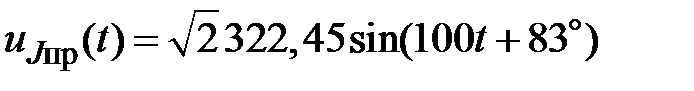 , В;
, В;
 В.
В.
2.1.4. Определяем корень характеристического уравнения 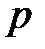 : Используем метод сопротивления цепи после коммутации. Аналогично п. 1.1.4 получаем
: Используем метод сопротивления цепи после коммутации. Аналогично п. 1.1.4 получаем 
2.1.5. Определяем постоянную интегрирования  :
:
 В.
В.
2.1.6. Окончательный результат
 , В,
, В,
причем  с – постоянная времени;
с – постоянная времени;
 с – время окончания переходного процесса;
с – время окончания переходного процесса;
 с – период принужденной составляющей.
с – период принужденной составляющей.
Заполняем таблицу для построения графика:
| t | τ | 2τ | 3τ | 4τ | 5τ | |
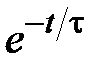
| 0,368 | 0,135 | 0,05 | 0,018 | 0,007 | |
–29,67 
| –29,67 | –10,915 | –4,015 | –1,477 | –0,543 | –0,2 |
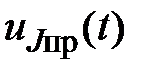 , В , В
| 452,67 | –131,838 | –337,949 | 419,11 | –10,874 | –410,06 |
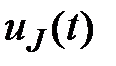 , B , B
| –148,753 | –341,964 | 417,63 | –11,417 | –410,26 |
Строим график, для построения можно использовать MathCAD.
Рис. 13
Ниже приводится расчет рассматриваемого примера в среде MathCAD.
| Документ Mathcad |

|
| Исходные данные: |

|

|

|

|

|

|
| 2.1. Классический метод, гармонический источник |

|

|
| 2.1.1. Определяем независимые начальные условия: |

|

|

|

|
| 2.1.2. Определяем зависимые начальные условия: |

|

|

|

|

|

|
| 2.1.3. Определяем принуждённую составляющую: |

|

|

|

|

|

|

|

|

|

|
|
|
|
| 2.1.4. Определяем корень характеристического уравнения: |

|

|
| 2.1.5. Определяем постоянную интегрирования: |

|

|
| 2.1.6. Окончательный результат: |

|

|
| 2.1.7. Строим график искомой фунции: |

|

|

|

|
2.2. Используем комбинированный операторно-классический метод для определения  .
.
2.2.1. Находим независимые начальные условия (п. 2.1.1):
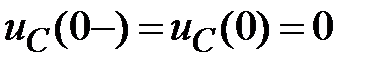 .
.
2.2.2. Определяем принуждённые составляющие  при
при  (cхема после коммутации ключа К1: установившийся режим, гармонический источник, символический метод.)
(cхема после коммутации ключа К1: установившийся режим, гармонический источник, символический метод.)
 , А; , А;
 , Ом, , Ом,
|

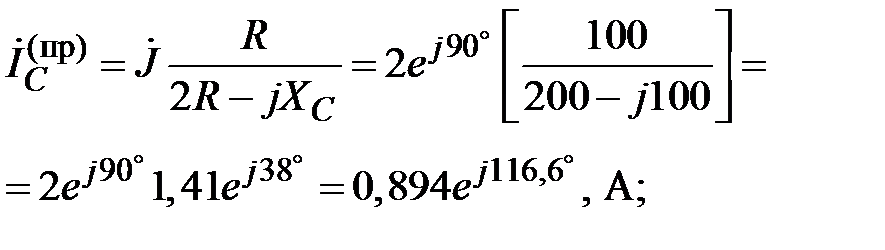

В результате

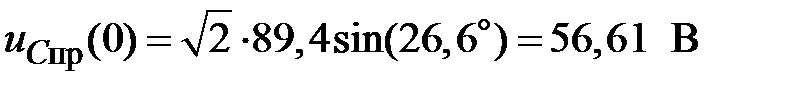 .
.
2.2.3. Определяем начальное значение свободной составляющей напряжения на ёмкости:
 .
.
2.2.4. Рассчитываем операторную схему замещения для свободных составляющих.
Рис. 15
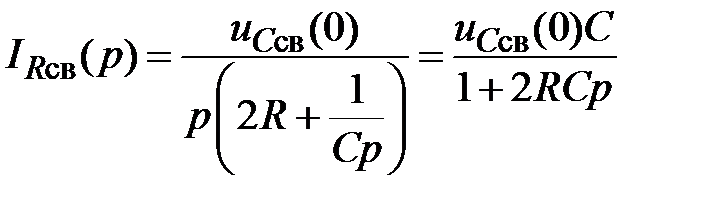 ;
;
 .
.
2.2.5. По теореме разложения и принципу наложения получаем окончательный результат
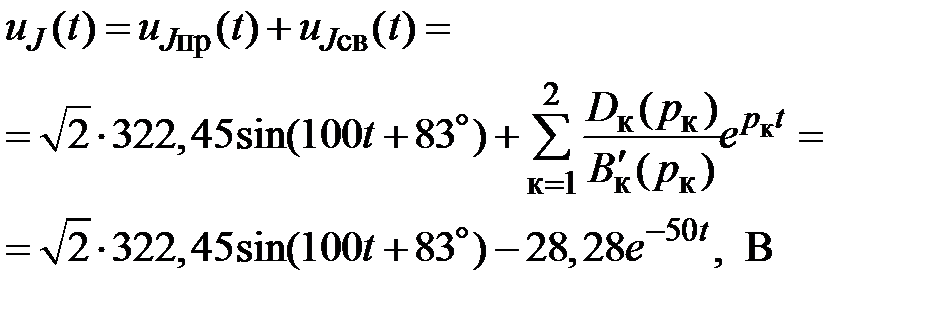
– результат практически совпал с классическим методом.
3. При импульсном источнике тока  , А (p – корень характеристического уравнения) и нулевых начальных условиях (ключ К1 сработал) определяем интегралом Дюамеля напряжение
, А (p – корень характеристического уравнения) и нулевых начальных условиях (ключ К1 сработал) определяем интегралом Дюамеля напряжение  .
.
3.1. Находим переходную характеристику h (t) для uJ (t) операторным методом при u C(0) = uC (0–) = 0.
Рис. 16
По закону Ома в операторной форме

Рис. 17
По теореме разложения находим  :
:
 ,
, 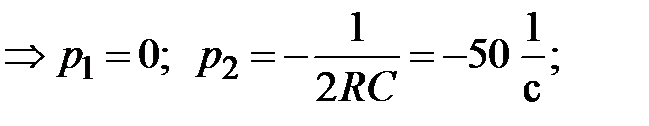
 ;
;

– переходное сопротивление.
Проверка:
а)  – верно, т.к. uC (0–) = 0 и
– верно, т.к. uC (0–) = 0 и
С – закоротка;
б) 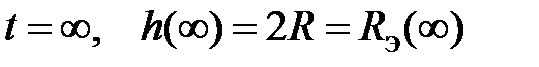 – верно, т.к. С – разрыв.
– верно, т.к. С – разрыв.
3.2. Рассчитаем интегралом Дюамеля  :
:
 ,
,
где  А;
А; 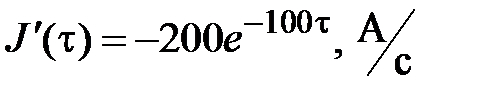 ,
,
 , Ом.
, Ом.
Тогда

Проверка:
а) 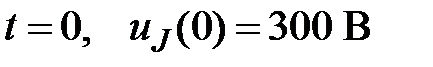 – верно, т.к.
– верно, т.к.
 В;
В;
б)  – верно, т.к.
– верно, т.к.
 .
.
3.3. Строим график  , В.
, В.
Рис. 18
Ниже приводится расчет рассматриваемого примера в среде MathCAD.
| Документ Mathcad |
|
|
|
| 3. Интеграл Дюамеля, экспоненциальный источник |

|
| 3.1. Переходная характеристика: |

|
| 3.2. Искомая функция напряжения на источнике тока: |

|

|
4. Цепь второго порядка. При постоянном источнике тока J (t) = J
после срабатывания ключа К2 определяем напряжение  . (Ключ К1 давно уже сработал).
. (Ключ К1 давно уже сработал).
4.1. Используем упрощённый классический метод, когда дифференциальное уравнение для искомой функции 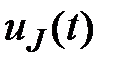 не составляется.
не составляется.
4.1.1. Определяем независимые начальные условия (ННУ): 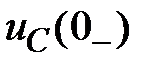 при
при  (Cхема до коммутации: установившийся режим, постоянный источник, С – разрыв, L – закоротка).
(Cхема до коммутации: установившийся режим, постоянный источник, С – разрыв, L – закоротка).
Рис. 19
Находим: 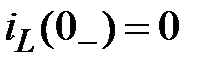 ;
;  В.
В.
Для построения графика  определим
определим  В.
В.
4.1.2. Определяем ЗНУ 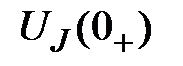 при
при 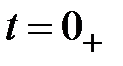 (Схема после коммутации ключа К2):
(Схема после коммутации ключа К2):
Рис. 20
 ;
;
 В – законы коммутации.
В – законы коммутации.
По законам Кирхгофа
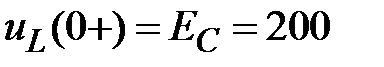 В;
В;

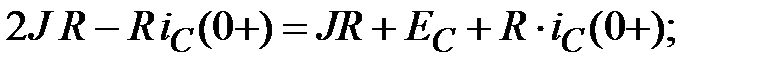
 ;
;
 В;
В;
 ;
;

Находим  .
.
Записываем уравнения по законам Кирхгофа:

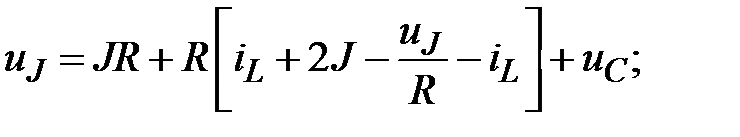

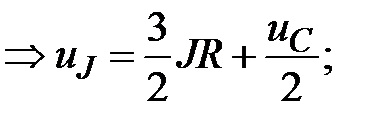


4.1.3. Определяем принуждённую составляющую 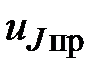 при
при  (Схема после коммутации ключа К2: установившийся режим, постоянный источник, С – разрыв, L – закоротка);
(Схема после коммутации ключа К2: установившийся режим, постоянный источник, С – разрыв, L – закоротка);
 В. В.
|
4.1.4. Определяем корень характеристического уравнения 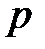 . Используем метод сопротивления цепи после коммутации:
. Используем метод сопротивления цепи после коммутации: 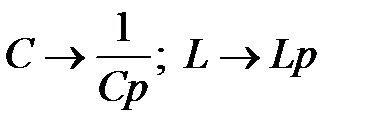 , причём
, причём  , а
, а  .
.

|
 .
.
4.1.5. Определяем постоянные интегрирования 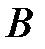 и
и  :
:
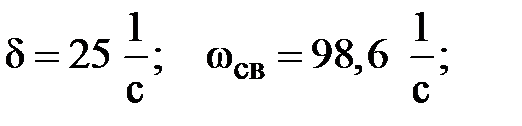
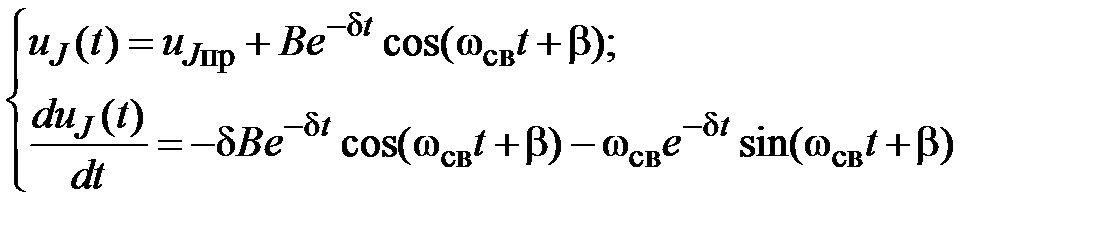
или


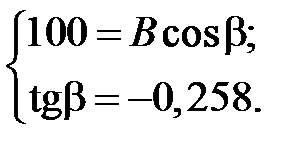

 В.
В.
4.1.6. Окончательный результат –

где 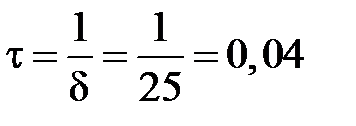 с – постоянная времени;
с – постоянная времени;
 с – длительность переходного процесса;
с – длительность переходного процесса;
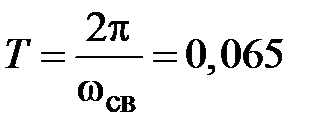 с – период свободных колебаний.
с – период свободных колебаний.
4.1.7. На интервале времени  при помощи MathCAD строим
при помощи MathCAD строим  .
.
Рис. 23
Ниже приводится расчет рассматриваемого примера в среде MathCAD.

|

|

|

|

|
| 4.1. Классический метод, постоянный источник, цепь второго порядка |
| 4.1.1. Определяем независимые начальные условия: |

|

|

|

|
| 4.1.2. Определяем зависимые начальные условия: |

|
| 4.1.3. Определяем принуждённую составляющую: |

|

|

|
| 4.1.4. Определяем корень характеристического уравнения: |

|
| 4.1.5. Определяем постоянные интегрирования: |

|

|

|

|
| 4.1.6. Окончательный результат: |

|

|

|
| Документ Mathcad |
| 4.1.7. График искомой фунции |

|

|

|

|
В результате преобразований

Т.е. результат совпадает с расчётом «вручную».
4.2. Используем операторный метод для определения  .
.
|
|
|
4.2.1. Из расчёта установившегося режима до коммутации находим независимые начальные условия (п. 4.1.1):
 ;
;  В.
В.
4.2.2. В операторной схеме после коммутации используем метод наложения:
Рис. 24
а) подсхема с источником тока  :
:
Рис. 25


б) подсхема с источником  :
:
Рис. 26

Операторное изображение искомого напряжения

4.2.3. По теореме разложения находим искомое напряжение
 :
:


 ;
;
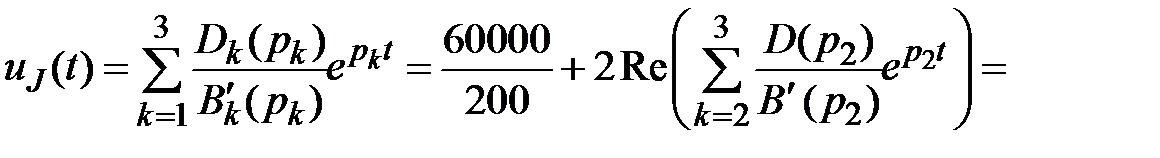
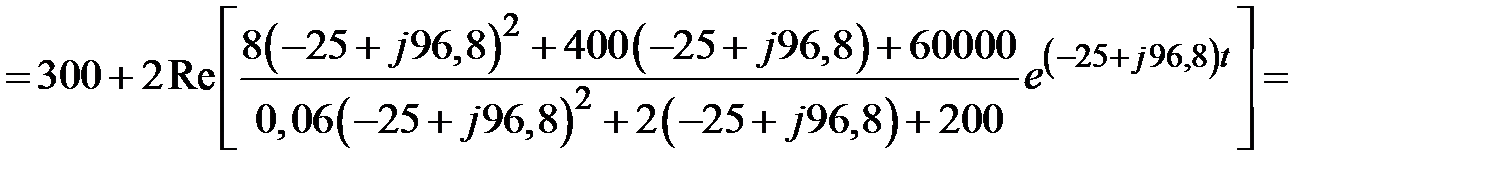

Проверка:
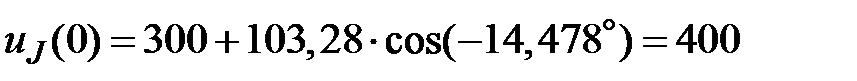 В.
В.
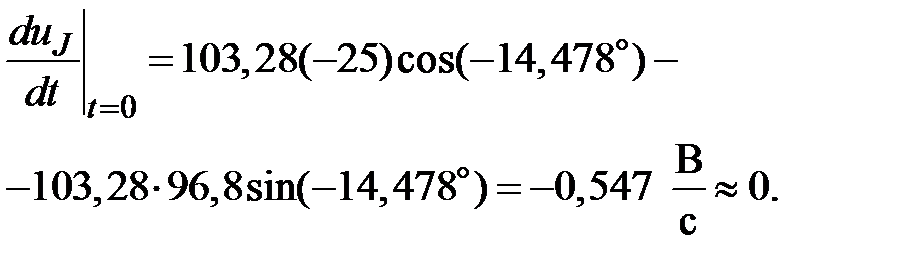
Ниже приводится расчет рассматриваемого примера программой MathCAD.
| Документ Mathcad |

|

|

|

|

|
| 4.2. Операторный метод, постоянный источник, цепь второго порядка |
| 4.2.1. Определяем независимые начальные условия: |

|

|

|

|
| 4.2.2. Определяем изображение искомой функции: |

|

|
| 4.2.3. Определяем оригинал искомой функции: |

|

|
4.3. Методом переменных состояния находим  .
.
4.3.1. Начальные условия:
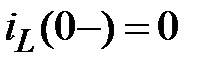 ;
; 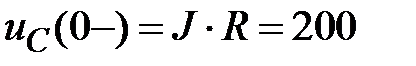 В;
В;  В.
В.
4.3.2. По законам Кирхгофа составляем уравнения
состояния:

 ;
;



4.3.3. Решаем с использованием MathCAD методом Эйлера.
Пункт 4.3.3 можно решить методом Рунге – Кутта (смотри пример п. 1.11).
| Документ Mathcad |
Полученный график полностью совпадает с уже построенной зависимостью с использованием классического и операторного методов.
|
|
|


