Электрическая цепь с последовательным соединением элементов

Билет 12

Расчет переходных процессов классическим методом в последовательной RLС – цепи.

Активные четырехполюсники.

Четырехполюсник называется активным,если внутри содержится источник электрической энергии,

 

Билет 13

Разряд конденсатора на RL – цепь при вещественных корнях характеристического уравнения.

Характеристические параметры четырехполюсников

Билет №14.

Разряд конденсатора на RL – цепь при кратных корнях характеристического уравнения.

1.

;

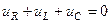
где – коэффициент затухания;

– собственная частота контура (резонансная)

Характер процессов при разряде конденсатора оказывается существенно различным в зависимости от того, будут ли корни характеристического уравнения вещественными или комплексными, что определяется соотношениями между параметрами R, L и С.

В зависимости от соотношений между параметрами цепи могут быть:
1) вещественными различными (R > 2Ö L/C);
2) вещественными равными (R = 2Ö L/C);
3) комплексно-сопряженными (R < 2Ö L/C).

В первых двух случаях переходный процесс носит апериодический характер: разрядный ток не изменяет направления в течение всего процесса; в третьем случае процесс разряда колебательный.

Апериодический разряд

Колебательный разряд

 

2. Уравнения четырехполюсника через характеристические параметры.

Четырехполюсник – часть электрической цепи, имеющая два входных и два выходных зажима(трансформатор, линия электропередачи, фильтр, электронный усилитель).

Понятием "четырехполюсник" пользуются, когда нужно знать токи и напряжения на входе и выходе электротехнического устройства и нет необходимости знать токи и напряжения внутри этого устройства.

Пассивный четырехполюсник – четырехполюсник не содержит источника энергии (активный – содержит).

Симметричный четырехполюсник – перемена местами его входных и выходных зажимов не изменяет входных и выходных напряжений и токов.

Параметры (коэффициенты) четырехполюсника () зависят от структуры (схемы внутренних соединений) четырехполюсника, величин сопротивлений элементов, составляющих четырехполюсник, и представляют в общем случае комплексные числа.

Для каждого четырехполюсника эти коэффициенты можно определить расчетным или опытным путем.

– тип (форма) А;

или

– основное уравнение четырехполюсника.

Уравнения связи между коэффициентами .

Для симметричного четырехполюсника .

–Z- форма. Уравнение связи .

–Y- форма. Уравнение связи .

–H- форма. Уравнение связи .

–G- форма. Уравнение связи .

 

 

Билет №15

1. Разряд конденсатора на RL – цепь при комплексных сопряженных корнях характеристического уравнения.

1.

;

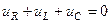
где – коэффициент затухания;

– собственная частота контура (резонансная)

Характер процессов при разряде конденсатора оказывается существенно различным в зависимости от того, будут ли корни характеристического уравнения вещественными или комплексными, что определяется соотношениями между параметрами R, L и С.

при комплексных сопряженных корнях характеристического уравнения:

 

, т.е. или .

Корни комплексно сопряженные:

;

,

где – угловая частота затухающих колебаний.

; .

Для тока:

;

; .

Процесс колебательный. Ток и напряжения на всех участках периодически меняют знак. Амплитуда колебаний убывает по показательному закону – затухающие колебания с угловой частотой ; .

При ; ; – формула Томпсона – незатухающие колебания с периодом ; – резонансная (собственная) частота контура. При этом и в цепи устанавливается режим, полностью соответствующий установившемуся процессу в нем при резонансе.

 

2. Передаточные функции согласованных цепных схем.

Билет.

1. Переходные процессы при мгновенном изменении параметров RL-цепи. Некорректные коммутации.

 

При размыкании ключа появится дуга между размыкающимися контактами (рис. 1.3), которая будет гореть до тех пор, пока токи в цепи не сравняются. При таких коммутациях должно выполняться условие равенства суммарных потокосцеплений.

 

 

 

 

При некорректной коммутации:

 

 

 

График:

 

2. Коэффициенты затухания и фазы фильтра в полосе затухания фильтров.(и в полосе пропускания тоже случайно попалось – ответ на 2 вопрос 16 билета)

 

ФНЧ

 

 

ФВЧ

 

 

Полосовой фильтр и заграждающий фильтр.

 

Билет.

1. Переходные процессы при мгновенном изменении параметров RC – цепи. Некорректные коммутации.

 

 

В случае некорректной коммутации должны быть равны суммарные заряды конденсаторов:

 

 

 

При замыкании ключа возникает дуга, которая будет гореть до тех пор, пока напряжения на конденсаторах не сравняются.

 

Суммарные заряды равны:

 

Напряжение в первый момент коммутации:

 

2. Фильтр низких частот типа К.

 

 

Билет 20

1. Полосовой фильтр типа k

2. Законы Ома и Кирхгофа в операторной форме

Билет 21

1. Методика расчета переходных процессов операторным методом

2. Заграждающий фильтр типа k

Билет 22.

 

Переход от изображения к оригиналу

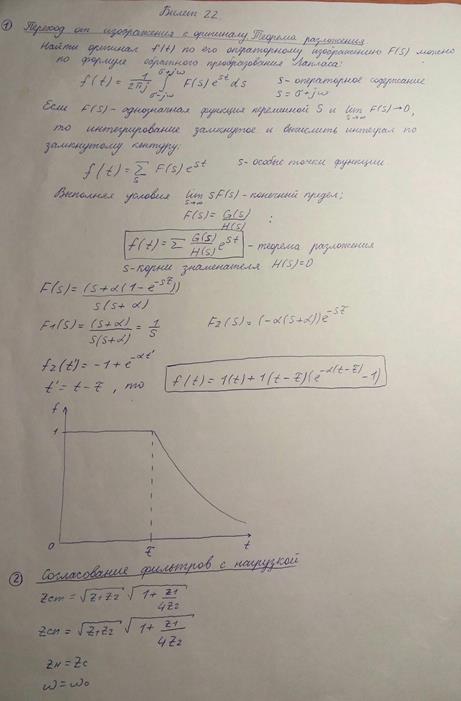
Билет 23

Представление непериодических функций времени с помощью интеграла Фурье

Билет 24.

1. Фильтры типа m.

Фильтры, электрические параметры которых получают путем пересчета параметров фильтров типа k с использованием расчетного параметра m, называют фильтрами типа m. Фильтр типа m является по существу фильтром типа k с добавлением еще одного элемента, включае­мого последовательно или параллельно. Фильтр типа М раз­рабатывают таким образом, чтобы на определенной частоте, находящейся за частотой среза f_СР, обеспечивалось (при чисто реактивных элементах) бесконечно большое ослабление сигна­ла. Импедансы элементов фильтра связаны между собой посто­янной т, зависящей от отношения частоты среза f_Ср к частоте бесконечно большого ослабления f_oo,. Значение m находится между нулем и единицей и обычно составляет 0,6. Для более острого среза величину m выбирают вблизи нуля. При m=1 фильтр является фильтром типа “К”. При малых “m” крутизна АЧХ вблизи ωС очень большая, но при более высокой частоте в полосе задержания коэффициент передачи больше, чем при больших “m”. Входное сопротивление фильтра типа “М” вблизи ωС зависит от “m”. При m=0,6 входное сопротивление наиболее равномерно в полосе пропускания.

2. Частотные характеристики токов и напряжений.

Рассмотрим зависимости напряжений и тока в контуре от частоты. Для возможности обобщенного анализа перейдем к относительным единицам, разделив их на входное напряжение при резонансе U = RI _0.

где i = I / I ₀, u _k = U_k / U, v = ω /ω ₀ - соответственно ток, напряжение и частота в относительных единицах, в которых в качестве базовых величин приняты ток I ₀, напряжение на входе U и частота ω ₀ в режиме резонанса.

Абсолютный и относительный ток в контуре равен:

Из выражений приведенных выше следует, что характер изменения всех величин при изменении частоты зависит только от добротности контура. Графическое представление их при Q =2 приведено на рис. 1 в логарифмическом (а) и линейном (б) масштабах оси абсцисс.

рис 1.

На рис. 1 кривые A (v), B (v) и C (v) соответствуют напряжению на индуктивности, емкости и резисторе или току в контуре. Кривые A (v)=u _L (v) и B (v)=u _C (v) имеют максимумы, напряжения в которых определяются выражением

,

а относительные частоты максимумов равны

При увеличении добротности Q -> ∞, A _max = B _max -> Q, а v ₁ ® 1.0 и v ₂ ® 1.0.

С уменьшением добротности максимумы кривых u _L (v) и u _С (v) смещаются от резонансной частоты, а при Q ² < 1/2 исчезают, и кривые относительных напряжений становятся монотонными.

Напряжение на резисторе и ток в контуре имеют при резонансной частоте максимум равный 1,0. Если на оси ординат отложить абсолютные значения тока или напряжения на резисторе, то для различных значений добротности они будут иметь вид, показанный на рис. 2. В целом они дают представление о характере изменения величин.

Билет 25.

1.Методика расчета переходных процессов при помощи частотных характеристик.

Принципиально отличным методом расчета переходных процессов является частотный. Он не требует составления дифференциальных уравнений цепи, а базируется на использовании интегрального преобразования Фурье. Его первый этап — нахождение спектральной плотности — Фурье-изображения входного сигнала f ₁(t).

Далее в частотной области с помощью передаточной функции находят изображение выходной величины

затем временную зависимость выходного сигнала f ₂(t) определяют с помощью обратного преобразования Фурье

При анализе переходных процессов принимают, что входное воздействие прикладывается к цепи в момент времени t = 0. С помощью интеграла Фурье можно рассматривать переходные процессы при нулевых начальных условиях, когда входное воздействие f ₁ прикладывается к цепи, не имеющей начального запаса энергии, а при t < 0 все токи и напряжения равны нулю,т.е. f ₁(t) = 0 и f ₂(t) = 0 при t < 0. При анализе таких процессов формулы прямого и обратного преобразования Фурье принимают вид:

Они определяют одностороннее преобразование Фурье. Ряд его свойств совпадает со свойствами двустороннего преобразования Фурье.

Поскольку частотный метод применяют преимущественно к цепям сложной структуры, для которых передаточную функцию, в частности, можно определить экспериментально, обратное преобразование Фурье обычно находят численным интегрированием. В этом случае целесообразно перейти от комплексной формы интеграла к вещественной форме. Свойства четности вещественной части F _в и модуля F спектральной плотности F (± j w) = F _в(w) ± jF _м(w) = F (w) e ^{± j j(w)} и нечетности мнимой части F _м и аргумента j(w) позволяют привести интеграл обратного преобразования к вещественной форме

Рассмотрим далее выражение для выходного сигнала f при ± t, то есть при t > 0 и t < 0. Из последнего интеграла получим

Так как при t < 0 f (t) = 0, из полученного выражения следует, что для одностороннего преобразования Фурье имеем

2. Статические, дифференциальные и динамические характеристики нелинейных сопротивлений.

К нелинейным относятся цепи, содержащие нелинейные элементы (НЭ), у которых параметры R,L и C зависят от напряжения U, тока I и магнитного потока Ф.

Статическое сопротивление

Динамическое сопротивление

Дифференциальное сопротивление в выбранной точке характеристики (рис.1) определяется касательной в этой точке.

Тогда тангенс угла наклона этой касательной определит дифференциальное сопротивление: r_диф = dU/dI

Как при постоянном, так и при переменном токе статические и динамические (дифференциальные) сопротивления в общем случае не равны друг другу (они могут совпадать по величине только в отдельных точках или на отдельных участках характеристики). При переходе с одного участка вольт-амперной характеристики к другому статические и динамические сопротивления не остаются постоянными.
Динамическое сопротивление используется при нахождении общего решения системы уравнений электрического равновесия цепи

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 27 _

1. Расчет переходных процессов с помощью интеграла Дюамеля.

 

2. Последовательное, параллельное и смешанное соединения нелинейных элементов постоянного тока.

Электрическая цепь с последовательным соединением элементов

Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I.

На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:

U = U ₁+ U ₂+ U ₃ или IR _экв= IR ₁+ IR ₂+ IR ₃,

R _экв= R ₁+ R ₂+ R ₃.

После этого расчет цепи сводится к определению тока I всей цепи по закону Ома

,

Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: