 |
Перевод чисел из любой системы счисления в десятичную
|
|
|
|
Алгоритм перевода чисел из любой системы счисления в десятичную.
1. Представить число в развернутой записи. При этом основание системы счисления должно быть представлено в десятичной системе счисления.
2. Найти сумму ряда. Полученное число является значением числа в десятичной системе счисления.
Пример 12. 1101,012 ® х10
1. Запишем число 1101,012 в развернутой форме: 1*23 + 1*22 + 0*21 + 1*20 + 1*2-1 + 1*2-2.
2. Найдем сумму ряда: 23 + 22 + 20 + 2-1 + 2-2 = 8 + 4 + 1 + 0,5 + 0,25 = 13,7510.
Пример 13. 0,718 ® х10
1. Запишем число 0,718 в развернутой форме: 7*8-1 + 1*8-2.
2. Найдем сумму ряда: 7*0,125 + 0,0625 = 0,937510.
Перевод чисел из двоичной системы счисления в систему счисления с основанием
q = 2n.
Алгоритм перевода двоичных чисел в систему счисления с основанием q = 2n.
1. Целую часть двоичного числа разбить справа налево, а дробную - слева направо на группы по n цифр в каждой.
2. Если в крайней левой в целой части и/или в крайней правой в дробной части группе окажется меньше n разрядов, то их надо дополнить нулями до нужного числа разрядов.
3. Рассмотреть каждую группу как n-разрядное двоичное число изаписать ее соответствующей цифрой в системе счисления с основанием =2n.
Пример 14. 1101110,00012 ® х8

1101110,00012 ® 156,048
Пример 14. 1101110,00012 ® х16

1101110,00012 ® 6Е,116
Перевод чисел из системы счисления с основанием q = 2n в двоичную систему счисления.
Алгоритм перевода чисел из системы счисления с основанием q = 2n в двоичную систему счисления.
1. Каждую цифру числа, записанного в системе счисления с основанием q = 2n, заменить ее n-разрядным эквивалентом в двоичной системе счисления.
Пример 15. 315,028 ® х2
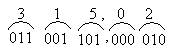
315,028 ® 11001101,000012
Пример 16. 12С16 ® х2

12С16 ® 1001011002
Двоичная арифметика
|
|
|
Таблица сложения двоичных чисел
| + | ||
| 10 |
1 означает перенос в следующий разряд
Таблица вычитания двоичных чисел
| - | ||
| 11 | ||
1 означает заем из старшего разряда
Таблица умножения двоичных чисел
| * | ||
Пример 17.
| 1101,01 + 111,10 10100,11 | 1001,10 -- 100,01 101,01 | * 101 ------ ------------- |
| Обратите внимание на то, что 1 +1 +1 = 1 + перенос 1 в следующий разряд |
Примеры из заданий ЕГЭ
1. Задание А1 демоверсии 2010 года (сайт fipi.ru)
Дано А=9D16, B=2378. Какое из чисел C, записанных в двоичной системе, отвечает условию A<C<B?
| 1) 10011010 | |
| 2) 10011110 | |
| 3) 10011111 | |
| 4) 11011110 |
Решение.
Переведем все данные нам числа в десятичную систему счисления. Проще будет сравнивать числа.
A= 9D16 = 9*161 + D*160 = 144 + 13*1 = 15710.
В = 2378 = 2*82 + 3*81 + 7*80 = 128 + 24 + 7 = 15910.
Значит, чтобы выполнялось условие A<C<B, С должно быть равно 15810. Сразу исключаем ответ под номером 3, так как это нечетное число.
Далее переведем 15810 в двоичную систему счисления. 15810 = 100111102. Правильный ответ 2.
2. Задание А4 демоверсии 2010 года (сайт fipi.ru)
Вычислите сумму чисел X и Y, если X=1101112 , Y=1358
Результат представьте в двоичном виде.
| 1) 110101002 2) 101001002 3) 100100112 4) 100101002 Решение. Переведем число Y= 1358в двоичную систему счисления. |
Y= 1358= 10111012. Выполним сложение двоичных чисел.
1 1 0 1 1 1
+ 1 0 1 1 1 0 1
-------------------
1 0 0 1 0 1 0 0 Правильный ответ 4.
3. Задание B3 демоверсии 2010 года (сайт fipi.ru)
В системе счисления с некоторым основанием десятичное число 49 записывается в виде 100. Укажите это основание.
Решение.
Допустим, что основание системы равно х, тогда составим развернутую форму записи числа:
100х = 1*x2 + 0* x1 + 0*x0 = x2.
По условию задачи х2 = 4910. Найдем х:
х2 = 49 Þ х = 7.
Можно выполнить проверку. Переведем число 4910 в 7-ричную систему счисления:
|
|
|
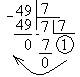
Ответ: 7.
4. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 17 оканчивается на 2.
Решение.
Последняя цифра в записи числа представляет собой остаток от деления числа на основание системы счисления 17-2 = 15. Найдем делители числа 15, это числа 3, 5,15.
Выполним проверку, записав число 17 в системах счисления с основанием 3, 5, 15:
1710 = 1223 = 325 = 1215.
Ответ: 3, 5, 15.
3. Задание B3 (Информатика: ЕГЭ-2009: Самые новые издания/ авт.-сост. О.В. Ярцева, Е.Н. Цикина. – М.: АСТ: Астрель, 2009)
В саду 100q фруктовых деревьев. Из них 33q яблони, 22q груши, 16q слив и 5q вишен. В какой системе счисления посчитаны деревья?
Решение.
По условию 33q + 22q + 16q + 5q + = 100q.
Воспользуемся развернутой формой записи чисел:
(3*q1 + 3*q0) + (2*q1 + 2*q0) + (1*q1 + 6*q0) + 5*q0 = 1*q2 + 0*q1 + 0*q0;
3q + 3 + 2q + 2 + q + 6 + 5 = q2;
q2 – 6q – 16 = 0 Þ q = 8. Проверку выполните самостоятельно.
Ответ: 8.
4. Задание B3 (Информатика: ЕГЭ-2009: Самые новые издания/ авт.-сост. О.В. Ярцева, Е.Н. Цикина. – М.: АСТ: Астрель, 2009)
(Информатика: ЕГЭ-2009: Самые новые издания/ авт.-сост. О.В. Ярцева, Е.Н. Цикина. – М.: АСТ: Астрель, 2009)
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 41, запись которых в системе счисления с основанием 3, оканчивается на 12.
Решение.
В интервале от 4 до 41 выберем те числа, которые при делении на 3 дают остаток 2. Это 5, 8, 11, 17, 20, 23, 26, 29, 32, 35, 38, 41.
Далее из полученных чисел выберем, у которых частное от их деления 3, при делении на 3 еще раз, дает остаток 1.
1) 41: 3 = 13 (ост. 2)
13: 3 = 4 (ост. 1) Þ 41 – искомое число.
2) 38: 3 = 12 (ост. 2)
12: 3 = 4 (ост. 0) – при переводе числа 38 в 3-ричную систему счисления получим число, оканчивающееся на 10, а не на 12 как нам требуется по условию задания. Не забудьте в ответе выписать полученные числа в порядке возрастания!
Ответ: 5, 14, 23, 32, 41.
5. Задание B3 (Информатика: ЕГЭ-2009: Самые новые издания/ авт.-сост. О.В. Ярцева, Е.Н. Цикина. – М.: АСТ: Астрель, 2009)
Сумму восьмеричных чисел 17 + 170 + 1 700 + … + 1 700 000 перевели в шестнадцатеричную систему счисления. Найдите в записи числа, равного этой сумме, третью цифру слева.
Решение.
Решим задание «в лоб». Найдем сумму восьмеричных чисел 17 + 170+1 700+17 000 + 170 000 + 1 700 000.

|
|
|
2 111 1078 ® х10 ® y16
2 111 1078 ® 561 73510 ® 89 2 4716.
Ответ: 2.
|
|
|


