 |
Б) как задачу булевого линейного программирования с использованием встроенной функции bintprog.
|
|
|
|
Часть 1
Постановка задач
Задача 1. Найти минимум функции f(x) при заданном векторе начальных значений переменных X0 = (x01,x02) и отсутствии ограничений. Вид функции для различных вариантов выполнения задания представлен в табл. 4.1. Найти решение данной задачи при другом (произвольном) значении X0 и сравнить его с ранее полученным решением, а также сравнить число выполненных итераций, при которых достигается решение задачи, для заданного и выбранного значеня X0.
| № варианта | Вид целевой функции | X0 | e | ||
| (1;2) | 0,25 |
Код программы:
Файл 1:
function f = myfun(x)
f = 2*x(1)^2 + 4*x(2)^2 +8*x(1)-4*x(2)+3;
2 файл:
%при первом задании значения вектора начальных значений
clc
clear
x0 = [1, 2];
[x, fval, exitflag, output] = fminunc(@myfun, x0)
Решение:
x =
-2.0000 0.5000
fval =
-6.0000
exitflag =
output =
iterations: 6
funcCount: 21
stepsize: 1
firstorderopt: 4.7684e-007
algorithm: [1x38 char]
message: [1x85 char]2й файл:
%при изменении вектора начальных значений (произвольном задании)
clc
clear
x0 = [2, 7];
[x, fval, exitflag, output] = fminunc(@myfun, x0)
x =
-2.0000 0.5000
fval =
-6.0000
exitflag =
output =
iterations: 6
funcCount: 21
stepsize: 1
firstorderopt: 1.1921e-007
algorithm: [1x38 char]
message: [1x85 char]
Полученные результаты различаются только значением firstorderopt.
Задача 2. Найти минимум функции f(x) в интервале (0, N/2), где N – номер варианта выполнения задания. Построить график минимизируемой функции и установить, совпадает ли минимальное значение функции в заданном интервале с действительным минимумом функции и если не совпадает, то визуально определить действительный минимум функции. Вид функции f(x) для различных вариантов выполнения задания представлен в табл. 4.2.
| № вари- анта | Вид функции | ||
Код программы:
Файл 1_2_5:
|
|
|
function f = myfun(x)
f = (2*x-1).^2+2;
end
2й файл:
clc
clear
[x, fval, exitflag, output] = fminbnd(@myfun, 0, 1.5)
x = 0:0.001:5.5;
y = (2*x-1).^2+2;
plot(x, y)
xlim([-1 4])
ylim([-12 40])
hold on
grid on
Полученный график:

Решение:
x =
0.5000
fval =
exitflag =
output =
iterations: 5
funcCount: 6
algorithm: [1x46 char]
message: [1x112 char]
В результате вычисления минимума функцией fminbnd и построения графика видно, что минимумы совпадают.
Задача 3. Найти минимум функции f(x) при системе ограничений G(x) и начальных значениях переменных x1(0) = 1, x2(0) = 2, x3(0) = 1. Вид функции и ограничений для различных вариантов выполнения задания представлены в табл. 4.3.
| № вари- анта | Вид функции | Ограничения | ||
Код программы:
Файл 1_3_5:
function f = myfun(x)
f = 2*x(2)^2-5*x(1)*x(2)+6*x(3)-4;
end
2й файл:
clc
clear
x0 = [1; 2; 1];
A = [3 -1 -1;
-3 1 1];
b = [0; 50];
[x, fval, exitflag, output] = fmincon(@myfun, x0, A, b)
x =
1.0e+008 *
-1.2783
-0.5609
-3.2741
fval =
-2.9558e+016
exitflag =
output =
iterations: 98
funcCount: 301
lssteplength: 2
stepsize: 2.0762e+017
algorithm: 'medium-scale: SQP, Quasi-Newton, line-search'
firstorderopt: 9.0728e+009
constrviolation: 0
message: [1x79 char]
Задача 4. Найти минимум функции f(x) при системе ограничений G(x). Вид функции и ограничений для различных вариантов выполнения задания представлен в табл. 4.4.
| № вари- анта | Вид функции 
| Ограничения 
|
Код программы:
1й файл:
clc
clear
% расчет значений по алгоритму
H = [2 -1 -4; -1 8 -2; -4 -2 -12]; %матрица Гессе
f = [5; -8; 12];
A = [-1 -1 0;0 0 -1;0 1 0]; %матрица коэффициентов левой части системы ограничений
b = [0; -6; -4]; %матрица (столбец) значений правой части системы ограничений;
[x,fval,exitflag,output] = quadprog(H, f, A, b, [],[])
Решение
x =
1.0e+016 *
2.0000
-0.0000
1.0000
fval =
-1.0000e+033
exitflag =
-3
output =
iterations: 2
algorithm: 'medium-scale: active-set'
firstorderopt: []
cgiterations: []
message: [1x96 char]
Часть 2
Постановка задачи
Найти минимум (максимум) целевой функции L(x) при ограничениях G(x), значения которых приведены в табл. 1. Решить данную задачу:
а) с помощью встроенной функции linprog, а также с помощью генетического алгоритма, используя встроенную функцию ga, и сравнить полученные результаты;
|
|
|
б) как задачу булевого линейного программирования с использованием встроенной функции bintprog.
| Номер варианта | Вид экстремума | L (x) | Ограничения |
| min | 4x1 + 10x2 + 9x3 + 3x4 | x1 - x2 - 3x3 + x4 ³ 2 x1 - x2 + x3 + 3x4 ³ 8 |
Решение задачи линейного программирования с помощью встроенной функции linprog:
Файл 2
% Решение задачи линейного программирования с помощью встроенной функции linprog
clc
clear
f = [4;10;9; 3];
A = [-1 1 3 -1; -1 1 -1 -3];
b = [-2; -8];
[x, fval, exitflag, output] = linprog(f, A, b)
x =
1.0e+015 *
-4.1402
-4.1402
-0.0000
-0.0000
fval =
-5.7963e+016
exitflag =
-3
output =
iterations: 7
algorithm: 'large-scale: interior point'
cgiterations: 0
message: [1x217 char]
Решение задачи линейного программирования с помощью встроенной функции ga:
Файл 2_2
% Решение задачи линейного программирования с помощью встроенной функции linprog
clc
clear
clc
clear
f = [4;10;9; 3];
A = [-1 1 3 -1; -1 1 -1 -3];
b = [-2; -8];
lb = zeros(4,1);
[x, fval, exitflag, output] = linprog(f, A, b,[],[],lb)
Решение:
x =
0.0000
0.0000
0.0000
2.6667
fval =
8.0000
exitflag =
output =
iterations: 8
algorithm: 'large-scale: interior point'
cgiterations: 0
message: 'Optimization terminated.'
% Решение задачи линейного программирования с помощью встроенной функции bintprog
clc
clear
f = [4;10;9; 3];
A = [-1 1 3 -1; -1 1 -1 -3];
b = [-2; -8];
lb = zeros(4,1);
[x, fval, exitflag, output] = bintprog(f, A, b, [], [], lb)
Решение:
x =
fval =
Inf
exitflag =
-2
output =
iterations: 0
nodes: 1
time: 0.5148
algorithm: 'LP-based branch-and-bound'
branchStrategy: 'maximum integer infeasibility'
nodeSrchStrategy: 'best node search'
message: 'The problem is infeasible.'
Как можно видеть, решение, полученное с помощью генетического алгоритма, является приближённым и отличается от решения, полученного на основе встроенной функции linprog.
Часть 3
ЗАДАЧА О РЮКЗАКЕ
Постановка задачи
0,1-задача о рюкзаке формулируется следующим образом. Необходимо отыскать такой набор предметов из заданного их множества с размерностью ai и стоимостью ci каждого (i = 1,…,n), которые, будучи помещёнными в рюкзак размерности A, обеспечивали бы максимальную стоимость.
Формальная постановка данной задачи имеет вид
 (1.1)
(1.1)
 (1.2)
(1.2)
В данных выражениях xi – булева переменная, при этом xi= 1,если i-й предмет кладётся в рюкзак, и xi= 0 – в противном случае.
Формулировка задания
Решить 0,1-задачу о рюкзаке. Значения весов предметов и вес рюкзака для различных вариантов выполнения задания представлены в таблице.
|
|
|
| Номер варианта | Номер предмета | Размер предмета | Стоимость предмета | Размер рюкзака |
% Задача 1
clc
clear
st = [12;11;15;8;9;6]; % ввод стоимости предмета
razm = [85 110 150 70 55 20]; % ввод размера предмета
b = 250; % размер рюкзака
[x, fval] = bintprog(-st, razm, b); % функция минимизации
x % вывод в двоичном виде
find(x==1) % номера предметов
fval = -fval % результирующая стоимость
Решение:
x =
ans =
fval =
Таким образом, как следует из полученных результатов, в рюкзак помещаются предметы с номерами 1,4, 5, 6. a их общая стоимость равна 35.
Задача 2
ЗАДАЧА О НАЗНАЧЕНИИ
Постановка задачи
Задача о назначении формулируется следующим образом.
Необходимо отыскать наилучшее – в смысле минимальной стоимости – распределение nработников по nработам при известных затратах cij, связанных с назначением работника с номером i на работу с номером j (i,j = 1,…,n).
Формальная постановка данной задачи имеет вид:
 (2.1)
(2.1)

 (2.2)
(2.2)

 (2.3)
(2.3)
В данных выражениях xij – булева переменная, которая принимает значение 1, если работник с номером i назначается на работу с номером j, и равна 0 – в противном случае.
Выражения (2.2) и (2.3) задают условия того, что каждый работник назначается только на одну работу и что на каждую работу назначается только один работник.
Формулировка задания
Решить задачу о назначении. Значения весов работ, выполняемых разными работниками, для различных вариантов выполнения задания представлены на рисунке.
| Номер варианта | Матрица соответствия весов | |||||||||||||||||||||||||||||||||||||
|
Код программы:
Файл 3_2_5:
clc
clear
f = [ 8; 7; 5; 9; 6;
5; 6; 7; 6; 7;
5; 10; 11; 9; 5;
7; 8; 9; 6; 6;
5; 6; 9; 7; 10];
A = [ 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
|
|
|
0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1;
1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0;
0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0;
0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0;
0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0;
0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1];
b = ones(10, 1);
[x,fval] = bintprog(f, [ ], [ ], A, b);
x % вывод вектора оптимальных значений
fval % общая стоимость
Решение:
Optimization terminated.
x =
fval =
Таким образом, как следует из полученных результатов, первый работник назначается на 3 работу, второй – на 2 работу, третий – на 5 работу, четвертый – на 4 и пятый работник назначается на 1 работу. Минимальные затраты, связанные назначением работников на работы, равны 27.
Задача 3
ЗАДАЧА КОММИВОЯЖЁРА
Постановка задачи
Задача коммивояжёра формулируется следующим образом.
Имеются n городов, расстояния между которыми известны. Коммивояжёр должен пройти все n городов по одному разу, вернувшись в тот город, из которого начал своё движение. Требуется найти такой маршрут движения, при котором пройденное суммарное расстояние будет минимальным.
Если считать города вершинами графа, а связи между ними – дугами графа, то задача коммивояжёра в терминах теории графов формулируется как задача отыскания кратчайшего гамильтонова цикла (контура) в полном ориентированном взвешенном графе без петель.
В формальном виде задача коммивояжёра может быть представлена следующим образом:
 (3.1)
(3.1)

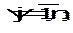 (3.2)
(3.2)

 (3.3)
(3.3)
В данных выражениях xij – булева переменная, которая принимает значение 1, если путь проходит из вершины с номером i в вершину с номером j, и равна 0 – в противном случае; cij – расстояние между i-й и j-й вершинами в графе.
Выражения (3.2) и (3.3) задают условия того, что в каждую вершину графа входит только одна дуга и что из каждой вершины выходит только одна дуга.
Следует отметить, что ограничениям (3.2), (3.3) соответствует система из нескольких меньших циклов (подциклов), которые в сумме охватывают все вершины. Чтобы устранить подциклы и всегда получать в качестве решения гамильтонов цикл, необходимо ввести дополнительные ограничения, в которых присутствуют неограниченные действительные переменные, ассоциированные с вершинами. Однако реализовать эти ограничения, оставаясь в рамках функции bintprog, невозможно, поэтому при использовании функции bintprog решение задачи коммивояжёра может быть представлено набором подциклов.
Формулировка задания
| № В. | Значения элементов матрицы расстояний | |||||||||||||||||||
| r12 | r13 | r14 | r15 | r21 | r23 | r24 | r25 | r31 | r32 | r34 | r35 | r41 | r42 | r43 | r45 | r51 | r52 | r53 | r54 | |
Решить задачу коммивояжёра. Значения весов рёбер между вершинами для различных вариантов выполнения задания представлены на рисунке.
|
|
|
Код программы:
Файл 3_3_5
clc
clear
f = [ 6; 7; 5; 7; 5;
7; 6; 8; 8; 7;
7; 5; 6; 9; 8;
7; 5; 8; 6; 5];
A = [1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1;
0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0;
1 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0;
0 1 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 0;
0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 1;
0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0];
b = ones(10,1);
[x,fval] = bintprog(f, [ ], [ ], A, b)
Решение:
x =
fval =
Таким образом, как следует из полученных результатов, оптимальным маршрутом коммивояжёра будет 1®1®4®3® 4. а его длина равна 29.
Задача 4
|
|
|


