Оборудование: Гербарные папки, альбомы, клей ПВА.

Методические указания для студентов

Перечень и тематика самостоятельных работ студентов по курсу включает освоение разделов программы и «подготовку рефератов на основе изучения основной и дополнительной литературы по предмету.

На лабораторных занятиях студенты осваивают технику создания гербария, знакомятся с методами генетического анализа. Учатся приготовлению живых и фиксированных препаратов, окрашиванию. Изучают способы количественного учета признаков. Осваивают технику статистических методов анализа.

Во время полевой практики необходимо заготовить материал и далее провести обработку. Для успешного проведения полевой практики следует составить точный календарный план работ, учитывая время, необходимое для их выполнения. Студентов целесообразно 'распределить по звеньям (по 3 — 4 человека), каждому звену заранее дать тему генетического опыта (исследования), чтобы они до начала полевых работ ознакомились с рекомендованной литературой по теме. Каждое звено отвечает полностью за проведение одного-двух исследований. С ходом проведения всех опытов (исследований) студенты знакомятся путем обзорных экскурсий.

 

Рекомендации к выполнению работ по полевой практике.

 

Работа № 1. Изучение модификационной изменчивости

Цель: Статистический анализ модификационной изменчивости признака растений по длине листовой пластинки и числу зубчиков.

Материал: Растения (клевер, лапчатки, листья деревье и др.)

Оборудование: Гербарные папки, альбомы, клей ПВА, линейки, миллиметровая бумага, калькуляторы.

Выполнение работы:

Модификационная изменчивость – это варьирование проявления признака под влиянием разнообразных условий среды. Размах модификационной изменчивости и её пределы контролируются генотипом. Этот контроль может быть жестким, вследствие чего признак варьирует в узких пределах, или наоборот, весьма пластичным, обеспечивая широкую приспособительную реакцию организма к постоянно изменяющимся условиям.

Наилучшим образом роль генотипа в определении размаха варьирования признака может отразить коэффициент вариации, большее или меньшее значение которого будет говорить о широкой или узкой норме реакции генотипа в определении данного признака.

Для исследования выбираем одну из групп близко растущих растений______ (30 шт) приблизительно одного возраста. Листья собирают с одного яруса. Каждый студент собирает по 100 листьев, готовит гербарий. Высушенные листья наклеивают на альбомные листы. Измерение длины листа производится с точностью до 1 мм, подсчет зубчиков – с точностью до единицы. Каждый студент обрабатывает свой гербарный материал.

С точки зрения методов обработки материала количественную изменчивость делят на две группы: непрерывная и прерывистая или дискретная изменчивость.

Вариации, т.е. ступени варьирования, при непрерывной изменчивости отличаются друг от друга на сколь угодно малую величину, определяемую точностью измерения. Характеризовать их можно дробными числами. Если эти числа ранжировать, т. е. располагать по порядку от меньшей к большей величине, то они составят непрерывный ряд, поэтому этот тип изменчивости получил название непрерывного. Анализируемый признак – длина листа – относится к этому типу.

Вариации при прерывистой, или дискретной, изменчивости отличаются друг от друга на целое число единиц. Число зубчиков может быть сосчитано и выражено только целым числом, поэтому варьирование по этому признаку относится к дискретному типу.

Необходимо составить вариационные ряды для каждого из изучаемых признаков. Провести статистическую обработку полученных данных, т.е. вычислить такие основные параметры модификационной изменчивости как средняя арифметическая, среднее квадратичное отклонение (стандартное отклонение), нормированное отклонение, коэффициент вариации. Построить вариационные кривые.

 

Работа № 2. Изучение множественного аллелизма по «седым» пятам у клевера белого.

Цель: проследить характер наследования рисунка седых пятен на листьях белого клевера.

Материал: Растения белого клевера.

Оборудование: Гербарные папки, альбомы, клей ПВА.

Выполнение работы.

У клевера белого (Trifolium repens) известен наследственный полиморфизм по признаку наличия – отсутствия «седого» пятна на листьях, по разнообразию формы этого пятна. Разнообразие обусловлено существованием серии неоморфных множественных аллелей гена U.

Аллель	Фенотипическое проявление
U	Пятно отсутствует
V	Полное пятно
Vh	Полное высокое пятно
Vb	Разорванное пятно
Vbh	Разорванное высокое пятно
Vp	Центральная верхняя точка
Vf	Большое сплошное пятно у основания
Vl	Низкое треугольное пятно у основания
Vm	m - образное пятно

 

Гистологические исследования показали, что пятна связаны с группой полисадных клеток, в которых хлоропласты отсутствуют или содержаться в меньшей концентрации. При этом полисадные клетки в районе пятна уменьшены в размерах, менее вытянуты, пространство между ними оказывается большим, чем в зеленой зоне листа. Сходные пятна встречаются и у других видов клевера, например у красного, где показано, что возникновение таких пятен связано с различной скоростью роста эпидермальных и полисадных клеток. Последние подвергаются больше сильному действию света, ведущего к разрушению хлорофилла. Различные уровни расположения пятен определены временем в онтогенезе, к которому приурочено действие соответствующих аллелей, нарушающих нормальное развитие хлорофилла. Аллель U рецессивная по отношению ко всем остальным аллелям. Однако для большинства комбинаций аллелей характерно их проявление совместно с образованием различных вариантов. В ряде случаев в компаунде наблюдается доминирование одной из аллелей, чаще – кодоминирование.

Для изучения полиморфизма листьев у клевера материал собирают в популяциях, произрастающих в разных местообитаниях.

Каждый студент собирает по 1-3 листа с одного растения, всего 100 листьев. Далее каждый студент изготавливает гербарий листьев белого клевера. Высушенные листья наклеивают на альбомные листы. При обработке гербарного материала определяют фенотип каждого листа, проводят анализ соотношения разных фенотипов этой серии.

Количество генотипов определяют по формуле:

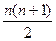, где n – количество аллелей.

Количество гомозиготных генотипов соответствует n. Количество гетерозиготных генотипов рассчитывают по формуле:

.

 

Приложение к Работе №1

 

СТАТИСТИЧЕСКИЕ МЕТОДЫ ИЗУЧЕНИЯ ИЗМЕНЧИВОСТИ

 

При изучении явлений изменчивости исследователь всегда имеет дело с совокупностью единиц — особей или их признаков. Наиболее общую или полную совокупность называют генеральной. Генеральная совокупность может включать такое большое число единиц, что изучение ее будет очень затруднено или вообще невозможно. В этих случаях для изучения используется выборочная совокупность, или выборка. Например, число растений в сортоиспытании на делянках всех повторений какого-либо сорта составляет генеральную совокупность. Для определения элементов продуктивности этого сорта нельзя проанализировать все растения, сохранившиеся на данной площади к моменту уборки урожая, поэтому берут выборку, состоящую лишь из нескольких десятков растений. Выборку составляют по принципу случайности и она должна правильно отображать генеральную совокупность. Число единиц, составляющих выборку, называется ее объемом и обозначается буквой n. Между единицами выборки всегда имеются различия, любой изучаемый признак приобретает разные значения, т. е. варьирует. Это различие между единицами совокупности называют вариацией, или дисперсией. Отдельная особь или величина изучаемого признака называется вариантой и обозначается буквой X. Минимальные и максимальные значения вариант называются лимитами. Для изучения любой совокупности особей составляют вариационный ряд, группируя по классам и последовательно располагая варианты в возрастающем или убывающем значении признака с указанием их частоты.

Число вариант в каждом классе называется частотой (f). Графическое изображение вариационного ряда дает вариационную кривую.

В качестве примера приведем вариационный ряд изменчивости числа колосков в 300 колосьях пшеницы (рис. 74):

варианты (X) 11 12 13 14 15 16 17 18 19 20 21

частота или

повторяемость вариант (F) 2 7 15 18 44 70 73 40 21 8 2

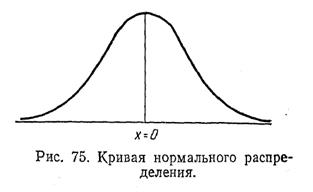
Частота отклонения отдельных вариант от средней арифмети­ческой генеральной совокупности является функцией их величин. Графически эта закономерность, основанная на законе распределения случайных величин, выражается симметричной плавной кривой, называемой кривой нормального распределения (рис. 75).

Чем ближе варианты к средней арифметической, тем чаще они встречаются, и, наоборот, чем больше варианты от нее отклоняются, тем реже они встречаются в генеральной совокупности.

Важнейшей статистической характеристикой вариационного ря­да является средняя арифметическая (я). Она представляет частное от деления всех вариант выборки на общее их число:

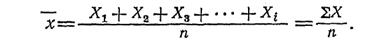
Среднюю арифметическую выражают в тех же единицах измерения, что и характеризуемый ею признак. Она дает обобщенную характеристику изучаемого признака, являясь как бы точкой равновесия, вокруг которой колеблются все его значения. Но средняя арифметическая не дает представления о характере варьирования данного признака. В самом деле, легко себе представить два вариационных ряда с одинаковыми средними арифметическими, но разным характером варьирования.

 

Основными показателями, характеризующими степень варьирования признака, служат варианса (σ²) и среднее квадратическое (стандартное) отклонение (σ). Варианса — частное от деления суммы квадратов отклонений отдельных значений вариант от средней арифметической на число степеней свободы (всех измерений без единицы) данного вариационного ряда (n— 1), а среднее квадратическое отклонение— корень квадратный из этой величины:

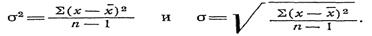
Возводя отклонения в квадрат, увеличивают значения положения данного класса в вариационном ряду. При этом чем дальше от середины ряда расположена варианта, тем более увеличивается размах ее колебания, наиболее отдаленные варианты приобретают большее значение.

Среднее квадратическое отклонение служит показателем вариабельности признака. В математической статистике доказывается, что случайная величина, распределенная по нормальному закону,практически не отклонится от генеральной совокупности более чем на ±3 σ («правило плюс — минус трех сигм»). По этому правилу в пределах ±1 σ находится 68,28% вариант выборочной совокупности, распределяющейся по закону распределения случайных величин, в пределах ±2 σ заключено 95,45%, а в пределах ±3 σ —99,73% всех вариант (рис. 76).

Определив величину среднего квадратического отклонения, вычисляют ошибку средней арифметической 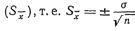для большой выборки и —для ограниченной выборки, когда объем ее n<30.

Среднее квадратическое отклонение характеризует степень разнообразия признака в выборке с определенной средней арифметической. При изучении характера варьирования признаков, выраженных в различных единицах измерения, им пользоваться нельзя. Для применения среднего квадратического отклонения в качестве меры сравнения степени варьирования признаков, выраженных разными единицами измерения, его выражают в процентах от -средней арифметической. Этот показатель, будучи величиной относительной, выражает изменчивость признаков в процентах и называется коэффициентом вариации (V).

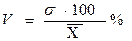
Если, например, имеются два вариационных ряда — изменчивости массы 1000 зерен и числа зерен в колосе и требуется определить, какой из этих признаков варьирует сильнее, то вычисляют, а затем сравнивают коэффициенты вариации этих рядов.

Пусть коэффициент вариации массы 1000 зерен

V= 1.35*110/30=4.5%, а коэффициент вариации числа зерен в колосе

V=2.3*100/15=16,0%. Из сопоставления этих коэффициентов вариации видно, что число зерен в колосе варьирует значительно сильнее, чем масса 1000 зерен. Теперь, зная основные статистические показатели, применяемые для изучения изменчивости, произведем анализ приведенного выше вариационного ряда по числу колосков в колосе пшеницы (табл. 14).

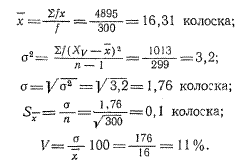
Знание и.σ, можно определить крайние значения — лимиты генеральной совокупности. Они будут находиться в пределах ±3 σ, т. е. для анализируемого вариационного ряда:

+3 σ =: 16,32+3*1,76 = 21,5 колоска;

-3 σ = 16,32—3*1,76=11,04 колоска.

Сравнение вычисленных лимитов (21,60—11,04 колоска) с лимитами анализируемой выборки (21,00—11,00 колосков) показывает, что последняя хорошо отражает генеральную совокупность.

 

Пример оформления таблицы по изменчивости признаков (изменчивости колосков в колосе пшеницы)

 

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: