 |
Уравнение предельного состояния в задачах устойчивости электропогрузчиков в пищевых производствах
|
|
|
|
Расчеты устойчивости электропогрузчика составляют значительную часть в общем объеме его проектирования, что подтверждается содержанием расчетных методик и нормативных документов. В связи с переходом на метод расчета по предельным состояниям возникает ряд проблем, связанных с обоснованием численных значений частных коэффициентов надежности. Это свидетельствует об актуальности рассматриваемой задачи.
Применительно к задачам устойчивости классические методы теории надежности сводятся либо к решению однопараметрической задачи, когда несущая способность (сопротивление опрокидыванию) принимается детерминированной, а нагрузка (или иное воздействие) случайной величиной, либо к линейной двухпараметрической. Тогда в качестве второй случайной величины в задачах устойчивости [1] выступает в большинстве случаев эксцентриситет приложения нагрузки. Решение как прямой (оценка параметров надежности), так и обратной (определение размеров опорного контура) задач первого типа трудностей не представляет практически при любом законе распределения внешнего воздействия, так как уравнение предельного состояния линейно, а точка перехода из области безотказной работы в область отказа определяется однозначно пересечением прямой, представляющей уравнение предельного состояния, с осью координат [2].
Можно значительно расширить класс решаемых задач устойчивости (сняв ограничение по линейности, увеличив количество расчетных воздействий, расширив диапазон применяемых законов распределения), если большинство преобразований в вероятностной части модели выполнять в пространстве нормированных переменных [3].
Рассмотрим нормально распределенный случайный вектор 
. При обосновании метода расчёта более целесообразно проблемы с опорными переменными рассматривать в m -мерном пространстве. Тогда каждая точка 
этого пространства есть одна реализация случайного вектора Х. Для компактности изложения перейдем к матричной форме, для чего введем вектор математических ожиданий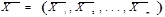 
и матрицу ковариаций
|
|
|
  … 
| ||||
| . | . | … | . | |
 ..….
| ||||
| . | . | … | . |
…  
|
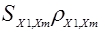
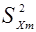
При преобразовании из исходного пространства с плотностью распределения
электропогрузчик устойчивость ненагруженный
в пространство нормированных переменных (где они становятся независимыми) с плотностью
,
где 
, необходимо главные оси довернуть до осей координат. Для этого проще всего ввести новые независимые случайные переменные 
, связанные с исходными соотношениями
и 
, (1)
где 
-ортогональная матрица, каждый столбец которой образован собственными векторами матрицы 
. Тогда матрица ковариаций автоматически приводится к диагональной форме.
Математические ожидания нормально распределенных случайных величин 
образуют вектор
. (2)
Изменчивость 
определяется матрицей ковариаций
Приведем 
к нормированному виду
С использованием зависимостей (1) и (2) получим матричное уравнение 
. (3)
Известно, что для нормированных случайных переменных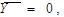 
а ковариационная матрица является единичной 
Линейное уравнение предельного состояния примем по [3]
,
где 
матрица-столбец детерминант, 
матрица-столбец детерминированных коэффициентов, а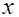 
легко получается из (3)
(4)
После подстановки в уравнение предельного состояния значение 
из (4) оно останется линейным
(5)
и посредством нормирующего множителя легко приводится к нормальному виду
|
|
|
.
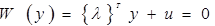Здесь
и является гарантией (уровнем) безопасности по А.Р. Ржаницыну [2], численно представляя собой квантиль нормированного нормального распределения, а
определяет пространственное положение вектора состояния, являясь своего рада коэффициентом рецептивности (чувствительности) каждого случайного переменного, определяющего надежность элемента.
В случае 
параметрической нагрузки будут иметь место соответствующие области устойчивости (безотказности) и неустойчивости (отказа) 
мерного пространства случайных переменных и поверхность предельного состояния, соответствующую критическим сочетаниям параметров нагрузки. Как отмечалось выше, форма поверхности предельного состояния зависит от структуры уравнения (5).
Решение задачи построения поверхности предельного состояния связано с итерационным процессом, для практического использования возможен и менее сложный алгоритм. Если в условие устойчивости входит несколько случайных параметров, определяющих величину опрокидывающей нагрузки, то условие устойчивости в форме (5) необходимо представить в фазовом пространстве отдельной кривой (поверхностью). При достаточно большом количестве реализаций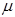 
, полученный ансамбль позволит с некоторым приближением построить функцию надежности (например, вероятности безотказной работы по критерию опрокидывания). Для произвольной точки легко подсчитать на выполненном построении количество реализаций, отделяющих ее от области отказов или безотказной работы. Если точку отделяет от области безотказной работы 
реализаций, то с известным приближением отношение 
можно считать равным вероятности отказа 
(потери устойчивости) при значениях случайных параметров, определяющих координату этой точки. Совокупность точек на плоскости (в 
мерном пространстве) с равными дает поверхность равной надежности.
Условие устойчивости при движении ненагруженного погрузчика принято в форме 
, где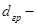 
смещение центра масс (ЦМ) погрузчика за счет уклона и центробежной силы; 
параметр опорного контура погрузчика, 
запас устойчивости.
Смещение ЦМ погрузчика при боковом наклоне на угол 
равно 
, где 
высота ЦМ погрузчика. Величина центробежной силы 
, где 
масса погрузчика без груза, 
скорость движения, 
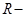радиус поворота. Равнодействующая сил, действующих на погрузчик 
, а ее отклонение от вертикали 
.
|
|
|
Смещение ЦМ погрузчика за счет боковой силы 
. Тогда суммарное смещение ЦМ 
. Стохастическое нелинейное уравнение предельного состояния по критерию опрокидывания принято в виде 
. Для решения нелинейного уравнения используется стандартный прием разложения нелинейной функции в ряд Тейлора. Если ввести вектор производных уравнения предельного состояния 
, то индекс безопасности по Корнелу - Ржаницыну можно представить в виде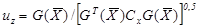 
, где 
по смыслу есть квантиль нормированного нормального распределения.
Литература
1 Собина, Л.Г., Сальников, В.В. Вероятностный подход к оценке устойчивости погрузчиков // Сб. докл. Межд. Сем. «АПИР - 7», Тула, ТулГУ, 2002. С. 159−161.
2 Ржаницын, А.Р. Теория расчета строительных конструкций на надежность. М., Стройиздат, 1978. − 239 с.
3. Сальников, В.Г., Хромов, Д.В., Чиков, К.М. Методология перехода к расчету силовых гидроцилиндров грузоподъемных машин методом частных коэффициентов надежности для линейного уравнения предельного состояния. Деп. в ВИНИТИ. №362-В98 от 10.02.98. - 30 с.
|
|
|
