 |
Перенос заряженных ионов в межзвёздном пространстве с учётом возможной конфигурации магнитных полей
|
|
|
|
В данной работе разрабатывается простейшая модель движения заряженных частиц под воздействием магнитных полей в межзвёздном пространстве с использованием аппарата дробного исчисления.
В последнее время такая интенсивно развивающаяся научная дисциплина как дробная динамика постепенно и динамично проясняет многие белые пятна в теории переноса частиц в различных средах, не говоря уже о возможности её применения и в других областях теоретической физики, как классических, так и недавно возникших (нелинейная динамика и теория хаоса). Действительно, уже не первое десятилетие в различных работах по теории переноса и странной кинетике становится всё более очевидным тот факт, что везде и всюду применяемый классический диффузионный подход к распространению частиц в различных средах, строго говоря, не совсем соответствует действительности.
Чтобы прояснить данный факт более конкретно, рассмотрим следующий пример.
Предположим, что распределение частиц по координатам 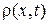 в момент времени t подчиняется диффузионному уравнению
в момент времени t подчиняется диффузионному уравнению
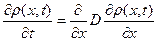 . (1)
. (1)
Положим в начальный момент времени
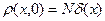 , (2)
, (2)
где δ(х) – дельта-функция Дирака.
Решение уравнения (1) с учётом начального условия (2) будет иметь вид гауссового распределения, постепенно расползающегося со временем:
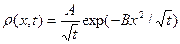 , (3)
, (3)
где коэффициенты A и В находятся подстановкой (3) в (1) с учётом условия нормировки
 .
.
Найдём квадрат среднего расстояния  , на которое частицы могли бы удалиться по стечению времени t. По определению
, на которое частицы могли бы удалиться по стечению времени t. По определению
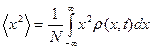 . (4)
. (4)
Подставляя соотношение (3) в (4), находим
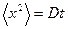 (5)
(5)
Таким образом, в классическом диффузионном приближении получаем прямую пропорциональность между средним квадратом перемещения частицы и временем её движения, причём, что самое интересное, вне зависимости от значения коэффициента диффузии D.
|
|
|
Из многочисленных экспериментов стало понятным, что более точная зависимость квадрата перемещения от времени для кинетики частиц в большинстве случаев имеет вид
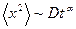 , (6)
, (6)
где α – коэффициент, зависящий от специфики среды, в которой распространяется частица. Как было впоследствии выяснено, одни процессы распространения частиц оказались более быстрыми, чем диффузионные, то есть α > 1 и их условно назвали супердиффузионными (скажем, распространение запахов одеколона в воздухе), другие же наоборот – более медленными, для которых α < 1 (взаимопроникновение молекул двух сжатых под давлением металлических пластин). Последние были названы процессами субдиффузионными.
Наиболее трудным частным случаем оказался процесс распространения заряженных частиц в среде или хотя бы даже в вакууме с учётом влияния на них и специфики конфигурации внешних магнитных полей, особенно если учесть возможность многочисленных нелинейных процессов, известных из электродинамики сплошных сред и физики плазмы. Достаточно хотя бы упомянуть возможность магнитных ловушек или зеркал, не рассматриваемых в классической теории переноса, но очевидно, имеющих существенное влияние на движение пробного заряда. Отсюда становится просто очевидным необходимость применения аппарата дробной динамики для подобного рода процессов в теории переноса частиц в случае, если это вообще возможно.
Возвращаясь к проблеме распространения заряженных частиц в межзвёздных средах с учётом влияния магнитных полей, упомянём следующий факт.
В запутанном магнитном поле траектория отдельной частицы космических лучей похожа на движение типа броуновского. Однако для частиц достаточно большой энергии ларморовский радиус, по которому частицы должны были б закручиваться под действием магнитного поля, оказывается достаточно большим и частицы уже не чувствуют магнитное поле. В последнем же случае частицы движутся практически прямолинейно. При этом интересен тот факт, что если в первом случае используют для плотности потока частиц (вдоль некоторой оси Ох, направленной вдоль преимущественного движения частиц) диффузионное приближение тип  , то во втором случае полагают
, то во втором случае полагают 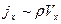 . Однако становится очевидным что как в первом, так и во втором случае подобного рода приближения, строго говоря, оказываются не соответствующими действительности.
. Однако становится очевидным что как в первом, так и во втором случае подобного рода приближения, строго говоря, оказываются не соответствующими действительности.
|
|
|
Поэтому в данном случае согласно методу дробной динамики логичнее всего было бы положить, очевидно, для плотности потока
 , (7)
, (7)
где α меняется от 0 до 1.
И тогда обобщённое уравнение диффузии приобретёт вид
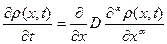 . (8)
. (8)
Из вида соотношений (7) и (8) можно определить задачу данной работы как нахождение коэффициента диффузии D и порядка дробного дифференцирования α в зависимости от конфигурации и величины внешнего магнитного поля.
Рассмотрим простейшие случаи из электродинамики и физики плазмы. Пусть однородное магнитное поле направлено вдоль движения частицы. Так как векторы скорости частиц и магнитного поля сонаправлены, то сила Лоренца со стороны магнитного поля, действующая на частицы, равна нулю. И тогда плотность потока частиц, имеющих постоянную скорость, будет определяться соотношением  , где ось Ох направлена вдоль магнитного поля.
, где ось Ох направлена вдоль магнитного поля.
Если вектор магнитной индукции поля перпендикулярен движению частиц, то частицы начинают закручиваться вокруг направления магнитного поля, причём ларморовский радиус окружности R, определяемый как
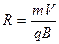 .
.
Направим ось Ох вдоль начального движения частиц. Тогда
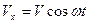 ,
,
где циклическая частота ω будет иметь вид
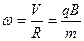 .
.
Координата x:
 + х 0.
+ х 0.
И тогда фазовая траектория в плоскости (x, Vx) будет представлять окружность
(x ω)2+ Vx 2= V 2. (9)
При усреднении по времени (или координате) соотношения (9) имеем  , откуда поток частиц
, откуда поток частиц  .
.
Таким образом, поток частиц поперёк магнитного поля (при отсутствии других полей) будет равен нулю. Иными словами, заряженные частицы оказываются как бы «вмороженными», имея возможность двигаться только вдоль силовых линий магнитного поля, но не поперёк.
|
|
|
|
|
|


