 |
Какие допущения приняты при использовании теории линейно деформируемых тел (теории упругости) при определении напряжений в грунтах?
|
|
|
|
Для того чтобы можно было воспользоваться решениями задач, имеющимися в теории упругости, приняты следующие положения:
1. Грунт состоит обычно из трех компонентов: минерального скелета, воды и воздуха, однако возможно его рассматривать как квазисплошное тело, то есть тело, имеющее свойства сплошного однородного тела, в котором трещины и пустоты отсутствуют.
Грунт можно рассматривать как тело изотропное, обладающее одинаковыми деформационными свойствами в разных направлениях.
2. Для грунта характерно наличие остаточных деформаций. При полном снятии нагрузки все деформации не исчезают, а упругие (то есть восстанавливающийся) бывают часто значительно меньше неупругих (остаточных) деформаций. Поэтому в теории линейно деформируемых тел рассматривается только процесс нагрузки, а процесс разгрузки, если в том есть необходимость, рассматривается особо.
3. Считается, что нагрузки на грунт не вызывают его разрушения и далеки от предельных; поэтому в грунтовом массиве не возникает трещин, разрывов, срезов и т.д., то есть не нарушается "квазисплошность".
4. Связь между полными напряжениями и общими деформациями принимается линейной. Таким образом, считается справедливым закон Гука, связывающий напряжения и деформации. Деформации считаются малыми.
18 Как определить сжимающие напряжения в массиве грунта с помощью таблиц (СНиП 2.02.01-83*). Какие решения положены в основу этих расчетов?
Имеем фундамент шириной b и длинной l, который оказывает на грунт давление Р:
Рассмотрим два случая приложения нагрузки (центральная и угловая):
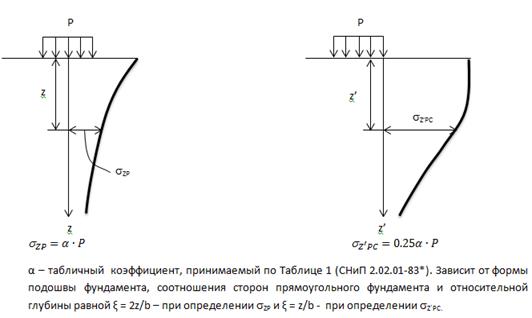
Как вычисляются вертикальные напряжения от собственного веса грунта? Начертите эпюры распределения вертикальных напряжений от собственного веса грунта для различных случаев (однородного массива, слоистого массива, при наличии в массиве уровня подземных вод и водонепроницаемого слоя).
|
|
|
Вертикальное напряжение от собственного веса грунта s z представляет собой вес столба грунта над рассматриваемой точкой с площадью поперечного сечения, равной единице. Таким образом, если в точке M на глубине z грунт однородный, получаем s z = g z; если имеются различные слои (рис.М.6.2), то
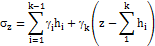
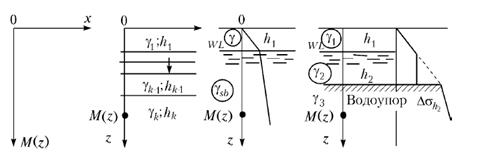
Рис.М.6.2. Определение давления в грунте
от его собственного веса и наличия уровня
грунтовой воды
Удельный вес грунта ниже горизонта воды принимается с учетом действия выталкивающей силы за счет взвешивания в воде, поэтому получаем:
sZ = g1 h1 + γsb(z – h1) = (γ – γW) z + γW h1
Давление s z в водоупорном слоепринимает ся с учетом полного веса водонасыщенного грунта (то есть выталкивающая сила не учитывается), который расположен выше данного слоя:
sz = γ1 h1 + γ2 h2 + γ3 [z – (h1 + h2]
На границе водоупора в эпюре σ z имеет место скачок на величину ∆s2h2 = g w h 2, причем в данном случае g2 = γ1 − γw.
20 Как определить напряжения по методу угловых точек, пользуясь таблицами (СНиП 2.02.01-83*).
Для определения вертикального напряжения sz в любой точке полупространства можно воспользоваться выражением szр = 0,25ꭤР.
(a) (б)


Если проекция рассматриваемой точки Мˈ на горизонтальную поверхность полупространства (точка М) располагается в пределах площади загружения (а), то эту площад можно разбить на 4 прямоугольник (1 – abMh, 2 – bcdM, 3 – Mdef, 4 – hMfg) так, чтобы точка М была угловой точкой каждого из них. Тогда напряжение szр найдём суммированием напряжений под угловыми точками четырёх площадей загружения:
Ϭzр = Ϭzс1 + Ϭzс2 + Ϭzс3 + Ϭzс4 = 0,25(ꭤ1+ꭤ2+ꭤ3+ꭤ4)P,
где ꭤ1,ꭤ2,ꭤ3,ꭤ4 – коэффициенты, принимаемые по таблице из СНиПа 2.02.01-83* в зависимости от отношения сторон площадей загружения 1,2,3,4 и отношения z (глубины расположения точки Мˈ) к ширине каждой из этих площадей.
|
|
|
Когда проекция точки Мˈна горизонтальную поверхность полупространства (точка М) располагается вне пределов площади загружения (б), точку М аналогично можно представить как угловую точку фиктивных площадей загружения 1,2,3,4 (acMf, bcMe, gdMf, hdMe). При этом в пределах площадей 2 и 3 фиктивная нагрузка прикладывается в обратном направлении. Напряжение определяется следующим образом:
Ϭzр = Ϭzс1 - Ϭzс2 - Ϭzс3 + Ϭzс4 = 0,25(ꭤ1-ꭤ2-ꭤ3+ꭤ4)Р
|
|
|


