 |
Как выразить характеристические параметры четырехполюсника через А-параметры.
|
|
|
|
Для симметричного четырехполюсника A 11 = A 22, то оба характеристических сопротивления становятся равными друг другу: Zc 11 = Zc 22 = Zc =  . Входное сопротивление симметричного четырехполюсника, нагруженного на характеристическое сопротивление Zc, равно этому сопротивлению — сопротивление согласованной нагрузки как бы повторяется на входе четырехполюсника. Поэтому характеристическое сопротивление симметричного четырехполюсника называют также повторным.
. Входное сопротивление симметричного четырехполюсника, нагруженного на характеристическое сопротивление Zc, равно этому сопротивлению — сопротивление согласованной нагрузки как бы повторяется на входе четырехполюсника. Поэтому характеристическое сопротивление симметричного четырехполюсника называют также повторным.
Уравнения симметричного четырехполюсника принимают вид:
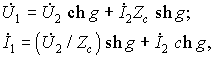
а выражения для коэффициентов KU и KI равны друг другу

и поэтому мера передачи симметричного четырехполюсника допускает наглядное истолкование
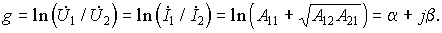
Вещественная часть меры передачи a — коэффициент затухания — определяет уменьшение действующих значений напряжения или тока при переходе от входных к выходным зажимам четырехполюсника при согласованной нагрузке. Мнимая часть b — коэффициент фазы — определяет изменение фазы тока и напряжения при переходе через согласованно нагруженный четырехполюсник b = y1 – y2. На практике затухание сигналов при переходе через четырехполюсник оценивается в децибелах и выражается через десятичные логарифмы:
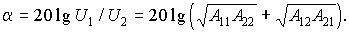
Пример. Определим характеристические параметры симметричного четырехполюсника рис. 12.12, а.

Рис. 12.12
При холостом ходе сопротивления Z 1 и Z 0 в выходной цепи включены последовательно и оба параллельны сопротивлению Z 0 во входной цепи. Таким образом, для входного сопротивления имеем:

Аналогично при коротком замыкании на выходе сопротивления Z 2 и Z 0 выходной ветви соединены параллельно, а Z 0 входной ветви — последовательно с ними. Цепочка из указанных трех сопротивлений параллельна Z 1. В результате запишем
|
|
|
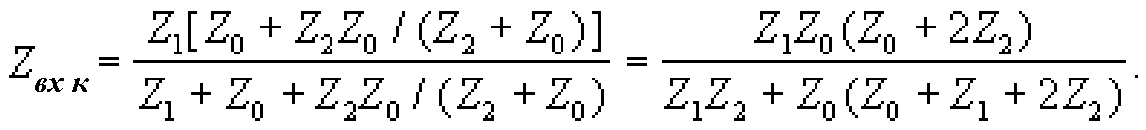
Используя оба выражения, определим характеристическое сопротивление цепи как 
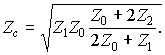
Если ее сопротивления связаны дополнительно условием: Z 1 Z 2 =  , то Zc = Z 0, а g = ln
, то Zc = Z 0, а g = ln  .
.
Для перехода к симметричной Т-образной схеме (рис. 12.12, б) в полученных соотношениях следует положить Z 1 = ¥. Имеем:
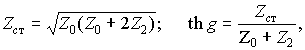 или
или 
откуда

Для перехода к симметричной П-образной схеме (рис. 12.12, в) в общих выражениях следует принять Z 2 = 0. При этом:
 или
или 
откуда

Пример:
Задача 11.3. Определить характеристические параметры четырехполюсника, рассмотренного в задаче 11.1, принимая в качестве элементов схемы Z 1 = 1/ jωC, Z 2 = jωL. Для характеристических сопротивлений справедливы следующие выражения через А -параметры (см. п. 12.7)
 .
.
Подстановка полученных в задаче 11.1. выражений А -параметров с учетом характера элементов дает 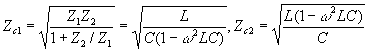 .
.
Для меры передачи четырехполюсника имеем
 .
.
Из полученных выражений следует, что при  оба характеристических сопротивления вещественны, а мера передачи — чисто мнимая величина g = jβ. При
оба характеристических сопротивления вещественны, а мера передачи — чисто мнимая величина g = jβ. При  , наоборот, характеристические сопротивления — мнимые, а мера передачи имеет ненулевую вещественную часть.
, наоборот, характеристические сопротивления — мнимые, а мера передачи имеет ненулевую вещественную часть.
 ,
эквивалентная схема:
,
эквивалентная схема:
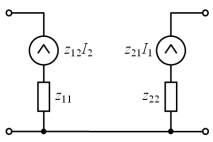 измерение параметров:
измерение параметров:
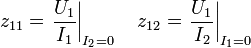
 Простейшие четырехполюсники представляют собой одноэлементные четырехполюсники, состоящие из последовательного (рис. 10.14а) или параллельного (рис. 10.14б) двухполюсника:
Простейшие четырехполюсники представляют собой одноэлементные четырехполюсники, состоящие из последовательного (рис. 10.14а) или параллельного (рис. 10.14б) двухполюсника:
 а) б)
Рис. 10.14. Одноэлементные четырехполюсники с последовательной (а) или параллельной (б) ветвью.
Уравнения четырехполюсников в форме [A]:
а) б)
Рис. 10.14. Одноэлементные четырехполюсники с последовательной (а) или параллельной (б) ветвью.
Уравнения четырехполюсников в форме [A]:
 Если в первом четырехполюснике положить
Если в первом четырехполюснике положить  или во втором
или во втором  , то получится уравнение в форме [A]:
, то получится уравнение в форме [A]:
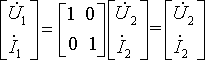 соответствующее непосредственному прямому соединению (рис. 10.15)
соответствующее непосредственному прямому соединению (рис. 10.15)
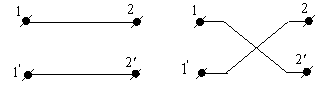 Рис. 10.15. Соединения – прямое (а) и перекрещенное (б).
Перекрещенному соединению (рис.10.15б) соответствует уравнение формы [A]:
Рис. 10.15. Соединения – прямое (а) и перекрещенное (б).
Перекрещенному соединению (рис.10.15б) соответствует уравнение формы [A]:
 Поэтому при перекрещивании входных или выходных зажимов любого четырехполюсника его матрица [A] умножается на
Поэтому при перекрещивании входных или выходных зажимов любого четырехполюсника его матрица [A] умножается на  , что равносильно замене знаков коэффициентов А.
26.Расскажите об операторном методе расчета переходных процессов. Рассмотрите включение последовательной RL цепочки на постоянное напряжение операторным методом.
ОПЕРАТОРНЫЙ МЕТОД РАСЧЁТА ПЕРЕХОДНЫХ ПРОЦЕССОВ.
Электрическая величина в цепи, содержащей реактивные элементы может быть описана обыкновенным линейным дифференциальным уравнением n–ого порядка с постоянными коэффициентами вида
, что равносильно замене знаков коэффициентов А.
26.Расскажите об операторном методе расчета переходных процессов. Рассмотрите включение последовательной RL цепочки на постоянное напряжение операторным методом.
ОПЕРАТОРНЫЙ МЕТОД РАСЧЁТА ПЕРЕХОДНЫХ ПРОЦЕССОВ.
Электрическая величина в цепи, содержащей реактивные элементы может быть описана обыкновенным линейным дифференциальным уравнением n–ого порядка с постоянными коэффициентами вида
 (2.1)
Для его однозначного разрешения должны быть определены n начальных условий (НУ) (2.2):
(2.1)
Для его однозначного разрешения должны быть определены n начальных условий (НУ) (2.2):

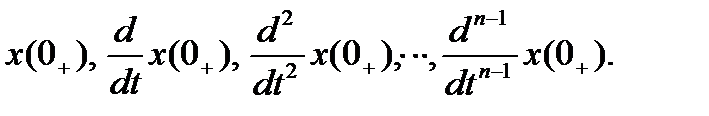 (2.2)
Кроме классического метода решения этого уравнения существует операторный метод. Суть операторного метода заключается в применении к уравнению (2.1) преобразования Лапласа:
(2.2)
Кроме классического метода решения этого уравнения существует операторный метод. Суть операторного метода заключается в применении к уравнению (2.1) преобразования Лапласа: 
 , где
, где 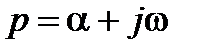 . (2.3)
Принято говорить так, что над оригиналом x(t) - функцией действительного переменного t произведена операция отображения в область комплексного переменного p. X(p)-изображение функции x(t). С целью более простой записи, в место выражения (2.3), используют специальные символы:
. (2.3)
Принято говорить так, что над оригиналом x(t) - функцией действительного переменного t произведена операция отображения в область комплексного переменного p. X(p)-изображение функции x(t). С целью более простой записи, в место выражения (2.3), используют специальные символы:  или
или 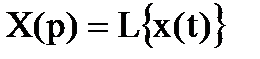 . Так, например, если применить формулу (2.3) к уравнению (2.1), то получим алгебраическое уравнение в области изображений
. Так, например, если применить формулу (2.3) к уравнению (2.1), то получим алгебраическое уравнение в области изображений
 (2.4)
Выражая из (2.4) изображение искомой величины мы получим дробно-рациональную функцию равную отношению полиномов
(2.4)
Выражая из (2.4) изображение искомой величины мы получим дробно-рациональную функцию равную отношению полиномов
 (2.5)
Решение уравнения (2.1) находится путём вычисления обратного преобразования Лапласа над отношением полиномов (2.5) по формуле
(2.5)
Решение уравнения (2.1) находится путём вычисления обратного преобразования Лапласа над отношением полиномов (2.5) по формуле
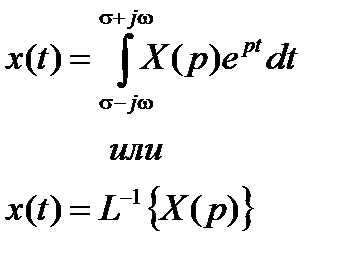 Алгоритм расчета переходного процесса операторным методом.
Из расчета цепи до коммутации находим ННУ.
Составляем операторную схему замещения цепи после коммутации.
Любым известным методом расчёта (МКТ, МУП и др.) находим изображение искомой величины в виде отношения полиномов.
От изображения переходим к оригиналу, применяя теорему разложения.
Пример расчета
Алгоритм расчета переходного процесса операторным методом.
Из расчета цепи до коммутации находим ННУ.
Составляем операторную схему замещения цепи после коммутации.
Любым известным методом расчёта (МКТ, МУП и др.) находим изображение искомой величины в виде отношения полиномов.
От изображения переходим к оригиналу, применяя теорему разложения.
Пример расчета
 ННУ ток в индуктивности в цепи до замыкания был равен нулю i(0_)=0.
Строим операторную схему замещения цепи после замыкания.
ННУ ток в индуктивности в цепи до замыкания был равен нулю i(0_)=0.
Строим операторную схему замещения цепи после замыкания.
 По закону Ома найдем операторный ток.
По закону Ома найдем операторный ток.
 Замечание: Наличие нулевого корня характеристического полинома однозначно указывает на наличие постоянной составляющей в оригинале.
Переходим от изображения к оригиналу тока.
Замечание: Наличие нулевого корня характеристического полинома однозначно указывает на наличие постоянной составляющей в оригинале.
Переходим от изображения к оригиналу тока.
 .
Используя свойство линейности преобразования Лапласа, найдём изображение каждого слагаемого в отдельности.
.
Используя свойство линейности преобразования Лапласа, найдём изображение каждого слагаемого в отдельности.

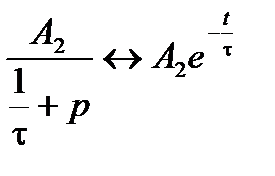 ,
где коэффициенты находим по формуле (2.8)
,
где коэффициенты находим по формуле (2.8)


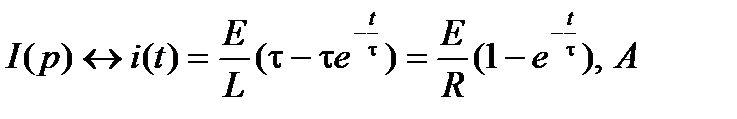 .
.
 с указанием стрелочкой вида коммутации (замыкание, размыкание) и момента времени.
Ключ считается идеальным элементом. Сопротивление ключа в открытом состоянии принимается равным нулю, а закрытом – бесконечности. Время коммутации есть бесконечно малая величина, то есть переход из одного состояния в другое происходит мгновенно.
Момент коммутации является границей между, так называемыми, до коммутационным (предшествующим) и переходным процессами (ПП). Теоретически переходный процесс длится бесконечно долго, но на практике это время считают конечным в силу затухающего характера переходного процесса. Во время переходного процесса электрическая величина стремится к некоторому установившемуся значению, по достижению которого с точностью до 99%, переходный процесс считают закончившимся. Дальнейшее состояние цепи называют установившимся процессом.
с указанием стрелочкой вида коммутации (замыкание, размыкание) и момента времени.
Ключ считается идеальным элементом. Сопротивление ключа в открытом состоянии принимается равным нулю, а закрытом – бесконечности. Время коммутации есть бесконечно малая величина, то есть переход из одного состояния в другое происходит мгновенно.
Момент коммутации является границей между, так называемыми, до коммутационным (предшествующим) и переходным процессами (ПП). Теоретически переходный процесс длится бесконечно долго, но на практике это время считают конечным в силу затухающего характера переходного процесса. Во время переходного процесса электрическая величина стремится к некоторому установившемуся значению, по достижению которого с точностью до 99%, переходный процесс считают закончившимся. Дальнейшее состояние цепи называют установившимся процессом.
 Рис. 1.1
Учет переходных процессов при проектировании и эксплуатации электротехнических устройств, как правило, обязателен. Например, в момент пуска двигателя в его обмотках могут возникать пусковые токи в несколько раз превышающие номинальные токи. Возможны в цепях и коммутационные перенапряжения, способные вызвать пробой изоляции, и как следствие, короткое замыкание.
Расчет переходных процессов основывается на решении (интегрировании) дифференциального уравнения, которым искомая величина (ток, напряжение, потокосцепление, заряд) связана с независимой переменной t – временем. Это уравнение получается из системы интегро-дифференциальных уравнений, которыми можно описать цепь по законам Кирхгофа. Оно называется линейным обыкновенным неоднородным дифференциальным уравнением (ОДУ) n-го порядка с постоянными коэффициентами вида
Рис. 1.1
Учет переходных процессов при проектировании и эксплуатации электротехнических устройств, как правило, обязателен. Например, в момент пуска двигателя в его обмотках могут возникать пусковые токи в несколько раз превышающие номинальные токи. Возможны в цепях и коммутационные перенапряжения, способные вызвать пробой изоляции, и как следствие, короткое замыкание.
Расчет переходных процессов основывается на решении (интегрировании) дифференциального уравнения, которым искомая величина (ток, напряжение, потокосцепление, заряд) связана с независимой переменной t – временем. Это уравнение получается из системы интегро-дифференциальных уравнений, которыми можно описать цепь по законам Кирхгофа. Оно называется линейным обыкновенным неоднородным дифференциальным уравнением (ОДУ) n-го порядка с постоянными коэффициентами вида
 (1.1)
Для его однозначного разрешения должны быть определены n начальных условий (НУ) (1.2), которым удовлетворяют постоянные интегрирования:
(1.1)
Для его однозначного разрешения должны быть определены n начальных условий (НУ) (1.2), которым удовлетворяют постоянные интегрирования: 
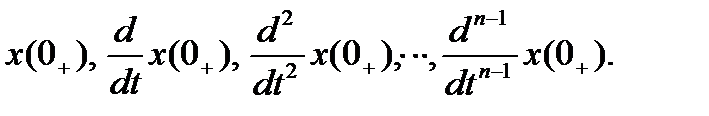 (1.2)
Из теории дифференциальных уравнений мы знаем, что решением уравнения (1.1) является сумма его частного решения для
(1.2)
Из теории дифференциальных уравнений мы знаем, что решением уравнения (1.1) является сумма его частного решения для  и общего решения однородного дифференциального уравнения вида
и общего решения однородного дифференциального уравнения вида  (1.3)
Частное решение уравнения (1.1) называют установившейся или “принуждённой” составляющей, а решение уравнения (1.3) называют свободной составляющей
(1.3)
Частное решение уравнения (1.1) называют установившейся или “принуждённой” составляющей, а решение уравнения (1.3) называют свободной составляющей
 (1.4)
Ток свободной составляющей переходного процесса обусловлен разницей энергий реактивных элементов до коммутации и в установившемся режиме. Ток принужденной составляющей обусловлен действием источников в цепи после коммутации.
КЛАССИЧЕСКИЙ МЕТОД РАСЧЁТА ПП.
Выбираем положительные направления токов в ветвях схемы.
Из расчета цепи до коммутации определяем ННУ.
Записываем искомую величину как сумму свободной и установившейся составляющих
(1.4)
Ток свободной составляющей переходного процесса обусловлен разницей энергий реактивных элементов до коммутации и в установившемся режиме. Ток принужденной составляющей обусловлен действием источников в цепи после коммутации.
КЛАССИЧЕСКИЙ МЕТОД РАСЧЁТА ПП.
Выбираем положительные направления токов в ветвях схемы.
Из расчета цепи до коммутации определяем ННУ.
Записываем искомую величину как сумму свободной и установившейся составляющих  .
Любым известным методом расчитываем установившийся режим в цепи после коммутации.
Составляем характеристическое уравнение.
.
Любым известным методом расчитываем установившийся режим в цепи после коммутации.
Составляем характеристическое уравнение.
 ;
Находим корни характеристического уравнения и по их виду записываем общее решение однородного дифференциального уравнения, т.е. общий вид свободной составляющей
;
Находим корни характеристического уравнения и по их виду записываем общее решение однородного дифференциального уравнения, т.е. общий вид свободной составляющей 
 , (1.5)
где n-порядок цепи (кол-во корней характеристического уравнения);
, (1.5)
где n-порядок цепи (кол-во корней характеристического уравнения);
 - корни характеристического уравнения;
- корни характеристического уравнения;
 – постоянные интегрирования;
nk – кратность к-го корня.
Пусть, для примера, в цепи 10-го порядка получились такие корни характеристического уравнения:
p1=p2=p3, р4=р5, р6, р7, р8, р9=a+jb, р10=a-jb,
тогда общий вид свободной составляющей будет
– постоянные интегрирования;
nk – кратность к-го корня.
Пусть, для примера, в цепи 10-го порядка получились такие корни характеристического уравнения:
p1=p2=p3, р4=р5, р6, р7, р8, р9=a+jb, р10=a-jb,
тогда общий вид свободной составляющей будет
 7. Для нахождения n постоянных интегрирования cоставляем систему уравнений:
7. Для нахождения n постоянных интегрирования cоставляем систему уравнений:

 (1.6)
Значения величин, стоящих в левой части этого уравнения называются зависимыми начальными условиями (ЗНУ), которые находятся с помощью независимых начальных условий (ННУ), уравнений Кирхгофа и компонентных уравнений.
ННУ- это токи в индуктивностях и напряжения на конденсаторах в момент времени непосредственно после коммутации
(1.6)
Значения величин, стоящих в левой части этого уравнения называются зависимыми начальными условиями (ЗНУ), которые находятся с помощью независимых начальных условий (ННУ), уравнений Кирхгофа и компонентных уравнений.
ННУ- это токи в индуктивностях и напряжения на конденсаторах в момент времени непосредственно после коммутации 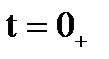 . ННУ могут быть найдены из расчета цепи до коммутации любым известным методом расчета цепей. Для ННУ выполняются законы коммутации, основанные на принципе непрерывности энергии электромагнитного поля. Из этого принципа вытекает, что невозможны скачкообразные изменения токов в индуктивностях и напряжений на емкостях.
30. Расскажите о переходных процессах и законах коммутации в электрических цепях.
В электрических цепях могут происходить события, приводящие к изменениям параметров или в топологии схемы. Такие изменения называются коммутациями. Примером коммутации могут быть:
подключение (отключение) источника;
короткое замыкание в какой-либо ветви;
резкое изменение амплитуды или фазы источника.
На схемах для обозначения коммутации используют ключевой элемент с указанием стрелочкой вида коммутации (замыкание, размыкание) и момента времени.
Ключ считается идеальным элементом. Сопротивление ключа в открытом состоянии принимается равным нулю, а закрытом – бесконечности. Время коммутации есть бесконечно малая величина, то есть переход из одного состояния в другое происходит мгновенно.
Момент коммутации является границей между, так называемыми, до коммутационным (предшествующим) и переходным процессами (ПП). Теоретически переходный процесс длится бесконечно долго, но на практике это время считают конечным в силу затухающего характера переходного процесса. Во время переходного процесса электрическая величина стремится к некоторому установившемуся значению, по достижению которого с точностью до 99%, переходный процесс считают закончившимся. Дальнейшее состояние цепи называют установившимся процессом.
. ННУ могут быть найдены из расчета цепи до коммутации любым известным методом расчета цепей. Для ННУ выполняются законы коммутации, основанные на принципе непрерывности энергии электромагнитного поля. Из этого принципа вытекает, что невозможны скачкообразные изменения токов в индуктивностях и напряжений на емкостях.
30. Расскажите о переходных процессах и законах коммутации в электрических цепях.
В электрических цепях могут происходить события, приводящие к изменениям параметров или в топологии схемы. Такие изменения называются коммутациями. Примером коммутации могут быть:
подключение (отключение) источника;
короткое замыкание в какой-либо ветви;
резкое изменение амплитуды или фазы источника.
На схемах для обозначения коммутации используют ключевой элемент с указанием стрелочкой вида коммутации (замыкание, размыкание) и момента времени.
Ключ считается идеальным элементом. Сопротивление ключа в открытом состоянии принимается равным нулю, а закрытом – бесконечности. Время коммутации есть бесконечно малая величина, то есть переход из одного состояния в другое происходит мгновенно.
Момент коммутации является границей между, так называемыми, до коммутационным (предшествующим) и переходным процессами (ПП). Теоретически переходный процесс длится бесконечно долго, но на практике это время считают конечным в силу затухающего характера переходного процесса. Во время переходного процесса электрическая величина стремится к некоторому установившемуся значению, по достижению которого с точностью до 99%, переходный процесс считают закончившимся. Дальнейшее состояние цепи называют установившимся процессом.
 Рис. 1.1
Учет переходных процессов при проектировании и эксплуатации электротехнических устройств, как правило, обязателен. Например, в момент пуска двигателя в его обмотках могут возникать пусковые токи в несколько раз превышающие номинальные токи. Возможны в цепях и коммутационные перенапряжения, способные вызвать пробой изоляции, и как следствие, короткое замыкание.
Расчет переходных процессов основывается на решении (интегрировании) дифференциального уравнения, которым искомая величина (ток, напряжение, потокосцепление, заряд) связана с независимой переменной t – временем. Это уравнение получается из системы интегро-дифференциальных уравнений, которыми можно описать цепь по законам Кирхгофа. Оно называется линейным обыкновенным неоднородным дифференциальным уравнением (ОДУ) n-го порядка с постоянными коэффициентами вида
Рис. 1.1
Учет переходных процессов при проектировании и эксплуатации электротехнических устройств, как правило, обязателен. Например, в момент пуска двигателя в его обмотках могут возникать пусковые токи в несколько раз превышающие номинальные токи. Возможны в цепях и коммутационные перенапряжения, способные вызвать пробой изоляции, и как следствие, короткое замыкание.
Расчет переходных процессов основывается на решении (интегрировании) дифференциального уравнения, которым искомая величина (ток, напряжение, потокосцепление, заряд) связана с независимой переменной t – временем. Это уравнение получается из системы интегро-дифференциальных уравнений, которыми можно описать цепь по законам Кирхгофа. Оно называется линейным обыкновенным неоднородным дифференциальным уравнением (ОДУ) n-го порядка с постоянными коэффициентами вида
 (1.1)
Для его однозначного разрешения должны быть определены n начальных условий (НУ) (1.2), которым удовлетворяют постоянные интегрирования:
(1.1)
Для его однозначного разрешения должны быть определены n начальных условий (НУ) (1.2), которым удовлетворяют постоянные интегрирования:

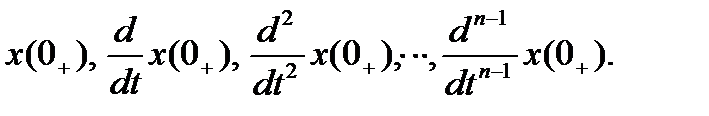 (1.2)
Из теории дифференциальных уравнений мы знаем, что решением уравнения (1.1) является сумма его частного решения для
(1.2)
Из теории дифференциальных уравнений мы знаем, что решением уравнения (1.1) является сумма его частного решения для  и общего решения однородного дифференциального уравнения вида
и общего решения однородного дифференциального уравнения вида  (1.3)
Частное решение уравнения (1.1) называют установившейся или “принуждённой” составляющей, а решение уравнения (1.3) называют свободной составляющей
(1.3)
Частное решение уравнения (1.1) называют установившейся или “принуждённой” составляющей, а решение уравнения (1.3) называют свободной составляющей
 (1.4)
Ток свободной составляющей переходного процесса обусловлен разницей энергий реактивных элементов до коммутации и в установившемся режиме. Ток принужденной составляющей обусловлен действием источников в цепи после коммутации.
I закон коммутации:
Ток через индуктивность непосредственно до коммутации iL(0–) равен току через туже индуктивность непосредственно после коммутации: iL(0–) = iL(0+).
II закон коммутации: uc(0–) = uc(0+).
В общем случае задача анализа переходных процессов заключается в определении мгновенных значений токов или напряжений всех или части ветвей электрической цепи в произвольный момент времени после коммутации и может быть сведена к решению дифференциального уравнения цепи при t>0.
36.Перечислите способы определения параметров систем уравнений четырехполюсника. Приведите примеры.
Способы определения параметров четырехполюсников
Определение параметров простейших четырехполюсников. Рассмотрим схемы простейших четырехполюсников, которые изображены на рис. 5.7,а и б.
(1.4)
Ток свободной составляющей переходного процесса обусловлен разницей энергий реактивных элементов до коммутации и в установившемся режиме. Ток принужденной составляющей обусловлен действием источников в цепи после коммутации.
I закон коммутации:
Ток через индуктивность непосредственно до коммутации iL(0–) равен току через туже индуктивность непосредственно после коммутации: iL(0–) = iL(0+).
II закон коммутации: uc(0–) = uc(0+).
В общем случае задача анализа переходных процессов заключается в определении мгновенных значений токов или напряжений всех или части ветвей электрической цепи в произвольный момент времени после коммутации и может быть сведена к решению дифференциального уравнения цепи при t>0.
36.Перечислите способы определения параметров систем уравнений четырехполюсника. Приведите примеры.
Способы определения параметров четырехполюсников
Определение параметров простейших четырехполюсников. Рассмотрим схемы простейших четырехполюсников, которые изображены на рис. 5.7,а и б.
 Рис. 5.7. Схемы простейших четырехполюсников.
На основании закона Кирхгофа для схемы (рис. 5.7,а) можно записать: U1= U2 + I2Z1; I1 = I2. На основании сравнения этих уравнений с уравнениями передачи в А-параметрах (5.7) для рассматриваемой схемы можно записать матрицу А-параметров:
Рис. 5.7. Схемы простейших четырехполюсников.
На основании закона Кирхгофа для схемы (рис. 5.7,а) можно записать: U1= U2 + I2Z1; I1 = I2. На основании сравнения этих уравнений с уравнениями передачи в А-параметрах (5.7) для рассматриваемой схемы можно записать матрицу А-параметров:
 (5.71)
Для схемы рис. 5.7,б на основании закона Кирхгофа запишем следующие уравнения: U1 = U2; I1 = U2/Z2 + I2 и поэтому матрица А-параметров будет иметь вид:
(5.71)
Для схемы рис. 5.7,б на основании закона Кирхгофа запишем следующие уравнения: U1 = U2; I1 = U2/Z2 + I2 и поэтому матрица А-параметров будет иметь вид:
 (5.72)
Зная матрицы А-параметров, используя таблицу пересчета (5.1), можно получить матрицы Y, Z и Н-параметров.
Используя схемы простейших четырехполюсников можно составить схемы типовых четырехполюсников.
Определение параметров типовых четырехполюсников. К типовым пассивным четырехполюсникам относятся Г-, Т-, П-образные схемы, которые изображены на рис. 5.8,а, б, в.
(5.72)
Зная матрицы А-параметров, используя таблицу пересчета (5.1), можно получить матрицы Y, Z и Н-параметров.
Используя схемы простейших четырехполюсников можно составить схемы типовых четырехполюсников.
Определение параметров типовых четырехполюсников. К типовым пассивным четырехполюсникам относятся Г-, Т-, П-образные схемы, которые изображены на рис. 5.8,а, б, в.
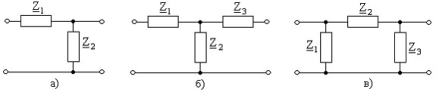 Рис. 5.8 Схемы Г-образного (а), Т-образного (б) и П-образного (в) четырехполюсников.
Г-образный четырехполюсник (рис. 5.8,а) получается путем каскадного соединения простейших четырехполюсников (рис. 5.7,а и б). Следовательно, его матрицу А-параметров можно получить перемножением матриц (5.71) и (5.72):
Рис. 5.8 Схемы Г-образного (а), Т-образного (б) и П-образного (в) четырехполюсников.
Г-образный четырехполюсник (рис. 5.8,а) получается путем каскадного соединения простейших четырехполюсников (рис. 5.7,а и б). Следовательно, его матрицу А-параметров можно получить перемножением матриц (5.71) и (5.72):
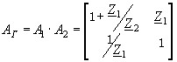 (5.73)
Т-образный четырехполюсник (рис. 5.8,б) образуется путем каскадного соединения Г- образной схемы (рис. 5.8,а) с элементами Z1 и Z2 и схемы (рис. 5.7,а) с элементом Z3 в продольном плече. Тогда его матрица А-параметров определяется как произведение матриц Аг и матрицы (5.71), в которой Z1 заменено Z3.
(5.73)
Т-образный четырехполюсник (рис. 5.8,б) образуется путем каскадного соединения Г- образной схемы (рис. 5.8,а) с элементами Z1 и Z2 и схемы (рис. 5.7,а) с элементом Z3 в продольном плече. Тогда его матрица А-параметров определяется как произведение матриц Аг и матрицы (5.71), в которой Z1 заменено Z3.
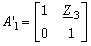 Выполняя перемножение матриц Аг и А′1 получим:
Выполняя перемножение матриц Аг и А′1 получим:
 (5.74)
П-образный четырехполюсник (рис. 5.8,в) образуется путем каскадного соединения простейшего четырехполюсника (рис. 5.7,б) с элементомZ1 и Г-образного четырехполюсника (рис. 5.8,а) с элементами Z2 и Z3 в продольном и в поперечном плечах. Следовательно, его матрицу А-параметров можно получить перемножением матриц соединенных четырехполюсников, т.е.:
(5.74)
П-образный четырехполюсник (рис. 5.8,в) образуется путем каскадного соединения простейшего четырехполюсника (рис. 5.7,б) с элементомZ1 и Г-образного четырехполюсника (рис. 5.8,а) с элементами Z2 и Z3 в продольном и в поперечном плечах. Следовательно, его матрицу А-параметров можно получить перемножением матриц соединенных четырехполюсников, т.е.:
 (5.75)
Матрица А′г получена из (5.73) путем замены Z1 на Z2 и Z2 на Z3, а матрица А′2 – из (5.72) путем замены Z2 на Z1.
Зная А-параметры типовых четырехполюсников используя таблицу (5.1) можно определить другие интересующие нас параметры Г-, Т- и П-образных четырехполюсников.
При анализе сложных четырехполюсников необходимо выделить в их составе простейшие и типовые четырехполюсники и установить способы их соединения. После этого с помощью матричных методов расчета можно определить матрицы сложного четырехполюсника.
Экспериментальный способ определения параметров четырехполюсника. Если схема четырехполюсника неизвестна, то его параметры можно определить экспериментальным путем, используя режимы холостого хода и короткого замыкания.
(5.75)
Матрица А′г получена из (5.73) путем замены Z1 на Z2 и Z2 на Z3, а матрица А′2 – из (5.72) путем замены Z2 на Z1.
Зная А-параметры типовых четырехполюсников используя таблицу (5.1) можно определить другие интересующие нас параметры Г-, Т- и П-образных четырехполюсников.
При анализе сложных четырехполюсников необходимо выделить в их составе простейшие и типовые четырехполюсники и установить способы их соединения. После этого с помощью матричных методов расчета можно определить матрицы сложного четырехполюсника.
Экспериментальный способ определения параметров четырехполюсника. Если схема четырехполюсника неизвестна, то его параметры можно определить экспериментальным путем, используя режимы холостого хода и короткого замыкания.
 Рис. 5.9. Схема для экспериментального определения параметров четырехполюсника.
Определим А-параметры четырехполюсника.
Для этого на входе четырехполюсника подключим вольтметр (V), амперметр (А) и фазометр (φ), как показано на рис. 5.9.
Переведем четырехполюсник в режим холостого хода по выходу (I2=0) и измерим с помощью приборов Iх.х.1, Uх.х.1 и φх.х.1.
В случае, когда I2 = 0 система А-параметров имеет вид:
Рис. 5.9. Схема для экспериментального определения параметров четырехполюсника.
Определим А-параметры четырехполюсника.
Для этого на входе четырехполюсника подключим вольтметр (V), амперметр (А) и фазометр (φ), как показано на рис. 5.9.
Переведем четырехполюсник в режим холостого хода по выходу (I2=0) и измерим с помощью приборов Iх.х.1, Uх.х.1 и φх.х.1.
В случае, когда I2 = 0 система А-параметров имеет вид:
 (5.76)
Из (5.76) получим
(5.76)
Из (5.76) получим
 (5.77)
Переведем четырехполюсник в режим короткого замыкания по выходу (U2 = 0). Измерим Iк.з.1, Uк.з.1 и φк.з.1, тогда система А-параметров будет иметь вид:
(5.77)
Переведем четырехполюсник в режим короткого замыкания по выходу (U2 = 0). Измерим Iк.з.1, Uк.з.1 и φк.з.1, тогда система А-параметров будет иметь вид:
 (5.78)
Из (5.78) получим
(5.78)
Из (5.78) получим
 (5.79)
Подключим приборы к зажимам (2-2) и переведем четырехполюсник в режим холостого хода по входу (I1 = 0) и измерим Iх.х.2, Uх.х.2 и φх.х.2. Тогда имеем:
(5.79)
Подключим приборы к зажимам (2-2) и переведем четырехполюсник в режим холостого хода по входу (I1 = 0) и измерим Iх.х.2, Uх.х.2 и φх.х.2. Тогда имеем:
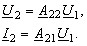 (5.80)
Из (5.80) получим
(5.80)
Из (5.80) получим
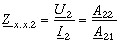 (5.81)
Четвертое уравнение получим, используя соотношение:
(5.81)
Четвертое уравнение получим, используя соотношение:
 (5.82)
Решив систему уравнений (5.77), (5.79), (5.81) и (5.82), найдем А-параметры:
(5.82)
Решив систему уравнений (5.77), (5.79), (5.81) и (5.82), найдем А-параметры:


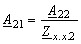

 Рис. 6.7. Схема пассивного RC-фильтра нижних частот (а) и его АЧХ (б).
С увеличением частоты сопротивление конденсатора уменьшается, что приводит к уменьшению коэффициента передачи (рис. 6.7,б).
В RC-фильтре верхних частот (ФВЧ) конденсатор включён в продольное плечо (рис. 6.8,а). Поэтому на низких частотах его сопротивление значительно больше сопротивление резистора параллельного плеча и коэффициент передачи мал. С увеличением частоты сопротивление конденсатора уменьшается, что приводит к увеличению коэффициента передачи (рис. 6.8,б).
Рис. 6.7. Схема пассивного RC-фильтра нижних частот (а) и его АЧХ (б).
С увеличением частоты сопротивление конденсатора уменьшается, что приводит к уменьшению коэффициента передачи (рис. 6.7,б).
В RC-фильтре верхних частот (ФВЧ) конденсатор включён в продольное плечо (рис. 6.8,а). Поэтому на низких частотах его сопротивление значительно больше сопротивление резистора параллельного плеча и коэффициент передачи мал. С увеличением частоты сопротивление конденсатора уменьшается, что приводит к увеличению коэффициента передачи (рис. 6.8,б).
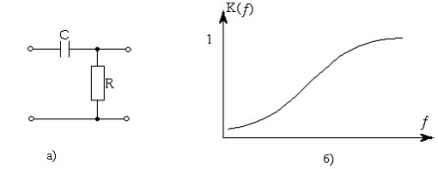 Рис. 6.8. Схема пассивного RC-фильтра верхних частот (а) и его АЧХ (б).
Рассмотренные ФНЧ и ФВЧ, состоящие из нескольких однотипных звеньев RC, называются цепочечными RC-фильтрами.
В качестве полосового RC-фильтра на низких частотах применяется Г-образный RC-фильтр (рис. 6.9,а).
Рис. 6.8. Схема пассивного RC-фильтра верхних частот (а) и его АЧХ (б).
Рассмотренные ФНЧ и ФВЧ, состоящие из нескольких однотипных звеньев RC, называются цепочечными RC-фильтрами.
В качестве полосового RC-фильтра на низких частотах применяется Г-образный RC-фильтр (рис. 6.9,а).
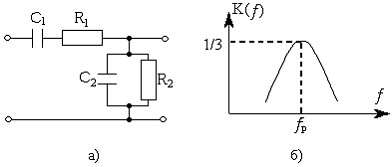 Рис. 6.9. Схема пассивного полосового RC-фильтра (а) и его АЧХ (б).
31. Как определить согласованное сопротивление и постоянную передачи симметричного четырехполюсника через сопротивление холостого хода и короткого замыкания.
Для этого достаточно произвести измерения при холостом ходе, когда Zпр=∞ и I2=0, Zпр — сопротивление приемника и при коротком замыкании, когда Zпр=0 и U2=0. При этих опытах подводимая мощность идет только на покрытие потерь четырехполюсника, тогда, как при номинальном режиме она значительно больше. Один из наиболее удобных экспериментальных методов определения коэффициентов четырехполюсника основан на опытах холостого хода и короткого замыкания при питании со стороны вторичных зажимов и опыте холостого хода при питании со стороны первичных зажимов. В этом случае при
Рис. 6.9. Схема пассивного полосового RC-фильтра (а) и его АЧХ (б).
31. Как определить согласованное сопротивление и постоянную передачи симметричного четырехполюсника через сопротивление холостого хода и короткого замыкания.
Для этого достаточно произвести измерения при холостом ходе, когда Zпр=∞ и I2=0, Zпр — сопротивление приемника и при коротком замыкании, когда Zпр=0 и U2=0. При этих опытах подводимая мощность идет только на покрытие потерь четырехполюсника, тогда, как при номинальном режиме она значительно больше. Один из наиболее удобных экспериментальных методов определения коэффициентов четырехполюсника основан на опытах холостого хода и короткого замыкания при питании со стороны вторичных зажимов и опыте холостого хода при питании со стороны первичных зажимов. В этом случае при  на основании уравнений
на основании уравнений 
 получаем
получаем  (1)
При
(1)
При 
 (2)и при
(2)и при 
 (3) для симметричного ЧП измерения сопротивления короткого замыкания и проводимости холостого хода со стороны первичных зажимов достаточно, т.к. существуют связи AD-BC=1 A=D.
Zk=U1k/I1k=B/D Y1x=I1x/U1x=C/A Для оценки собственных потерь энергии в четырехполюснике вводят в качестве меры, характеризующей, как передает четырехполюсник энергию (с потерями или без), понятие характеристическая (собственная) постоянная передачи четырехполюсника. В качестве такой характеристики используют логарифмическое отношение мощностей на входе S1 = U1I1 и выходе S2 = U2I2 четырехполюсника, которое записывается в виде следующего выражения:
(3) для симметричного ЧП измерения сопротивления короткого замыкания и проводимости холостого хода со стороны первичных зажимов достаточно, т.к. существуют связи AD-BC=1 A=D.
Zk=U1k/I1k=B/D Y1x=I1x/U1x=C/A Для оценки собственных потерь энергии в четырехполюснике вводят в качестве меры, характеризующей, как передает четырехполюсник энергию (с потерями или без), понятие характеристическая (собственная) постоянная передачи четырехполюсника. В качестве такой характеристики используют логарифмическое отношение мощностей на входе S1 = U1I1 и выходе S2 = U2I2 четырехполюсника, которое записывается в виде следующего выражения:  Для симметричного четырехполюсника Zс1 = Zс2 = Zс, тогда из
Для симметричного четырехполюсника Zс1 = Zс2 = Zс, тогда из  следует:
следует: 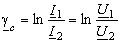 34. Расскажите о корнях характеристического уравнения и типе переходного процесса в последовательной RLC цепи.
Рассмотрим процессы установления при включении источника постоянного напряжения на вход последовательной RLC- цепи (рис. 1.24).
34. Расскажите о корнях характеристического уравнения и типе переходного процесса в последовательной RLC цепи.
Рассмотрим процессы установления при включении источника постоянного напряжения на вход последовательной RLC- цепи (рис. 1.24).
 рис. 1.24
В данном случае электрическая цепь после коммутации содержит два реактивных элемента - индуктивность и емкость. Это означает, что дифференциальное уравнение цепи должно иметь второй порядок и поэтому должны быть определены два независимых начальных условия. Очевидно, что до коммутации цепь находилась в состоянии покоя, что соответствует нулевым начальным условиям: uC(0+) = uC(0-) = 0; i(0+) = i(0-) = 0.
Согласно второму закону Кирхгофа для цепи после коммутации справедливо следующее уравнение:
uR(t) + uL(t) + uC(t) = U0; (1.24)
Будем интересоваться напряжением на емкости uC(t) и поэтому другие напряжения, входящие в (1.24), а именно, напряжение на резисторе uR(t) и напряжение на индуктивности uL(t) выразим через uC(t):
рис. 1.24
В данном случае электрическая цепь после коммутации содержит два реактивных элемента - индуктивность и емкость. Это означает, что дифференциальное уравнение цепи должно иметь второй порядок и поэтому должны быть определены два независимых начальных условия. Очевидно, что до коммутации цепь находилась в состоянии покоя, что соответствует нулевым начальным условиям: uC(0+) = uC(0-) = 0; i(0+) = i(0-) = 0.
Согласно второму закону Кирхгофа для цепи после коммутации справедливо следующее уравнение:
uR(t) + uL(t) + uC(t) = U0; (1.24)
Будем интересоваться напряжением на емкости uC(t) и поэтому другие напряжения, входящие в (1.24), а именно, напряжение на резисторе uR(t) и напряжение на индуктивности uL(t) выразим через uC(t):
 (1.25)
После подстановки (1.25) в (1.24) получим дифференциальное уравнение:
(1.25)
После подстановки (1.25) в (1.24) получим дифференциальное уравнение:
 (1.26)
Полученное уравнение является линейным дифференциальным неоднородным уравнением второго порядка с постоянными коэффициентами. Его решение будем искать в виде: uC(t) = uCсв(t) + uCвын.
Для определения свободной составляющей записываем соответствующее характеристическое уравнение LCp2 + Rcp + 1 = 0 и определяем его корни:
(1.26)
Полученное уравнение является линейным дифференциальным неоднородным уравнением второго порядка с постоянными коэффициентами. Его решение будем искать в виде: uC(t) = uCсв(t) + uCвын.
Для определения свободной составляющей записываем соответствующее характеристическое уравнение LCp2 + Rcp + 1 = 0 и определяем его корни:
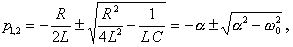 (1.27)
где введены следующие обозначения: a = R / 2L - коэффициент затухания; w 0 = 1/ Ö LC - резонансная частота контура. Далее записываем выражение для свободной составляющей
(1.27)
где введены следующие обозначения: a = R / 2L - коэффициент затухания; w 0 = 1/ Ö LC - резонансная частота контура. Далее записываем выражение для свободной составляющей
 Вынужденную составляющую решения определим как установившееся значение напряжения на емкости в режиме постоянного тока в цепи после коммутации (рис. 1.25).
Вынужденную составляющую решения определим как установившееся значение напряжения на емкости в режиме постоянного тока в цепи после коммутации (рис. 1.25).
 Рис. 1.25.
Из уравнения по второму закону Кирхгофа получим uCуст = uCвын = U0. Таким образом, полное решение для напряжения
Рис. 1.25.
Из уравнения по второму закону Кирхгофа получим uCуст = uCвын = U0. Таким образом, полное решение для напряжения
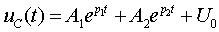 (1.28)
и для тока
(1.28)
и для тока
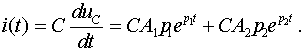 (1.29)
Выражение для тока необходимо для определения постоянных интегрирования. Используя нулевые начальные условия, из (1.28) и (1.29) при t = 0 получим: uC(0+)= A1 + A2 + U0 = 0; i(0+) = CA1p1 + CA2p2 = 0. Решение этой системы уравнений дает выражения для постоянных интегрирования:
(1.29)
Выражение для тока необходимо для определения постоянных интегрирования. Используя нулевые начальные условия, из (1.28) и (1.29) при t = 0 получим: uC(0+)= A1 + A2 + U0 = 0; i(0+) = CA1p1 + CA2p2 = 0. Решение этой системы уравнений дает выражения для постоянных интегрирования:
 (1.30)
Дальнейшая конкретизация решения связана с видом корней р1 и р2 характеристического уравнения. В зависимости от соотношения между параметрами цепи возможны следующие виды корней (1.27):
a > w 0 - корни вещественные, отрицательные, неравные, что соответствует, как будет показано ниже, апериодическому режиму переходных процессов;
a = w 0 - корни вещественные отрицательные, равные. Режим называется критическим.
a < w 0 - корни комплексные сопряженные с отрицательной вещественной частью, что соответствует колебательному режиму;
32. Расскажите о постоянных времени RL и RC последовательных цепочек и их экспериментальном определении.
Переходные процессы. Переходным называется процесс изменения электрических величин в цепи при ее переходе из одного установившегося режима в другой. При анализе переходных процессов ток, напряжение или заряд в некоторой точке цепи обычно представляют в виде функции времени. Рассмотрим цепь с источником напряжения (батареей с ЭДС Eg), представленную на рис. 6. После замыкания ключа сумма мгновенных значений напряжения на резисторе и конденсаторе должна быть равна Eg:
(1.30)
Дальнейшая конкретизация решения связана с видом корней р1 и р2 характеристического уравнения. В зависимости от соотношения между параметрами цепи возможны следующие виды корней (1.27):
a > w 0 - корни вещественные, отрицательные, неравные, что соответствует, как будет показано ниже, апериодическому режиму переходных процессов;
a = w 0 - корни вещественные отрицательные, равные. Режим называется критическим.
a < w 0 - корни комплексные сопряженные с отрицательной вещественной частью, что соответствует колебательному режиму;
32. Расскажите о постоянных времени RL и RC последовательных цепочек и их экспериментальном определении.
Переходные процессы. Переходным называется процесс изменения электрических величин в цепи при ее переходе из одного установившегося режима в другой. При анализе переходных процессов ток, напряжение или заряд в некоторой точке цепи обычно представляют в виде функции времени. Рассмотрим цепь с источником напряжения (батареей с ЭДС Eg), представленную на рис. 6. После замыкания ключа сумма мгновенных значений напряжения на резисторе и конденсаторе должна быть равна Eg:
 или, иначе,
или, иначе,

 Рис. 6. ПЕРЕХОДНЫЙ ПРОЦЕСС начинается при замыкании ключа (Eg - постоянная ЭДС батареи).
Поскольку i = dq/dt, уравнение (10) можно переписать в виде дифференциального уравнения
Рис. 6. ПЕРЕХОДНЫЙ ПРОЦЕСС начинается при замыкании ключа (Eg - постоянная ЭДС батареи).
Поскольку i = dq/dt, уравнение (10) можно переписать в виде дифференциального уравнения
 решение которого таково:
решение которого таково:
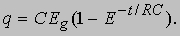 Соответствующий ток равен:
Соответствующий ток равен:
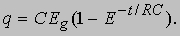 где e - основание натуральных логарифмов. На рис. 7 представлены графики изменения заряда конденсатора q и тока i во времени. В начальный момент (t = 0), когда ключ только замкнут, заряд конденсатора равен нулю, а ток равен Eg /R, как если бы конденсатора в цепи не было. Затем заряд конденсатора нарастает по экспоненте. Обусловленное зарядом напряжение на конденсаторе направлено навстречу ЭДС источника, и ток по экспоненте убывает до нуля. В момент замыкания ключа конденсатор эквивалентен короткому замыканию, а по истечении достаточно длительного времени (при t = беск.) - разрыву цепи.
где e - основание натуральных логарифмов. На рис. 7 представлены графики изменения заряда конденсатора q и тока i во времени. В начальный момент (t = 0), когда ключ только замкнут, заряд конденсатора равен нулю, а ток равен Eg /R, как если бы конденсатора в цепи не было. Затем заряд конденсатора нарастает по экспоненте. Обусловленное зарядом напряжение на конденсаторе направлено навстречу ЭДС источника, и ток по экспоненте убывает до нуля. В момент замыкания ключа конденсатор эквивалентен короткому замыканию, а по истечении достаточно длительного времени (при t = беск.) - разрыву цепи.
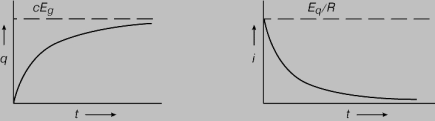 Рис. 7. ПЕРЕХОДНЫЙ ПРОЦЕСС, зависимость заряда конденсатора q и тока через конденсатор i от времени t.
Постоянная времени RC-цепи определяется как время, за которое заряд достигает значения, на 1/e (36,8%) отличающегося от конечного значения. Она дается выражением
Рис. 7. ПЕРЕХОДНЫЙ ПРОЦЕСС, зависимость заряда конденсатора q и тока через конденсатор i от времени t.
Постоянная времени RC-цепи определяется как время, за которое заряд достигает значения, на 1/e (36,8%) отличающегося от конечного значения. Она дается выражением
 Аналогичные рассуждения можно провести для RL-цепи, представленной на рис. 8. Сумма мгновенных напряжений eR и eL должна быть равна Eg. Это условие записывается в виде дифференциального уравнения
Аналогичные рассуждения можно провести для RL-цепи, представленной на рис. 8. Сумма мгновенных напряжений eR и eL должна быть равна Eg. Это условие записывается в виде дифференциального уравнения
 решение которого таково:
решение которого таково:
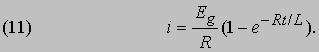
 Рис. 8. RL-ЦЕПЬ. Сумма мгновенных значений напряжений eR и eL должна быть равна Eg.
Рис. 8. RL-ЦЕПЬ. Сумма мгновенных значений напряжений eR и eL должна быть равна Eg.
 Составим уравнения по методу контурных токов
Составим уравнения по методу контурных токов
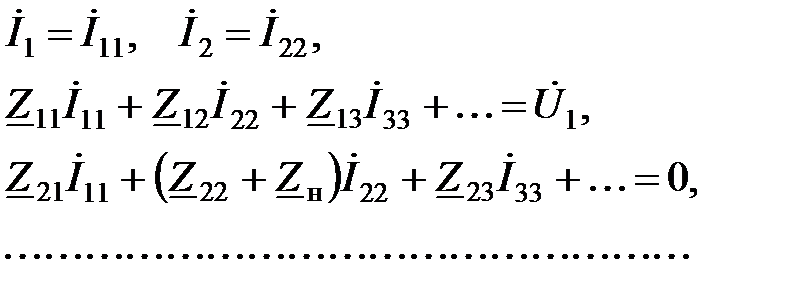 Поскольку
Поскольку  , то, перенеся величину
, то, перенеся величину  в правую часть второго уравнения, приведем систему уравнений к виду
в правую часть второго уравнения, приведем систему уравнений к виду  (3.2)
Учитывая, что правые части всех уравнений, кроме первых двух, равны нулю, получим на основании принципа наложения следующее решение
(3.2)
Учитывая, что правые части всех уравнений, кроме первых двух, равны нулю, получим на основании принципа наложения следующее решение
 (3.3) Коэффициенты в (3.3) имеют размерность проводимости, введем соответствующие обозначения
(3.3) Коэффициенты в (3.3) имеют размерность проводимости, введем соответствующие обозначения 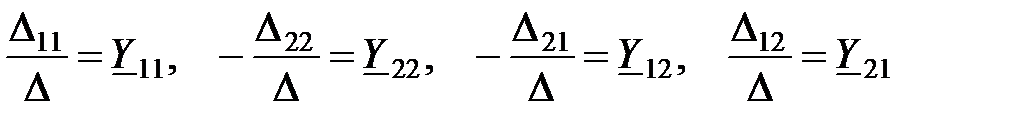 Тогда уравнения четырехполюсника, записанные в Y-форме, связывающие токи с напряжениями, имеют вид
Тогда уравнения четырехполюсника, записанные в Y-форме, связывающие токи с напряжениями, имеют вид  (3.4) Полученные соотношения в матричной форме имеют вид:
(3.4) Полученные соотношения в матричной форме имеют вид: 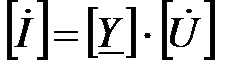 . Для линейной пассивной цепи
. Для линейной пассивной цепи  , а следовательно,
, а следовательно,  . Из четырех Y- параметров независимых три, т.к.
. Из четырех Y- параметров независимых три, т.к.  Решив (3.4) относительно напряжений
Решив (3.4) относительно напряжений  и
и  , получим уравнения четырехполюсника, записанные в Z-форме, связывающие напряжения и токи
, получим уравнения четырехполюсника, записанные в Z-форме, связывающие напряжения и токи  (3.5) где
(3.5) где  (3,6) при этом
(3,6) при этом 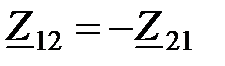 .Из четырех Z –параметров независимых три. Уравнение (3.5) в матричной форме:
.Из четырех Z –параметров независимых три. Уравнение (3.5) в матричной форме:  . Наиболее распространенной формой записи уравнений четырехполюсника является такая, при которой входные ток и напряжение выражаются через выходные напряжение и ток. Из уравнений (3.3) можно записать
. Наиболее распространенной формой записи уравнений четырехполюсника является такая, при которой входные ток и напряжение выражаются через выходные напряжение и ток. Из уравнений (3.3) можно записать
 .(3.7) Подставим (3.7) в
первое уравнение (3.3)
.(3.7) Подставим (3.7) в
первое уравнение (3.3)  (3.8) Введем обозначения
(3.8) Введем обозначения  – величина безразмерная;
– величина безразмерная;  – величина, измеряемая в омах;
– величина, измеряемая в омах;  – величина, измеряемая в сименсах;
– величина, измеряемая в сименсах;  – величина безразмерная. При этом будут справедливы соотношения
– величина безразмерная. При этом будут справедливы соотношения
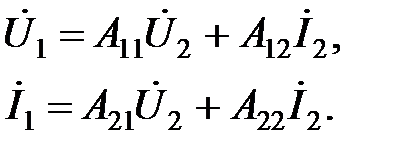 (3.9) В матричной форме эти уравнения имеют вид
(3.9) В матричной форме эти уравнения имеют вид  Уравнения (3.9) называют уравнения четырехполюсника в А-параметрах. Учитывая, что
Уравнения (3.9) называют уравнения четырехполюсника в А-параметрах. Учитывая, что  , можно показать, что определитель матрицы А равен единице:
, можно показать, что определитель матрицы А равен единице:  (3.10)Из этого соотношения следует, что для определения
(3.10)Из этого соотношения следует, что для определения  и
и  достаточно знать только три коэффициента из четырех, т.е. среди А –параметров только три независимые, аналогично для Z–, Y– форм. Таким образом, зная, что Y, Z, A – параметры зависят от параметров элементов и конфигурации схемы четырехполюсника, можно сформулировать связь вход–выход, не прибегая к расчету токов и напряжений во внутренней части четырехполюсника, которая может представлять собой весьма сложную электрическую цепь
35.Расскажите о способах соединения двух четырехполюсников и рациональных формах определения коэффициентов систем уравнений, описывающих эквивалентный четырехполюсник.
При последовательном соединении двух удобно пользоваться матрицами Z. Для этого вида соединения
достаточно знать только три коэффициента из четырех, т.е. среди А –параметров только три независимые, аналогично для Z–, Y– форм. Таким образом, зная, что Y, Z, A – параметры зависят от параметров элементов и конфигурации схемы четырехполюсника, можно сформулировать связь вход–выход, не прибегая к расчету токов и напряжений во внутренней части четырехполюсника, которая может представлять собой весьма сложную электрическую цепь
35.Расскажите о способах соединения двух четырехполюсников и рациональных формах определения коэффициентов систем уравнений, описывающих эквивалентный четырехполюсник.
При последовательном соединении двух удобно пользоваться матрицами Z. Для этого вида соединения  т. е. напряжения на выходах и входах отдельных четырехполюсников в результирующем четырехполюснике складываются. Записывая уравнения передачи в Z-форме для каждого четырехполюсника
т. е. напряжения на выходах и входах отдельных четырехполюсников в результирующем четырехполюснике складываются. Записывая уравнения передачи в Z-форме для каждого четырехполюсника  При последовательном соединении четырехполюсников матрица Z результирующего четырехполюсника равна сумме одноименных матриц соединенных четырехполюсников: Z = Z' + Z".
Совершенно аналогично доказывается, что при параллельном соединении четырехполюсников (рис. 12.6), где
При последовательном соединении четырехполюсников матрица Z результирующего четырехполюсника равна сумме одноименных матриц соединенных четырехполюсников: Z = Z' + Z".
Совершенно аналогично доказывается, что при параллельном соединении четырехполюсников (рис. 12.6), где 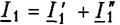 и
и 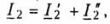 матрица Y результирующего четырехполюсника равна сумме одноименных матриц соединяемых четырехполюсников: Y = Y' + Y".
Матрицы F удобно применять при смешанном — последовательно-параллельном соединении четырехполюсников (рис. 12.7, а). При этом Н = Н' + Н".
Матрицы F удобно применять при параллельно-последовательном соединении четырехполюсников (рис. 12.7, б). При этом F = F' + F"
Способы соединения четырехполюсников
Каскадное соединение четырехполюсников. Каскадным соединением четырехполюсников называется такое соединение, при котором выход предыдущего четырехполюсника соединяется со входом последующего.
матрица Y результирующего четырехполюсника равна сумме одноименных матриц соединяемых четырехполюсников: Y = Y' + Y".
Матрицы F удобно применять при смешанном — последовательно-параллельном соединении четырехполюсников (рис. 12.7, а). При этом Н = Н' + Н".
Матрицы F удобно применять при параллельно-последовательном соединении четырехполюсников (рис. 12.7, б). При этом F = F' + F"
Способы соединения четырехполюсников
Каскадное соединение четырехполюсников. Каскадным соединением четырехполюсников называется такое соединение, при котором выход предыдущего четырехполюсника соединяется со входом последующего.
 Рис. 5.3. Схема каскадного соединения двух четырехполюсников.
На рис. 5.3 показано каскадное соединение двух четырехполюсников, которые заданы своими матрицами А-параметров:
Рис. 5.3. Схема каскадного соединения двух четырехполюсников.
На рис. 5.3 показано каскадное соединение двух четырехполюсников, которые заданы своими матрицами А-параметров:
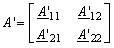
 (5.59)
Зная матрицы двух четырехполюсников (5.59) запишем их уравнения передачи в А-параметрах в матричном виде, используя обозначения, приведенные на рис. 5.3:
(5.59)
Зная матрицы двух четырехполюсников (5.59) запишем их уравнения передачи в А-параметрах в матричном виде, используя обозначения, приведенные на рис. 5.3:
 (5.60)
(5.60)
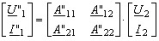 (5.61)
Из схемы рис. 5.3 видно, что
(5.61)
Из схемы рис. 5.3 видно, что
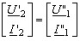 поэтому выражение (5.60) можно записать в следующем виде:
поэтому выражение (5.60) можно записать в следующем виде:
 (5.62)
Из выражения (5.62) видно, что при каскадном соединении четырехполюсников матрица А-параметров результирующего четырехполюсника равна произведению одноименных матриц соединенных четырехполюсников, т.е.:
(5.62)
Из выражения (5.62) видно, что при каскадном соединении четырехполюсников матрица А-параметров результирующего четырехполюсника равна произведению одноименных матриц соединенных четырехполюсников, т.е.:
 (5.63)
Последовательное соединение четырехполюсников. Последовательное соединение двух четырехполюсников, заданных матрицами Z-параметров, показано на рис.5.4.
(5.63)
Последовательное соединение четырехполюсников. Последовательное соединение двух четырехполюсников, заданных матрицами Z-параметров, показано на рис.5.4.
 Рис. 5.4 Схема последовательного соединения четырехполюсников.
Из рис. 5.4 видно, что
Рис. 5.4 Схема последовательного соединения четырехполюсников.
Из рис. 5.4 видно, что  и
и  .
Уравнения передачи четырехполюсников Z ′ и Z ″ в матричном виде имеют вид:
.
Уравнения передачи четырехполюсников Z ′ и Z ″ в матричном виде имеют вид:
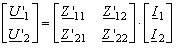 (5.64)
(5.64)
 (5.65)
Складывая матричные уравнения (5.64) и (5.65) получим:
(5.65)
Складывая матричные уравнения (5.64) и (5.65) получим:
 (5.66)
Из выражения (5.66) видно, что при последовательном соединении четырехполюсников матрица Z-параметров результирующего четырехполюсника равна сумме одноименных матриц соединенных четырехполюсников, т.е.:
(5.66)
Из выражения (5.66) видно, что при последовательном соединении четырехполюсников матрица Z-параметров результирующего четырехполюсника равна сумме одноименных матриц соединенных четырехполюсников, т.е.:
 (5.67)
Параллельное соединение четырехполюсников. Параллельное соединение четырехполюсников заданных матрицами Y- параметров показано на рис. 5.5.
(5.67)
Параллельное соединение четырехполюсников. Параллельное соединение четырехполюсников заданных матрицами Y- параметров показано на рис. 5.5.
 Рис. 5.5 Схема параллельного включения двух четырехполюсников.
Из схемы видно, что:
Рис. 5.5 Схема параллельного включения двух четырехполюсников.
Из схемы видно, что:
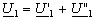


 Записывая уравнения передачи в Y-параметрах в матричном виде для каждого четырехполюсника и суммируя матричные уравнения, доказывается, что Y-матрица результирующего четырехполюсника равна сумме одноименных матриц соединенных четырехполюсников, т.е.:
Записывая уравнения передачи в Y-параметрах в матричном виде для каждого четырехполюсника и суммируя матричные уравнения, доказывается, что Y-матрица результирующего четырехполюсника равна сумме одноименных матриц соединенных четырехполюсников, т.е.:
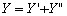 (5.69)
Смешанное соединение четырехполюсников. Схема смешанного соединения двух четырехполюсников, заданных матрицами Н-параметров приведена на рис. 5.6.
(5.69)
Смешанное соединение четырехполюсников. Схема смешанного соединения двух четырехполюсников, заданных матрицами Н-параметров приведена на рис. 5.6.
 Рис.5.6. Схема смешанного соединения двух четырехполюсников.
Записав уравнения передачи в Н-параметрах для каждого четырехполюсника в матричном виде и складывая полученные матричные равенства можно доказать, что при смешанном соединении четырехполюсников матрица Н-параметров общего четырехполюсника получается путем суммирования одноименных матриц соединяемых четырехполюсников, т.е.:
Рис.5.6. Схема смешанного соединения двух четырехполюсников.
Записав уравнения передачи в Н-параметрах для каждого четырехполюсника в матричном виде и складывая полученные матричные равенства можно доказать, что при смешанном соединении четырехполюсников матрица Н-параметров общего четырехполюсника получается путем суммирования одноименных матриц соединяемых четырехполюсников, т.е.:
 (5.70)
(5.70)


