 |
Билет 7 Теорема Лейбница для числовых рядов
|
|
|
|
Билет 5,9. Радикальный признак Коши для числового ряда
Радикальный признак Коши: Рассмотрим положительный числовой ряд  . Если существует предел:
. Если существует предел:  , то:
, то:
а) При  ряд сходится. В частности, ряд сходится при
ряд сходится. В частности, ряд сходится при  .
.
б) При  ряд расходится. В частности, ряд расходится при
ряд расходится. В частности, ряд расходится при  .
.
в) При  признак не дает ответа. Нужно использовать другой признак. Интересно отметить, что если признак Коши не даёт нам ответа на вопрос о сходимости ряда, то признак Даламбера нам тоже не даст ответа. Но если признак Даламбера не даёт ответа, то признак Коши вполне может «сработать». То есть, признак Коши является в этом смысле более сильным признаком.
признак не дает ответа. Нужно использовать другой признак. Интересно отметить, что если признак Коши не даёт нам ответа на вопрос о сходимости ряда, то признак Даламбера нам тоже не даст ответа. Но если признак Даламбера не даёт ответа, то признак Коши вполне может «сработать». То есть, признак Коши является в этом смысле более сильным признаком.
Когда нужно использовать радикальный признак Коши? Радикальный признак Коши обычно использует в тех случаях, когда общий член ряда ПОЛНОСТЬЮ находится в степени, зависящей от «эн». Либо когда корень  «хорошо» извлекается из общего члена ряда. Есть еще экзотические случаи, но ими голову забивать не будем.
«хорошо» извлекается из общего члена ряда. Есть еще экзотические случаи, но ими голову забивать не будем.
Исследовать ряд на сходимость 
Мы видим, что общий член ряда полностью находится под степенью, зависящей от  , а значит, нужно использовать радикальный признак Коши:
, а значит, нужно использовать радикальный признак Коши:

Таким образом, исследуемый ряд расходится.
(1) Оформляем общий член ряда под корень.
(2) Переписываем то же самое, только уже без корня, используя свойство степеней  .
.
(3) В показателе почленно делим числитель на знаменатель, указывая, что 
(4) В результате у нас получилась неопределенность  . Здесь можно было пойти длинным путем: возвести
. Здесь можно было пойти длинным путем: возвести  в куб, возвести
в куб, возвести  в куб, потом разделить числитель и знаменатель на «эн» в старшей степени. Но в данном случае есть более эффективное решение: можно почленно поделить числитель и знаменатель прямо под степенью-константой. Для устранения неопределенности делим числитель и знаменатель на
в куб, потом разделить числитель и знаменатель на «эн» в старшей степени. Но в данном случае есть более эффективное решение: можно почленно поделить числитель и знаменатель прямо под степенью-константой. Для устранения неопределенности делим числитель и знаменатель на  (старшую степень).
(старшую степень).
(5) Собственно выполняем почленное деление, и указываем слагаемые, которые стремятся к нулю.
(6) Доводим ответ до ума, помечаем, что  и делаем вывод о том, что ряд расходится
и делаем вывод о том, что ряд расходится
|
|
|
Билет 7 Теорема Лейбница для числовых рядов
Признак Лейбница: Если члены знакочередующегося ряда монотонно убывают по модулю, то ряд сходится.
Или в два пункта:
1) Ряд является знакочередующимся.
2) Члены ряда убывают по модулю:  . Причём, убывают монотонно.
. Причём, убывают монотонно.
Если выполнены оба условия, то ряд сходится.
Краткая справка о модуле приведена в методичке Горячие формулы школьного курса математики, но для удобства ещё раз:
Что значит «по модулю»? Модуль, как мы помним со школы, «съедает» знак «минус». Вернемся к ряду  . Мысленно сотрём ластиком все знаки и посмотрим на числа. Мы увидим, что каждый следующий член ряда меньше, чем предыдущий. Таким образом, следующие фразы обозначают одно и то же:
. Мысленно сотрём ластиком все знаки и посмотрим на числа. Мы увидим, что каждый следующий член ряда меньше, чем предыдущий. Таким образом, следующие фразы обозначают одно и то же:
– Члены ряда без учёта знака убывают.
– Члены ряда убывают по модулю.
– Члены ряда убывают по абсолютной величине.
– Модуль общего члена ряда стремится к нулю: 
Монотонность – это скучное постоянство.
Члены ряда строго монотонно убывают по модулю, если КАЖДЫЙ СЛЕДУЮЩИЙ член ряда по модулю МЕНЬШЕ, чем предыдущий:  . Для ряда
. Для ряда  выполнена строгая монотонность убывания, её можно расписать подробно:
выполнена строгая монотонность убывания, её можно расписать подробно:

А можно сказать короче: каждый следующий член ряда по модулю меньше, чем предыдущий:  .
.
Члены ряда нестрого монотонно убывают по модулю, если КАЖДЫЙ СЛЕДУЮЩИЙ член ряда по модулю НЕ БОЛЬШЕ предыдущего:  . Рассмотрим ряд с факториалом:
. Рассмотрим ряд с факториалом:  Здесь имеет место нестрогая монотонность, так как первые два члена ряда одинаковы по модулю. То есть, каждый следующий член ряда по модулю не больше предыдущего:
Здесь имеет место нестрогая монотонность, так как первые два члена ряда одинаковы по модулю. То есть, каждый следующий член ряда по модулю не больше предыдущего: 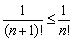 .
.
В условиях теоремы Лейбница должна выполняться монотонность убывания (неважно, строгая или нестрогая). Кроме того, члены ряда могут даже некоторое время возрастать по модулю, но «хвост» ряда обязательно должен быть монотонно убывающим.
|
|
|
|
|
|


