Пример сравнения средних арифметических, расчёта и построения доверительного интервала.

 

1. В физическом воспитании и спорте часто приходится делать вывод об общих закономерностях проявления какого-либо показателя: нормально или нет распределены результаты измерений этого показателя в генеральной совокупности, отличается ли среднее арифметическое значение результатов измерения в генеральной совокупности после тренировок от аналогичного параметра до тренировок, а обнаруженное расхождение между результатами не выходит за пределы случайных ошибок (эффективна или нет методика тренировок), отличается ли дисперсия генеральной совокупности результатов измерения показателя после тренировок от такого же показателя до тренировок (изменилась или нет стабильность результатов спортсмена) и т.д.

Так как указанные выводы делаются на основании относительно небольшого числа результатов измерения показателя (n = 30), необходима проверка достоверности (бесспорности) таких выводов.

Для этого применяются статистические гипотезы.

Статистической гипотезой называется предположение о свойстве генеральной совокупности, которое можно проверить, опираясь на данные выборки. Статистическую гипотезу обозначают символом H.

Обычно выдвигают и проверяют две противоречащие друг другу гипотезы:

1) нулевую (основную) H₀;

2) конкурирующую (альтернативную) H₁.

Примеры статистических гипотез:

1) Нулевая гипотеза H₀: закон распределения результатов измерения является нормальным. Конкурирующая гипотеза H₁: закон распределения результатов измерения отличен от нормального.

2) Нулевая гипотеза H₀: среднее арифметическое значение генеральной совокупности результатов измерения показателя после цикла тренировок не изменилось. Конкурирующая гипотеза H₁: среднее арифметическое значение увеличилось.

2. Для проверки выдвинутых нулевых гипотез применяют статистические критерии, разработанные математиками и носящие, как правило, их имена.

Статистическим критерием называют определенное правило, задающее условия, при которых проверяемую нулевую гипотезу следует либо отклонить, либо принять. При отклонении нулевой гипотезы принимается конкурирующая. Критерий обозначается буквой К.

Значение критерия, вычисленное по данным выборки, называют наблюдаемым значением критерия (К_набл). Совокупность значений критерия, при которых отвергают нулевую гипотезу, называют критической областью. Совокупность значений критерия, при которых нулевую гипотезу принимают, называют областью принятия гипотезы (областью допустимых значений). Указанные области разграничены критическим (граничным) значением критерия, который находится по соответствующей таблице.

Односторонняя критическая область используется, если, согласно конкурирующей гипотезе, одна рассматриваемая величина может быть только больше (или только меньше) другой величины.

Двусторонняя критическая область используется, если, согласно конкурирующей гипотезе, одна рассматриваемая величина может быть как больше, так и меньше (не равна) другой.

Отклонение нулевой гипотезы, когда она фактически верна, называется ошибкой первого рода. Принятие нулевой гипотезы, когда фактически она не верна, называется ошибкой второго рода.

Уровень значимости a – это вероятность попадания критерия К в критическую область, если верна нулевая гипотеза, другими словами, уровень значимости – это вероятность ошибки первого рода. Он служит для определения по таблицам критических значений критерия (К_крит), которые указывают положение критических точек, отделяющих критическую область от области принятия гипотезы. Обычно величина a выбирается малой. Поэтому попадание критерия К в критическую область при справедливости нулевой гипотезы мало вероятно. В этом случае, при попадании критерия К в критическую область считают, что должна быть принята конкурирующая гипотеза.

Часто a принимают равной 0,05. Это означает, что вероятность ошибочно принять гипотезу H₁, если справедлива гипотеза H₀, равна только
5 %.

Сформулируем основные этапы проверки статистических гипотез:

1) Исходя из задач исследования, формулируются статистические гипотезы.

2) Выбирается уровень значимости, на котором будут проверяться гипотезы.

3) На основе выборки, полученной из результатов измерения, определяется статистическая характеристика гипотезы.

4) Определяется критическое значение статистического критерия по соответствующей таблице на основании выбранного уровня значимости и объема выборки.

5) Вычисляется наблюдаемое (фактическое) значение статистического критерия.

6) На основе сравнения наблюдаемого и критического значения критерия в зависимости от результатов проверки нулевая гипотеза либо принимается, либо отклоняется в пользу альтернативной.

Для проверки статистических гипотез используются параметрические и непараметрические методы.

Параметрические методы служат для проверки гипотез о неизвестных параметрах генеральной совокупности, когда закон распределения случайной величины известен.

Непараметрические методы применяются в тех случаях, когда закон распределения случайной величины неизвестен, или когда условия применения параметрических методов не выполняются.

Параметрические методы эффективнее непараметрических.

Перейдем к ознакомлению с основными положениями теории надежности тестов.

3. В математической статистике разработан ряд критериев (параметрических и непараметрических) для сравнения средних арифметических.

Выбор критерия зависит от следующих условий:

1) объёма выборки (большие или малые);

2) законов распределения исследуемых совокупностей (нормальные, другие);

3) степени независимости выборок (зависимые, независимые);

4) известны или неизвестны генеральные дисперсии;

5) одинаковы или различны генеральные дисперсии;

6) возможна ли количественная или только качественная оценка рассматриваемого явления.

К параметрическим критериям для сравнения двух средних арифметических относятся критерии t для независимых и попарно зависимых выборок, имеющие распределение Стьюдента, а также критерий z, имеющий нормальное распределение. Последний разработан для сравнения двух средних арифметических независимых нормальных генеральных совокупностей, дисперсии которых известны. Так как в задачах из области физической культуры и спорта дисперсии генеральных совокупностей обычно неизвестны, критерий z для малых выборок не используется. Его рекомендуется использовать в качестве приближённого критерия для сравнения больших независимых выборок, имеющих любой закон распределения, так как для больших выборок (n ≥30) выборочные средние арифметические распределены приближённо нормально, а выборочные дисперсии приближённо равны генеральным дисперсиям.

Из существующих непараметрических критериев наиболее мощными являются X-критерий Ван дер Вардена для независимых выборок и U-критерий Уилкоксона для попарно зависимых выборок.

При сравнении средних независимых выборок рекомендуется поступать следующим образом:

1) Каждая в отдельности выборка проверяется на нормальность распределения по критерию Шапиро и Уилка

.

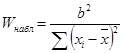В случае, если обе выборки распределены нормально, следует переходить к следующему пункту, в противном случае – к п. 4.

2) Сравниваются дисперсии выборок

.

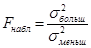В случае равенства дисперсий следует переходить к следующему пункту, в противном случае – к п. 4.

3) Для сравнения средних арифметических используется критерий Стьюдента

.

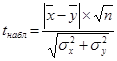Сравнение окончено.

4) Для сравнения средних арифметических используется критерий Ван дер Вардена

.

Сравнение окончено.

При сравнении средних попарно зависимых выборок рекомендуется поступать следующим образом:

1) Составляется выборка разностей парных значений .

2) Составленная выборка проверяется на нормальность распределения по критерию Шапиро и Уилка. В случае, если выборка распределена нормально, переходим к следующему пункту, в противном случае – к п. 4.

3) Для сравнения средних арифметических используется критерий Стьюдента

.

Сравнение окончено.

4) Для сравнения средних арифметических используется U-критерий Уилкоксона. Сравнение окончено.

4. По найденным характеристикам выборки судят о неизвестных характеристиках генеральной совокупности. Очевидно, что в общем случае они не будут точно совпадать друг с другом: истинное значение характеристики Q может быть больше или меньше выборочного значения характеристики Q*.

Чтобы статистически оценить искомое истинное значение характеристики Q, поступают следующим образом:

1) Задаются некоторой достаточно большой вероятностью p (например, p = 0,9; 0,95; 0,99; 0,999), чтобы событие, заключающееся в нахождении искомого значения Q с этой вероятностью в соответствующем интервале можно было считать статистически достоверным. Эту вероятность называют доверительной вероятностью. В спортивных исследованиях обычно принимают p = 0,95 (иногда 0,99).

2) Затем для заданной величины p рассчитывают по формулам математической статистики нижнюю Q₁ и верхнюю Q₂ границы интервала J_p.

Доверительным интервалом J_p называют случайный интервал (Q₁, Q₂), который накрывает неизвестную характеристику Q с доверительной вероятность p.

Границы доверительного интервала J_p называют:

Q₁ = Q* - e₁¾нижней доверительной границей;

Q₂ = Q* - e₂¾верхней доверительной границей.

Значения e₁ и e₂ могут совпадать (при симметричном распределении Q*) и быть разными (при несимметричном распределении Q*). Они характеризуют точность, а вероятность p¾надежность определения Q. Между надежностью и точностью существует обратная зависимость: чем выше надежность, тем ниже точность определения Q и наоборот.

С увеличением числа измерений при заданном p повышается точность определения Q (уменьшаются e₁ и e₂).

Для точного расчета границ доверительного интервала необходимо знать закон распределения выборочной характеристики Q*.

Задача определения доверительных интервалов для оценки генерального среднего арифметического значения x_г нормального распределения решена математической статистикой для следующих двух случаев:

а) генеральная дисперсия известна;

б) генеральная дисперсия неизвестна.

Рассмотрим второй случай.

В этом случае искомое генеральное среднее арифметическое находится в следующем доверительном интервале:

,

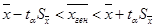где – среднее арифметическое значение выборки; t_a – величина, которая находится по таблицам распределения Стьюдента в зависимости от числа степеней свободы k = n - 1, уровня значимости a; – стандартная ошибка среднего арифметического, рассчитывается по формуле:

.

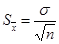Примечание: В практике научных исследований, когда закон распределения малой выборочной совокупности (n < 30) неизвестен или отличен от нормального, пользуются вышеприведенной формулой для приближенной оценки доверительных интервалов.

5. Для рассмотрения этого вопроса используется пример с двумя группами велосипедистов, прошедших подготовку с использованием разных методик (Гинзбург Г.И., Киселев В.Г. Расчетно-графические работы по спортивной метрологии. – Минск: БГОИФК, 1984. – С. 38 – 43)

 

Контрольные вопросы для самопроверки:

1. Что называют статистической гипотезой?

2. Принцип выдвижения статистических гипотез.

3. В чём заключается основной принцип проверки статистических гипотез?

4. Односторонняя и двусторонняя критическая область.

5. Ошибки при проверке гипотез. Уровень значимости.

6. Основные этапы проверки статистических гипотез.

7. Параметрические и непараметрические методы проверки статистических гипотез.

8. Какие условия определяют выбор критерия для сравнения средних арифметических двух выборок?

9. Какие параметрические и непараметрические критерии используются для сравнения средних арифметических двух выборок?

10. Какие критерии в каких случаях используются для сравнения средних независимых выборок?

11. Какие критерии в каких случаях используются для сравнения средних попарно зависимых выборок?

12. Что такое доверительный интервал, доверительная вероятность?

13. Порядок построения доверительного интервала.

14. В каких случаях можно точно определить границы доверительного интервала?

 

Литература:

1. Основы математической статистики. Уч. пособие для ин-тов физической культуры (под общ. ред. В.С. Иванова). – М.: Физкультура и спорт, 1990. – С. 74 – 78, 81 – 103.

2. Рукавицына С.Л., Волков Ю.О., Солтанович Л.Л. Спортивная метрология. Проверка эффективности методики тренировки с применением методов математической статистики. Практикум для студентов БГУФК. – Минск: БГУФК, 2006. – С. 49 – 51, 62, 67 – 68.

3. Гинзбург Г.И., Киселев В.Г. Расчетно-графические работы по спортивной метрологии. – Минск: БГОИФК, 1984. – С. 34 – 51.

 

 

ЛЕКЦИЯ 6.

 

Тема: Математико-статистические основы теории тестов.

 

Вопросы для рассмотрения:

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: