 |
Силы в механике (трение, тяготение, упругость). Закон всемирного тяготения.
|
|
|
|
1) Сила трения
Сила трения скольжения возникает при скольжении данного тела по поверхности другого: 
где  – коэффициент трения скольжения, зависящий от природы и состояния трущихся поверхностей;
– коэффициент трения скольжения, зависящий от природы и состояния трущихся поверхностей;  – сила нормального давления, прижимающая трущиеся поверхности друг к другу. Сила трения направлена по касательной к трущимся поверхностям в сторону, противоположную движению данного тела относительно другого.
– сила нормального давления, прижимающая трущиеся поверхности друг к другу. Сила трения направлена по касательной к трущимся поверхностям в сторону, противоположную движению данного тела относительно другого.
2) Сила тяготения (гравитационная сила)
Согласно закону всемирного тяготения любые две материальные точки притягиваются друг к другу с силой, пропорциональной произведению их масс ( и
и  ) и обратно пропорциональной квадрату расстояния
) и обратно пропорциональной квадрату расстояния  между ними
между ними 
где 
 – гравитационная постоянная.
– гравитационная постоянная.
Сила притяжения тела к Земле называется силой тяжести  . Под действием одной только силы тяжести тело, поднятое над поверхностью Земли, свободно падает на неё. Следовательно,
. Под действием одной только силы тяжести тело, поднятое над поверхностью Земли, свободно падает на неё. Следовательно,

3) Сила упругости возникает в результате взаимодействия тел, сопровождающегося их деформацией. Она пропорциональна смещению  частиц тела из положения равновесия и направлена к равновесному положению. Примером является сила упругой деформации пружины при растяжении или сжатии:
частиц тела из положения равновесия и направлена к равновесному положению. Примером является сила упругой деформации пружины при растяжении или сжатии: 
где  – жёсткость пружины;
– жёсткость пружины;  – упругая деформация.
– упругая деформация.
Закон всемирного тяготения

где 
 – гравитационная постоянная
– гравитационная постоянная
5) Закон сохранения импульса в механике
В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой


|
6) Момент инерции твердого тела. Теорема Штейнера.
Момент инерции тела – величина, определяющая его инертность во вращательном движении.
Моментом инерции твёрдого тела относительно некоторой плоскости называют скалярную величину, равную сумме произведений массы каждой точкитела на квадрат расстояния от этой точки до рассматриваемой плоскости.
|
|
|

теорема Штейнера: момент инерции тела  относительно произвольной оси равен сумме момента инерции
относительно произвольной оси равен сумме момента инерции  тела относительно оси, проходящей через центр масс, параллельно данной оси, и произведения массы тела
тела относительно оси, проходящей через центр масс, параллельно данной оси, и произведения массы тела  на квадрат расстояния
на квадрат расстояния  между этими осями
между этими осями 
7) Момент силы. Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси.
Момент силы - векторнаяфизическая величина, равная векторному произведению радиус-вектора, проведённого от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
 , где
, где  – радиус-вектор точки приложения силы
– радиус-вектор точки приложения силы
Модуль момента силы определяется выражением:
 где
где  - плечо силы
- плечо силы
Основное уравнение динамики вращательного движения твёрдого тела вокруг неподвижной оси: угловое ускорение тела, вращающегося вокруг неподвижной оси, прямо пропорционально моменту приложенной силы относительно этой оси и обратно пропорционально моменту инерции тела относительно этой же оси.
 или
или 
8. Кинетическая и потенциальная энергия. Закон сохранения энергии.
Энергия – универсальная количественная мера движения материи во всех формах этого движения. С различными формами движения материи связывают различные виды энергии: механическую, тепловую, электромагнитную и т.д.
Механическая энергия характеризует способность тела или системы тел совершать механическую работу. Различают два вида механической энергии: кинетическую  и потенциальную
и потенциальную  . Их сумма представляет собой полную механическую энергию
. Их сумма представляет собой полную механическую энергию  системы
системы  .
.
Кинетической энергией механической системы  называется энергия механического движения этой системы. Тело массой
называется энергия механического движения этой системы. Тело массой  , движущееся со скоростью
, движущееся со скоростью  обладает кинетической энергией
обладает кинетической энергией  .
.
|
|
|
Потенциальная энергия – часть механической энергии системы, зависящая только от её конфигурации, т. е. от взаимного расположения частей системы и от их положения во внешнем силовом поле.
1) потенциальная энергия тела массой  , поднятого на высоту
, поднятого на высоту 
 ;
;
2) потенциальная энергия пружины, растянутой на величину 
 ; 3)потенциальная энергия взаимодействия двух тел массами
; 3)потенциальная энергия взаимодействия двух тел массами  и
и  , находящихся на расстоянии
, находящихся на расстоянии  друг от друга
друг от друга  ;
;
4) потенциальная энергия взаимодействия двух заряженных тел с зарядами  и
и  , находящихся на расстоянии
, находящихся на расстоянии  друг от друга
друг от друга  .
.
Закон сохранения механической энергии – фундаментальный закон природы, вытекающий из симметрии пространства-времени.
Полная механическая энергия консервативной системы не изменяется с течением времени: 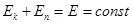 .
.
Энергия системы может переходить из одной формы в другую и перераспределяться между частями системы, но изменение полной энергии системы в любом процессе всегда равно энергии, полученной системой извне в этом процессе.
9. Момент импульса. Закон сохранения момента импульса.
Рассмотрим малый элемент твёрдого тела - материальную точку массой  . Её скорость
. Её скорость  и, соответственно, импульс
и, соответственно, импульс  направлены по касательной к траектории точки (окружности радиусом
направлены по касательной к траектории точки (окружности радиусом  ). Вектором момента импульса
). Вектором момента импульса  материальной точки относительно неподвижной точки
материальной точки относительно неподвижной точки  называется физическая величина, определяется векторным произведение
называется физическая величина, определяется векторным произведение  .
.

| Вектор момента импульса  материальной точки относительно оси материальной точки относительно оси  , представляет собой проекцию на эту ось вектора , представляет собой проекцию на эту ось вектора  . Он лежит на оси вращения и не имеет определённой точки приложения, его модуль определяется выражением . Он лежит на оси вращения и не имеет определённой точки приложения, его модуль определяется выражением
 Вектор момента импульса Вектор момента импульса  твёрдого тела относительно твёрдого тела относительно  равен сумме векторов равен сумме векторов  всех его точек. всех его точек.
|
Все векторы  лежат на оси вращения и направлены в одну сторону, поэтому и результирующий вектор
лежат на оси вращения и направлены в одну сторону, поэтому и результирующий вектор  лежит на оси
лежит на оси  , его модуль равен:
, его модуль равен:

 .
.
Уравнение можно записать в векторной форме:  . Продифференцировав по времени (при
. Продифференцировав по времени (при  ), получим:
), получим: 
 или
или  .
.
Это ещё одна форма записи основного уравнения динамики вращательного движения твёрдого тела относительно неподвижной оси: производная по времени от момента импульса  твёрдого тела относительно оси вращения равна моменту внешних сил
твёрдого тела относительно оси вращения равна моменту внешних сил  , действующих на тело, относительно той же оси. Изменение момента импульса вращающегося тела происходит под действием импульса момента внешних сил, действующих на него.
, действующих на тело, относительно той же оси. Изменение момента импульса вращающегося тела происходит под действием импульса момента внешних сил, действующих на него.
|
|
|
Закон сохранения момента импульса – фундаментальный закон, вытекающий из симметрии пространства-времени. В замкнутой системе момент внешних сил  равен нулю. Поэтому
равен нулю. Поэтому
 и
и  или
или 
10. Механические гармонические колебания. Дифференциальное уравнение механических гармонических колебаний.
Колебаниями называются движения или процессы, характеризующиеся повторяемостью во времени.
В зависимости от физической природы различают механические колебания, электромагнитные, электромеханические и др.
Свободные (собственные) колебания совершаются за счёт первоначально сообщённой энергии. Вынужденные колебания происходят под действием на систему внешней периодически изменяющейся силы.Механические колебания материальной точки называются гармоническими, если её смещение  из положения равновесия изменяется со временем по закону косинуса (синуса)
из положения равновесия изменяется со временем по закону косинуса (синуса)  , где
, где  – амплитуда колебаний (максимальное смещение точки из положения равновесия);
– амплитуда колебаний (максимальное смещение точки из положения равновесия);  – фаза колебания в момент времени
– фаза колебания в момент времени 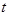 ;
;  – круговая (циклическая) частота;
– круговая (циклическая) частота;  – начальная фаза колебаний в момент времени
– начальная фаза колебаний в момент времени 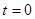 .
.

| Скорость и ускорение точки
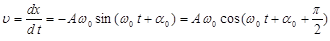 , ,
 совершают гармонические колебания с той же частотой
совершают гармонические колебания с той же частотой  , что и , что и  . Их амплитуды соответственно равны . Их амплитуды соответственно равны  и и  . Фаза скорости опережает фазу смещения на . Фаза скорости опережает фазу смещения на  , смещение и ускорение находятся в противофазе. , смещение и ускорение находятся в противофазе.
|
Уравнение, записанное как  , является дифференциальным уравнением механических гармонических колебаний с решением вида
, является дифференциальным уравнением механических гармонических колебаний с решением вида  .
.
11. Пружинный маятник. Математический маятник.
Гармоническим осциллятором называется система, закон движения которой описывается уравнением вида  . Примерами гармонического осциллятора являются пружинный, физический и математический маятники.
. Примерами гармонического осциллятора являются пружинный, физический и математический маятники.

| Пружинный маятник – груз массой  , подвешенный на абсолютно упругой пружине и совершающий колебания под действием квазиупругой силы: , подвешенный на абсолютно упругой пружине и совершающий колебания под действием квазиупругой силы:  ( (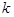 – жёсткость пружины). Закон движения маятника имеет вид: – жёсткость пружины). Закон движения маятника имеет вид: 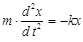 или или  . Пружинный маятник совершает гармонические колебания по закону . Пружинный маятник совершает гармонические колебания по закону
 , ,
|
циклическая частота и периодом которых равны:  и
и  .
.
|
|
|

| Математический маятник– материальная точка массой  , подвешенная на невесомой и нерастяжимой нити длиной , подвешенная на невесомой и нерастяжимой нити длиной  и колеблющаяся под действием силы тяжести без трения. и колеблющаяся под действием силы тяжести без трения.  - период маятника. Длина - период маятника. Длина  . .
|
12. Уравнение Клапейрона-Менделеева. Молярная масса, количество вещества.
Молярной массой (М) называют массу одного моля, т.е. массу такого количества вещества, которое содержит столько молекул или атомов, сколько атомов содержится в углероде массой 0,012 кг. Таким образом 1 моль любого вещества содержит одно и тоже число молекул, называемое числом Авогадро: NA = 6,022054(32) · 1023 моль-1.
Количество вещества — это число частиц вещества (атомов, молекул), выраженное в молях. Учитывая определение моля и числа Авогадро, можно сказать, что количество вещества v равно отношению числа молекул в данном теле к постоянной Авогадро NA, т.е. к числу молекул в 1 моле вещества: v = N/ NA.
Идеальным считается газ, который можно рассматривать как систему невзаимодействующих материальных точек, упруго сталкивающихся друг с другом и со стенками сосуда.
Уравнение состояния представляет собой функциональную зависимость, связывающую между собой термодинамические параметры:  Экспериментально установлено, что для 1 моля идеального газа выполняется уравнение Клапейрона:
Экспериментально установлено, что для 1 моля идеального газа выполняется уравнение Клапейрона:  ,
,
где  – молярный объём газа;
– молярный объём газа;  – универсальная газовая постоянная
– универсальная газовая постоянная  . Запишем уравнение (8.3) для массы
. Запишем уравнение (8.3) для массы  газа, занимающей объём
газа, занимающей объём  :
:  .
.
Это уравнение Менделеева – Клапейрона, называемое уравнением состояния идеального газа. Удобно пользоваться ещё одной формой уравнения состояния.  ,
,  ,
,
где  - число Авогадро (число частиц, содержащихся в 1 моле),
- число Авогадро (число частиц, содержащихся в 1 моле),  – постоянная Больцмана,
– постоянная Больцмана,  – концентрация молекул (число частиц газа, содержащихся в единичном объёме);
– концентрация молекул (число частиц газа, содержащихся в единичном объёме);
Отсюда следует, что при постоянной температуре давление газа прямо пропорционально концентрации его молекул.
13. Основное уравнение молекулярно-кинетической теории (МКТ) идеального газа. Средняя квадратичная скорость молекул газа.
При непрерывном и хаотичном движении молекулы газа упруго сталкиваются друг с другом и со стенками сосуда. Соударения молекул между собой приводят к перераспределению их скоростей и энергий. При ударе молекул о стенку возникает сила давления.
Основное уравнение кинетической теории идеального газа связывает макроскопический параметр  измеряемый экспериментально, и характеристики микрочастицы (
измеряемый экспериментально, и характеристики микрочастицы ( ):
):  где
где  - масса молекулы, где
- масса молекулы, где  – концентрация молекул;
– концентрация молекул;  – квадрат средне квадратичной скорости поступательного движения молекул газа (чаще её обозначают через
– квадрат средне квадратичной скорости поступательного движения молекул газа (чаще её обозначают через  ).
).
|
|
|
Средняя кинетическая энергия поступательного движения молекул газа
Основное уравнение кинетической теории идеального газа для давления можно записать так:  .
.
Давление равно  средней кинетической энергии поступательного движения молекул, заключённых в единичном объёме.
средней кинетической энергии поступательного движения молекул, заключённых в единичном объёме.
Следовательно, давление, рассматриваемое ранее как силовая характеристика, является также энергетической характеристикой.
Из верхних формул, можно получить выражение:  . Следовательно, средняя кинетическая энергия поступательного движения одной молекулы идеального газа
. Следовательно, средняя кинетическая энергия поступательного движения одной молекулы идеального газа  зависит только от его термодинамической температуры
зависит только от его термодинамической температуры  .
.
Отсюда, в области температур, далёких от 0оК, термодинамическая температура является мерой средней кинетической энергии поступательного движения молекул идеального газа.
14. Явления переноса в термодинамических системах: вязкость, диффузия, теплопроводность.
При появлении в объёме газа какой-либо неоднородности возникают потоки вещества, энергии или импульса упорядоченного движения частиц, приводящие к выравниванию пространственного распределения этой физической величины и устранению неоднородности. При этом протекают особые явления, называемые явлениями переноса. К этим явлениям относятся диффузия, теплопроводность и внутреннее трение.
Диффузия – явление самопроизвольного взаимного проникновения и перемешивания частиц двух соприкасающихся газов, жидкостей и даже твёрдых тел. При постоянной температуре явление диффузии заключается в переносе массы газа из мест, где его концентрация больше, в места, где она меньше.
Если в химически однородном газе концентрация n (или плотность  ) изменяется вдоль оси
) изменяется вдоль оси  , то перенос вещества вдоль этой оси описывается законом Фика:
, то перенос вещества вдоль этой оси описывается законом Фика:  где
где  – масса газа, диффундирующего за время
– масса газа, диффундирующего за время  через площадку
через площадку  , перпендикулярную направлению переноса,
, перпендикулярную направлению переноса,  – градиент (перепад) плотности вдоль оси
– градиент (перепад) плотности вдоль оси  ;
;  – коэффициент диффузии. Знак минус в формуле указывает на то, что перенос массы происходит в направлении убывания плотности
– коэффициент диффузии. Знак минус в формуле указывает на то, что перенос массы происходит в направлении убывания плотности  . Плотность потока массы
. Плотность потока массы  , (масса вещества, переносимая в единицу времени через единицу площади) равна
, (масса вещества, переносимая в единицу времени через единицу площади) равна  =
=  или
или  .
.
Из молекулярно-кинетической теории газов получено выражение для коэффициента диффузии  , где
, где  - средняя арифметическая скорость движения частиц,
- средняя арифметическая скорость движения частиц,  - средняя длина свободного пробега молекул.
- средняя длина свободного пробега молекул.
Внутреннее трение (вязкость) возникает между слоями газа или жидкости, движущимися параллельно друг другу с различными по модулю скоростями.
Пусть два слоя жидкости (1 и 2) движутся параллельно друг другу со скоростями  и и  , причём , причём  (рис.8.4). Благодаря хаотическому тепловому движению молекулы переходят из слоя в слой и «переносят» импульсы (рис.8.4). Благодаря хаотическому тепловому движению молекулы переходят из слоя в слой и «переносят» импульсы  своего упорядоченного движения. При переходе молекул из «быстрого» слоя 1 в «медленный» слой 2 своего упорядоченного движения. При переходе молекул из «быстрого» слоя 1 в «медленный» слой 2
|  Рис.8.4 Вязкость Рис.8.4 Вязкость
|
частицы переносят большие импульсы и соударения между молекулами приводят к ускорению упорядоченного движения слоя 2. И, наоборот, при переходе из «медленного» слоя 2 в «быстрый» слой 1 перешедшие частицы ускоряют своё упорядоченное движение. В результате этих процессов переноса импульса молекул между слоями 1 и 2 возникают силы внутреннего трения, которые определяются законом Ньютона:  .где
.где  – коэффициент внутреннего трения (динамическая вязкость);
– коэффициент внутреннего трения (динамическая вязкость);  – градиент скорости в направлении, перпендикулярном направлению движения слоёв);
– градиент скорости в направлении, перпендикулярном направлению движения слоёв);  – площадь трущихся слоев.
– площадь трущихся слоев.
Сила  считается положительной, если она ускоряет слой и отрицательной, если тормозит. Закон Ньютона можно записать и для импульса
считается положительной, если она ускоряет слой и отрицательной, если тормозит. Закон Ньютона можно записать и для импульса  , переносимого частицами при переходах между слоями
, переносимого частицами при переходах между слоями  .
.
Теплопроводность – это явление переноса теплоты от слоёв газа, с более высокой температурой, и, следовательно, более высоким значением энергии, к слоям с более низкой температурой. Хаотическое тепловое движение молекул приводит к направленному переносу внутренней энергии газа. Молекулы, попавшие из нагретых частей объёма газа в более холодные, отдают часть своей энергии окружающим частицам и наоборот.
Если температура газа изменяется вдоль оси  , то перенос внутренней энергии газа путём теплообмена вдоль этой оси описывается законом Фурье:
, то перенос внутренней энергии газа путём теплообмена вдоль этой оси описывается законом Фурье:  ,где
,где  – количество теплоты, которое передаётся путём теплопроводности за время
– количество теплоты, которое передаётся путём теплопроводности за время  через площадку
через площадку  , расположенную перпендикулярно направлению переноса внутренней энергии;
, расположенную перпендикулярно направлению переноса внутренней энергии;  – градиент температуры;
– градиент температуры;  – коэффициент теплопроводности. Знак минус в формуле указывает на то, что перенос внутренней энергии происходит в направлении убывания температуры. Количество теплоты, переносимое в единицу времени через единицу площади, т. е. плотность теплового потока
– коэффициент теплопроводности. Знак минус в формуле указывает на то, что перенос внутренней энергии происходит в направлении убывания температуры. Количество теплоты, переносимое в единицу времени через единицу площади, т. е. плотность теплового потока  , равна
, равна  =
=  или
или  .
.
С помощью молекулярно-кинетической теории получено выражение для коэффициента теплопроводности:  , где
, где  - средняя арифметическая скорость движения частиц,
- средняя арифметическая скорость движения частиц,  - средняя длина свободного пробега молекул,
- средняя длина свободного пробега молекул,  - плотность газа,
- плотность газа,  - удельная теплоёмкость газа при постоянном объёме (она определяет внутреннюю энергию вещества при данной температуре
- удельная теплоёмкость газа при постоянном объёме (она определяет внутреннюю энергию вещества при данной температуре  ).
).
15. Теплоемкости газов. Молярные теплоемкости при постоянном объеме и при постоянном давлении. Уравнение Майера.
Удельная теплоемкость вещества — величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К: с = mdT
Единицей удельной теплоемкости является джоуль на килограмм-кельвин [Дж/(кг-К)].
Молярная теплоемкость — величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К:  =
=  , где ν— количество вещества. Единица молярной теплоемкости — джоуль на моль-кельвин [ДжДмоль • К)].
, где ν— количество вещества. Единица молярной теплоемкости — джоуль на моль-кельвин [ДжДмоль • К)].
Удельная теплоемкость с связана с молярной  соотношением
соотношением  =cM, где М — молярная масса вещества.
=cM, где М — молярная масса вещества.
Различают теплоемкости при постоянном объеме и постоянном давлении, если в процессе нагревания вещества его объем или давление поддерживается постоянным.
Если газ нагревается при постоянном объеме, то работа внешних сил равна нулю и сообщаемая газу извне теплота идет только на увеличение его внутренней энергии:  т. е. молярная теплоемкость газа при постоянном объеме
т. е. молярная теплоемкость газа при постоянном объеме  равна изменению внутренней энергии 1 моль газа при повышении его температуры на 1 К.
равна изменению внутренней энергии 1 моль газа при повышении его температуры на 1 К.
Если газ нагревается при постоянном давлении, то выражение можно записать в виде  .
.
Учитывая, что  не зависит от вида процесса (внутренняя энергия идеального газа не зависит ни от р, ни от V, а определяется лишь температурой Т) и всегда равна
не зависит от вида процесса (внутренняя энергия идеального газа не зависит ни от р, ни от V, а определяется лишь температурой Т) и всегда равна  , и дифференцируя уравнение Клапейрона— Менделеева p
, и дифференцируя уравнение Клапейрона— Менделеева p  = RT по Т (р = const), получаем
= RT по Т (р = const), получаем  =
=  +R.
+R.
Выражение  =
=  +R. называется уравнением Майера; оно показывает, что
+R. называется уравнением Майера; оно показывает, что  всегда больше
всегда больше  на величину молярной газовой постоянной. Это объясняется тем, что при нагревании газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа.
на величину молярной газовой постоянной. Это объясняется тем, что при нагревании газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа.
16. Первое начало термодинамики. Внутренняя энергия системы. Работа и теплота.
Некоторая система (газ, заключенный в цилиндр под поршнем), обладая внутренней энергией  получила некоторое количество теплоты Q и, перейдя в новое состояние, характеризующееся внутренней энергией
получила некоторое количество теплоты Q и, перейдя в новое состояние, характеризующееся внутренней энергией  , совершила работу А над внешней средой, т. е. против внешних сил. Количество теплоты считается положительным, когда оно подводится к системе, а работа — положительной, когда система совершает ее против внешних сил. В соответствии с законом сохранения энергии при любом способе перехода системы из первого состояния во второе изменение внутренней энергии AU=
, совершила работу А над внешней средой, т. е. против внешних сил. Количество теплоты считается положительным, когда оно подводится к системе, а работа — положительной, когда система совершает ее против внешних сил. В соответствии с законом сохранения энергии при любом способе перехода системы из первого состояния во второе изменение внутренней энергии AU=  будет одинаковым и равным разности между количеством теплоты Q, полученным системой, и работой А, совершенной системой против внешних сил: AU = Q - А, или Q=ΔU+A. Уравнение Q=ΔU+A выражает первое начало термодинамики: теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил.
будет одинаковым и равным разности между количеством теплоты Q, полученным системой, и работой А, совершенной системой против внешних сил: AU = Q - А, или Q=ΔU+A. Уравнение Q=ΔU+A выражает первое начало термодинамики: теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил.
Если система периодически возвращается в первоначальное состояние, то изменение ее внутренней энергии AU=0. Тогда, согласно первому началу термодинамики, A=Q, т. е. вечный двигатель первого рода — периодически действующий двигатель, который совершал бы большую работу, чем сообщенная ему извне энергия, невозможен (одна из формулировок первого начала термодинамики).
Полную работу А, совершаемую газом при изменении его объема от  до
до  , найдем интегрированием формулы A=pΔV.
, найдем интегрированием формулы A=pΔV.
 . Результат интегрирования определяется характером зависимости между давлением и объемом газа. Найденное для работы выражение
. Результат интегрирования определяется характером зависимости между давлением и объемом газа. Найденное для работы выражение  справедливо при любых изменениях объема твердых, жидких и газообразных тел.
справедливо при любых изменениях объема твердых, жидких и газообразных тел.
17. Изопроцессы. Изохорный, изобарный, изотермический, адиабатический, политропный процессы.
Среди равновесных процессов, происходящих с термодинамическими системами, выделяются изопроцессы, при которых один из основных параметров состояния сохраняется постоянным.
Изохорный процесс (V=const). График зависимости между параметрами состояния идеального газа при V=const называется изохорой. Изохора в координатах р, V изображается прямой, параллельной оси ординат (рис. 1), где процесс 1 — 2 есть изохорное нагревание, а 3 — 4 — изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т. е.
δА=pdV=0.
рис. 1  Из первого начала термодинамики (Q = ΔU + А) для изохорного процесса следует, что вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии: Q=ΔA.
Из первого начала термодинамики (Q = ΔU + А) для изохорного процесса следует, что вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии: Q=ΔA.
Изобарный процесс (р = const). График зависимости между параметрами состояния идеального газа при р = const называется изобарой. Изобара в координатах р, V изображается прямой, параллельной оси V (рис.2). При изобарном процессе работа газа


Рис.2. 
Изотермический процесс (Т=const). Изотермический процесс описывается законом Бойля — Мариотта: pV= const. График зависимости между параметрами состояния идеального газа при Т = const называется изотермой. Изотерма в координатах р, V представляет собой гиперболу (рис.3), расположенную на диаграмме тем выше, чем выше температура, при которой происходит процесс.
Рис.3. 
Работа изотермического расширения газа: 
Так как при Т = const внутренняя энергия идеального газа не изменяется:  . Все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил:
. Все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил: 
Адиабатным называется процесс, при котором отсутствует теплообмен между системой и окружающей средой (Q = 0). Из первого начала термодинамики для адиабатного процесса следует, что А= - ΔU, т. е. внешняя работа совершается за счет изменения внутренней энергии системы.
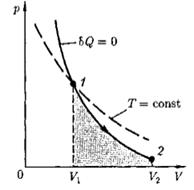 График зависимости между параметрами состояния идеального газа при Q =.0 называется адиабатой.
График зависимости между параметрами состояния идеального газа при Q =.0 называется адиабатой.
Процесс, в котором теплоемкость остается постоянной, называется политропным. Исходя из первого начала термодинамики при условии постоянства теплоемкости (С=const), можно вывести уравнение политропы:
p  =const, где n=
=const, где n=  – показатель политропы.
– показатель политропы.
18. Цикл Карно. Тепловые машины и их КПД.
Из формулировки второго начала термодинамики по Кельвину следует, что вечный двигатель второго рода — периодически действующий двигатель, совершающий работу за счет охлаждения одного источника теплоты, — невозможен. Для иллюстрации этого положения рассмотрим работу теплового двигателя.
Принцип действия теплового двигателя: от термостата с более высокой температурой  называемого нагревателем, за цикл отбирается количество теплоты
называемого нагревателем, за цикл отбирается количество теплоты  а термостату с более низкой температурой
а термостату с более низкой температурой  , называемому холодильником, за цикл передается количество теплоты
, называемому холодильником, за цикл передается количество теплоты  , при этом совершается работа А =
, при этом совершается работа А =  -
-  .
.
Чтобы термический коэффициент полезного действия теплового двигателя был равен 1, необходимо выполнение условия Q2 = 0, т. е. тепловой двигатель должен был бы иметь один источник теплоты. Однако, согласно Карно, для работы теплового двигателя необходимо не менее двух источников теплоты с различными температурами, иначе это противоречило бы второму началу термодинамики.
Без совершения работы нельзя отбирать теплоту от менее нагретого тела и отдавать ее более нагретому. Это утверждение есть не что иное, как второе начало термодинамики в формулировке Клаузиуса.
Цикл Карно — цикл, состоящий из четырех последовательных обратимых процессов: изотермического расширения, адиабатного расширения, изотермического сжатия и адиабатного сжатия.
Прямой цикл Карно изображен на рис. 3, где изотермические расширение и сжатие заданы соответственно кривыми 1 — 2 и З — 4, а адиабатные расширение и сжатие — кривыми 2—3 и 4—1.
Рис.3. 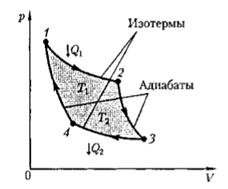
Термический КПД цикла Карно: 

т. е. для цикла Карно КПД действительно определяется только температурами нагревателя и холодильника (доказательство теоремы Карно).
19. Второе начало термодинамики.
Первое начало термодинамики, выражая закон сохранения и превращения энергии, не позволяет установить направление протекания термодинамических процессов. Появление второго начала термодинамики связано с необходимостью дать ответ на вопрос, какие процессы в природе возможны, а какие нет. Второе начало термодинамики определяет направление протекания термодинамических процессов.
Краткая формулировка второго начала термодинамики: в процессах, происходящих в замкнутой системе, энтропия не убывает (Закон возрастания энтропии). Второе начало термодинамики – теплота не может самопроизвольно переходить от тела менее нагретого к телу более нагретому. Под теплотой понимается внутренняя энергия тела.
Укажем еще две формулировки второго начала термодинамики:
1) по Кельвину: невозможен круговой прогресс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу;
2) по Клаузиусу: невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому.
20. Элементарный электрический заряд. Закон сохранения электрического заряда. Закон Кул
|
|
|


