Главная | Обратная связь | Поможем написать вашу работу!

Методические указания к выполнению работы. Примеры расчета

3.1. Задача №1. Определение напряжений в грунте от действия
сосредоточенных сил

Для случая, когда к горизонтальной поверхности массива грунта приложено несколько сосредоточенных сил , величины вертикальных составляющих напряжений в любой точке массива грунта можно определить суммированием составляющих напряжений от действия каждой силы в отдельности с использованием зависимости

, (3.1.1)

где 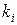- коэффициент, являющийся функцией отношения ;

- расстояние по горизонтальной оси от рассматриваемой точки до оси , проходящей через точку приложения сосредоточенной силы ;

- глубина рассматриваемой точки от плоскости приложения сосредоточенной силы .

Значения коэффициента приведены в табл.4.1 [2], табл.3.1 [5] или в таблице 1.1 приложения настоящих методических указаний.

При построении расчетной схемы и эпюр напряжений следует принимать масштаб расстояний 1:50, масштаб напряжений 0,05 МПа в 1 см.

Пример расчета

Дано:

Решение. Определяем напряжения в точках, расположенных по вертикали I-I.

Точка 1 z=1 м.

r₁=2 м r₁/z=2/1=2 k₁=0,0085

r₂=0 r₂/z=0/1=0 k₂=0,4775

r₃=3 м r₃/z=3/1=3 k₃=0,0015

Точка 2 z=2 м.

r₁=2 м r₁/z=2/2=1 k₁=0,0844

r₂=0 r₂/z=0/2=0 k₂=0,4775

r₃=3 м r₃/z=3/2=1,5 k₃=0,0251

Точка 3 z=3 м.

r₁=2 м r₁/z=2/3=0,6667 k₁=0,1889

r₂=0 r₂/z=0/3=0 k₂=0,4775

r₃=3 м r₃/z=3/3=1 k₃=0,0844

Точка 4 z=4 м.

r₁=2 м r₁/z=2/4=0,5 k₁=0,2733

r₂=0 r₂/z=0/4=0 k₂=0,4775

r₃=3 м r₃/z=3/4=0,75 k₃=0,1565

Точка 5 z=6 м.

r₁=2 м r₁/z=2/6=0,33 k₁=0,3687

r₂=0 r₂/z=0/6=0 k₂=0,4775

r₃=3 м r₃/z=3/6=0,5 k₃=0,2733

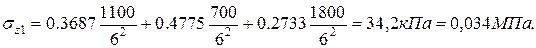
Определяем напряжения в точках расположенных по горизонтали II-II.

Точка 6 z=3 м.

r₁=1 м r₁/z=1/3=0,33 k₁=0,3687

r₂=3 м r₂/z=3/3=1 k₂=0,0844

r₃=6 м r₃/z=6/3=2 k₃=0,0085

Точка 7 z=3 м.

r₁=1 м r₁/z=1/3=0,33 k₁=0,3687

r₂=1 м r₂/z=1/3=0,33 k₂=0,3687

r₃=4 м r₃/z=4/3=1,33 k₃=0,0374

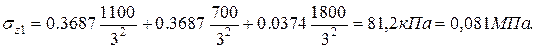
Точка 8 z=3 м.

r₁=3 м r₁/z=3/3=1 k₁=0,0844

r₂=1 м r₂/z=1/3=0,33 k₂=0,3687

r₃=2 м r₃/z=2/3=0,67 k₃=0,1889

Точка 9 z=3 м.

r₁=5 м r₁/z=5/3=1,67 k₁=0,0171

r₂=3 м r₂/z=3/3=1 k₂=0,0844

r₃=0 r₃/z=0/3=0 k₃=0,4775

По полученным значениям напряжений строим эпюры распределения напряжений по соответствующим точкам (рис.3.1).

Рис. 3.1. Эпюры напряжений

Задача №2.

Определение напряжений в грунте методом угловых точек

Распределение по глубине вертикальных составляющих напряжений в любой точке массива грунта от действия равномерно распределенной нагрузки в пределах или за пределами плит нагружения может быть определено по методу угловых точек по формуле

, (3.2)

где - коэффициент, определяемый в зависимости от отношения сторон прямоугольной площади загружения ( – длинная ее сторона, – ее ширина) и отношения ( - глубина, на которой определяется напряжение );

- интенсивность равномерно распределенной нагрузки.

В соответствии с этим заданные плиты нагружения разбивают на прямоугольники таким образом, чтобы они имели общую угловую точку, через которую проходит расчетная вертикаль . Для каждого из этих прямоугольников со сторонами с помощью таблиц определяют значения коэффициента и, пользуясь принципом независимости действия сил, находят алгебраическим суммированием напряжения в заданных точках массива. Значения коэффициента приведены в табл.3.5 [5] и в табл.1.2 приложения настоящих методических указаний.

Масштаб расстояний 1:50, масштаб напряжений 0,05 МПа в 1 см.

Пример расчета

Дано: 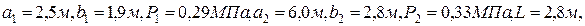расчетная вертикаль М₃.

Решение. Заданные плиты нагружения разбиваем на прямоугольники таким образом, чтобы они имели общую угловую точку, через которую проходит расчетная вертикаль М₃ (рис. 2.2). Таким образом, имеем 5 прямоугольников:

Искомые напряжения найдем, суммируя напряжения от действия нагрузки по прямоугольникам 1, 2, 3 взятым со знаком «плюс» и напряжения от действия нагрузки по прямоугольникам 4, 5 со знаком «минус».

z=1 м

1. 2,5/1,9=1,32, 1/1,9=0,53, 0,2352.

2. 1,31, 0,31, 0,2457.

3. 1,86, 0,57, 0,232.

4. 9,44, 2,22, 0,128.

5. 3,89, 2,22, 0,1251.

z=2 м

1. 1,32, 1,06, 0,1782.

2. 1,31, 0,62, 0,2286.

3. 1,86, 1,14, 0,1983.

4. 9,44, 4,4, 0,069.

5. 3,89, 4,4, 0,0597.

z=4 м

1. 1,32, 2,11, 0,0933.

2. 1,31, 1,23, 0,1654.

3. 1,86, 2,28, 0,1009.

4. 9,44, 8,89, 0,0316.

5. 3,89, 8,89, 0,0199.

z=6 м

1. 1,32, 3,16, 0,0508.

2. 1,31, 1,85, 0,1013.

3. 1,86, 3,43, 0,0571.

4. 9,44, 13,3, 0,0155.

5. 3,89, 13,3, 0,0084.

По полученным значениям напряжений строим эпюру распределения напряжений (рис.3.2).

Рис.3.2. Эпюра напряжений

Задача №3.

Определение напряжений в грунте от действия
равномерно распределенной нагрузки

Для случая действия на поверхности массива грунта нагрузки, распределенной в пределах гибкой полосы по трапециевидной эпюре, величину вертикального сжимающего напряжения в заданной точке массива грунта определяют путем суммирования напряжений от прямоугольного и треугольного элементов эпюры внешней нагрузки.

Вертикальные напряжения , возникающие от действия полосообразной равномерно распределенной нагрузки (прямоугольный элемент эпюры внешней нагрузки), определяют по формуле:

, (3.3.1)

где - коэффициент, определяемый в зависимости от величины относительных координат и , табл. 1.3 приложения 1 настоящих методических указаний;

– вертикальная равномерно распределенная нагрузка.

Вертикальные напряжения , возникающие от действия полосообразной неравномерной нагрузки, распределенной по закону треугольника (треугольный элемент эпюры внешней нагрузки), определяются по формуле

, (3.3.2)

где - коэффициент, определяемый в зависимости от величины относительных координат и , табл. 1.4 приложения 1 настоящих методических указаний;

Р – наибольшая ордината треугольной нагрузки.

Пример расчета

Дано: расчетная вертикаль М₅.

Решение. При расчете вертикальных напряжений равномерно распределенную нагрузку принимаем , при этом наибольшая ордината треугольной нагрузки . Начало координат для равномерно распределенной нагрузки находится в середине полосы нагружения, а начало координат для неравномерно распределенной нагрузки находится с краю полосы нагружения, где значение треугольной нагрузки равно нулю.