Краткие теоретические сведения

1. Вычислить вторую производную функции ;
2. Найти у функции критические точки 2-го рода, т.е. точки в которых или не существует;

1. Исследовать знак второй производной функции в интервалах, на которые разбивается область определения функции критическими точками 2-го рода;
2. Если в рассматриваемом интервале

, то на этом интервале график функции выпуклый вверх;

, то на этом интервале график функции выпуклый вниз;

1. Если - критическая точка 2-го рода и при переходе через нее меняет знак, то - точка перегиба.

Пример. Исследовать функцию и построить ее график.

Решение: исследуем функцию по схеме:

1. D(y)=R;

2. - функция не будет ни четной, ни нечетной; функция непериодическая;

3. Найдем точки пересечения с (ОХ): . Перебирая делители свободного члена, находим целые нули функции: .

Найдем точки пересечения графика функции с осью (ОУ): если , то ;

4. Асимптот нет;

5. Для нахождения интервалов монотонности функции найдем ее производную:

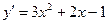. Найдем критические точки функции: . Получим: . Найдем интервалы возрастания и убывания функции:

Из чертежа имеем, что функция возрастает на , убывает на . Найдем экстремумы функции:

. Значит, точка максимума имеет координаты

. Значит, точка минимума имеет координаты

6. Для нахождения интервалов выпуклости графика функции вычислим вторую

производную: 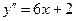. Найдем критические точки 2 рода функции:

. Определим знак второй производной в интервалах, на которые разбивается область определения

Значит, график функции будет выпуклым вверх на и выпуклым вниз на . Т.к. вторая производная меняет знак при переходе через точку , то в ней график будет иметь перегиб. Вычислим: 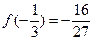. Значит, точка перегиба .

7. Построим график:

Пример. Построить график функции у =

Решение:

1. Найдем область определения функции. Она задается условиями x ≠ 1, x ≠ -1 (при значениях x ≠ 1, x ≠ -1 знаменатель дроби обращается в нуль). Итак,

D(f)=(-∞;1)(-1:1)(1;+∞).

2. Исследуем функцию на честность:

f f (x)

Значит, заданная функция четна, ее график симметричен относительно оси ординат, а потому можно для начала ограничиться построением ветвей графика при x ≥ 0.

3. Точек пересечения графика функции с осью ОХ нет,

Найдем точки пересечения графика функции с осью ОУ: если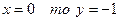

4. Найдем асимптоты графика. Вертикальной асимптотой является прямая x = 1, поскольку при этом значении x знаменатель дроби обращается в нуль, а числитель отличен от нуля. Для отыскания горизонтальной асимптоты надо вычислить f (x):

^.

Значит, y = 1 – горизонтальная асимптота графика функции.

5. Найдем критические точки, точки экстремума и промежутки монотонности функции:

y′ .

Критические точки найдем из соотношения y^´ = 0. Получаем –4x = 0, откуда находим,

что х = 0. При х < 0 имеем y^´ > 0, а при х > 0 имеем y^´ < 0. Значит, х = 0 – точка максимума функции, причем у_max = f (0)= .

При х > 0 имеем y^´ < 0, но следует учесть наличие точки разрыва х = 1. Значит, вывод о промежутках монотонности будет выглядеть так: на промежутке [0;1) функция убывает, на промежутке (1;+∞) функция также убывает.

1. Вычислим вторую производную

нигде не обращается в ноль, критическими точками будут только точки . Определим знак в интервалах:

7. Отметим (0;-1) – точку максимума, построим прямые у = 1 – горизонтальную асимптоту, что x = 1 и x = - 1– вертикальные асимптоты;