Главная | Обратная связь | Поможем написать вашу работу!

Дискретизация непрерывной модели

Содержание

Введение …………………………………………………………………………..3

Глава 1. Теоретическая часть.............................................................................4

1.1. Дискретная простейшая модель Вальраса – Эванса – Самуэльсона рынка одного товара ………………………………………………………...……. 4

1.2. Дискретизация непрерывной модели …………………………………… 5

1.3. Устойчивость дискретных систем ………………………………………. 7

1.2. Линейная модель Вальраса – Эванса - Самуэльсона рынка одного товара с кусочно-постоянным запаздыванием цены предложения……….…...…………8

Глава 2. Практическая часть.............................................................................10

2.1. Случай асимптотически устойчивой модели ………………………….….10

2.2. Случай устойчивой модели ……………………………………………..… 12

2.3. Случай неустойчивой модели ………………………………………….......14

Список использованной литературы...............................................................17

Введение

Данная работа посвящена исследованию устойчивости решений некоторых динамических моделей микро- и макроэкономики.

Цель данной работы – сравнить непрерывные и дискретные модели. Для достижения этой цели относительно каждой модели поставлены следующие задачи:

· Описать модель;

· Построить графики для непрерывных моделей;

· Провести дискретизацию;

· Записать условия устойчивости для дискретных моделей;

· Построить графики дискретных моделей;

· Сравнить непрерывные и дискретные модели.

В данной работе будет рассмотрена линейная модель Вальраса-Эванса-Самуэльсона рынка одного товара с кусочно-постоянным запаздыванием цены предложения.

Глава 1. Теоретическая часть

Динамическая непрерывная простейшая модель Вальраса – Эванса – Самуэльсона рынка одного товара.

Французский экономист Леон Вальрас - первый, кто взялся за построение модели общего равновесия. Особенность данной модели состоит в том, что рынок рассматривается автономно, т.е. без влияния внешних процессов.

Пусть P – это цена, D – спрос и S – предложение. Все функции являются непрерывными времени t. Функции спроса и предложения примут вид:

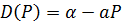; (1)

, (2)

где α, β, a, b = const.

Скорость роста цены пропорциональна дефициту товара на рынке с постоянным коэффициентом пропорциональности λ. Коэффициент отражает степень реакции, чувствительность покупателей на избыточный спрос. Модель имеет вид линейного обыкновенного дифференциального уравнения:

, (3)

Где – скорость изменения цены, составляет дефицит/профицит товара.

Подставим в уравнение (3) функции спроса (1) и предложения (2). Получим следующее уравнение:

. (4)

В точке равновесия 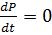, т.е. 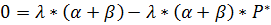, где 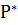- равновесная цена. Таким образом, получаем систему:

Вычтем из первого уравнения в системе второе и заменим 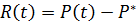. Решив с данным обозначением уравнение, полученное при вычитании . Получим решение данного уравнения:

Таким образом, получаем, что отклонение от равновесной цены изменяется по экспоненциальному закону. В зависимости от знака показателя степени может быть два качественно разных рынка: если знак положительный – асимптотическая устойчивость рынка, отрицательный – напротив, неустойчивость рынка.

Дискретизация непрерывной модели

Под дискретизацией системы подразумевается преобразование непрерывной динамической модели к дискретной форме описания в разностных уравнениях.

Математические модели дискретных систем устанавливают взаимосвязь между этими последовательностями.

Построение дискретного представления непрерывной системы носит название процесса дискретизации, или квантования, непрерывной системы. Пусть непрерывная система представлена своей внешней моделью:

А₀ y⁽ⁿ⁾(t) + А₁ y⁽ⁿ^-1)(t) + А₂ y⁽ⁿ^-2)(t) + … + А_n y(t) = u(t). (7)

При достаточно малом шаге квантования дискретизацию этой модели можно выполнить с необходимой точностью путем замены дифференциалов конечными разностями:

y'(t) = dy(t_k)/dt = Δy(t_k)/Δt = Δt^-1 (y(t_k₊₁) – y(t_k)),

y"(t) = d²y(t_k)/d²t = Δ²y(t_k)/Δ²t = Δt^-1 (Δy(t_k₊₁) – Δy(t_k)) = Δt^-2 (y(t_k₊₂) – 2y(t_k₊₁) + y(t_k)),

… и т.д.

После подстановки в (7) дискретная внешняя модель системы принимает конечно-разностный вид, который после алгебраических преобразований переводится в рекуррентную форму с постоянными коэффициентами модели a_i:

a₀ y(k+n) + a₁ y(k+n-1) + a₂ y(k+n-2) + … + a_n y(k) = u(k), (8)

В общем случае функция u(k) также может представлять собой полином:

a₀ y(k+n) + a₁ y(k+n-1) +…+ a_n y(k) = b₁ u(k+n-1) +…+ b_n u(k). (9)

Движение дискретной модели, представленной в разностном виде, складывается из двух движений: собственного и вынужденного под действием внешнего возмущения. Собственное движение - решение однородного разностного уравнения системы. Общий вид этого решения определяется как линейная форма от собственных чисел системы:

y(k) = C₁ λ₁^k + C₂ λ₂^k + … + C_n λ_n^k, (10)

где С_i - коэффициенты линейной формы, которые вычисляются через начальные состояния системы; λ_i - простые действительные корни характеристического уравнения системы:

a₀ λⁿ + a₁ λ^n-1 + a₂ λ^n-2 + … + a_n = 0. (11)

Операторная форма модели (10) может быть получена введением в рассмотрение оператора сдвига z:

zⁱ y(k) = y(k+i). (12)

При этом уравнение (12) легко преобразуется к виду

a(z) y(k) = b(z) u(k), (13)

a(z) = zⁿ + a₁z^n-1 +... + a_n-1z + a_n, (14)

b(z) = b₁z^n-1 +... + b_n-1z + b_n. (15)

Оператор a(z) называется характеристическим полиномом системы (14), а комплексные числа z_i, i = (1, n) - корни характеристического уравнения a(z)=0, называются полюсами системы. Корни алгебраического уравнения b(z) = 0 называются нулями системы.

Из выражения (15) следует операторное уравнение связи переменных y(k) и u(k) и оператор передаточной функции дискретной системы:

y(k) = W(z)u(k), (16)

W(z) = b(z)/a(z). (17)

Возмущающее воздействие f(k) влияния на объект управления внешней среды рассматривается как дополнительный входной сигнал, при этом линейная модель дискретной системы принимает вид:

a₀ y(k+n) + a₁ y(k+n-1) +…+ a_n y(k) =

a₀b₁ u(k+n-1) +…+ b_n u(k) + d₁ f(k+n-1) +…+ d_n f(k). (18)

где d_i - коэффициенты, определяющие влияние на процессы в системе возмущения f(k). После соответствующих преобразований получаем операторную форму модели:

a(z) y(k) = b(z) u(k) + d(z) f(k). (19)

d(z) = d₁zⁿ^-1 +... + d_n_-1z + d_n. (20)

y(k) = W(z)u(k) + W_f(z) f(k), (21)

W_f(z) = d(z)/a(z). (22)

W_f(z) - передаточная функция системы по возмущающему воздействию f(k).

Воспользуйтесь поиском по сайту: