 |
Дифференциальное уравнение теплопроводности.
|
|
|
|
Вариант16
Уравнение движения реальной жидкости.
Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения для идеальной жидкости
При движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной энергии.
Уравнение Бернулли для реальной жидкости будет иметь вид:
Из рисунка видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой).Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1-1 и 2-2.
Кроме этого в уравнении появились еще два коэффициента α1 и α2, которые называются коэффициентами Кориолиса и зависят от режима течения жидкости (α = 2 для ламинарного режима, α = 1 для турбулентного режима).
Потерянная высота h(1-2)пот складывается из линейных потерь, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока)
h(1-2) пот = hлин + hмест
С помощью уравнения Бернулли решается большинство задач практической гидравлики. Для этого выбирают два сечения по длине потока, таким образом, чтобы для одного из них были известны величины Р, ρ, g, а для другого сечения одна или величины подлежали определению. При двух неизвестных для второго сечения используют уравнение постоянства расхода жидкости υ1ω 1 = υ2ω2.
|
|
|
Дифференциальное уравнение теплопроводности.
Теория теплопроводности не рассматривает механизм процесса распространения теплоты, а ограничивается описанием этого процесса на основе закона сохранения энергии и закона Фурье.
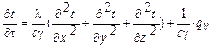
Дифференциальное уравнение Фурье отражает общий характер процесса, которое имеет множество решении. Для получения решения, соответствующего конкретной единичной задаче, необходимо задание условии однозначности. В условие однозначности входят геометрические условия, физические параметры материала, начальные условия и граничные условия. Условия однозначности содержат описание всех частных особенностей процесса, которые выделяют единичное явление из всего класса явлений теплопроводности.
Геометрические условия характеризуют форму и размер тела, в котором протекает процесс.
Физические условия определяют числовые значения всех физических параметров тела, входящих в дифференциальное уравнение теплопроводности и граничные условия, а также распределение внутренних источников теплоты qv.
Временные (начальные) условия характеризуют распределение температуры в теле в начальный момент времени и заключаются в том, что для начального момента времени τ0 должна быть известна функция t = f(x, y, z, τ0).
Граничные условия определяют особенности протекания процесса на границах тела и могут быть заданы следующим образом.
Граничные условия первого рода заключаются в том, что задается температура на поверхности тела.
Граничные условия второго рода заключаются в задании плотности теплового потока на поверхности тела.
Граничные условия третьего рода состоят в задании температуры окружающей среды и интенсивности теплообмена на поверхности тела. Эта интенсивность теплообмена оценивается коэффициентом теплоотдачи α.
|
|
|
Граничные условия четвертого рода характеризуются равенством тепловых потоков, проходящих через поверхность контакта двух тел.
|
|
|
