 |
Площадь надграфика (криволинейная трапеция ограничена отрицательной функцией и осью абсцисс)
|
|
|
|
Применение интеграла
Будем помнить то, что мы ограничены только определенным интегралом и остановимся на его применении. Для общего развития напомню, что интегральное исчисление не останавливается на интеграле первого рода в декартовых координатах, существуют кратные интегралы, криволинейные (1го и 2го рода), в полярных и сферических координатных плоскостях и т.д.
План:
1. Площадь криволинейной трапеции.
2. Объём тела вращения.
3. Длина дуги.
4. Площадь поверхности вращения.
5. Нахождение статического момента и центра тяжести кривой.
6. Нахождение статического момента и центра тяжести плоской фигуры.
7. Механическая работа.
I. Площадь криволинейной трапеции.
Площадь подграфика (криволинейная трапеция ограничена положительной функцией и осью абсцисс)
Пусть  (заданная непрерывная функция) и
(заданная непрерывная функция) и 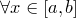
 (т.е. график функции находится только в верхней полуплоскости).
(т.е. график функции находится только в верхней полуплоскости).
Тогда площадь подграфика функции  равна
равна  .
.

 .
.
Пример 1:
Вычислить площадь подграфика функции  , на отрезке [0,2].
, на отрезке [0,2].
Чертим график, убеждаемся что он в верхней полуплоскости н данном промежутке, далее вычисляем интеграл:

Важно!!!! Нужно помнить, что площадь ни в коем случае не может оказаться отрицательной! Если получилось отрицательное значение, значит вы делали что-то не правильно!
Криволинейная трапеция ограничена двумя функциями
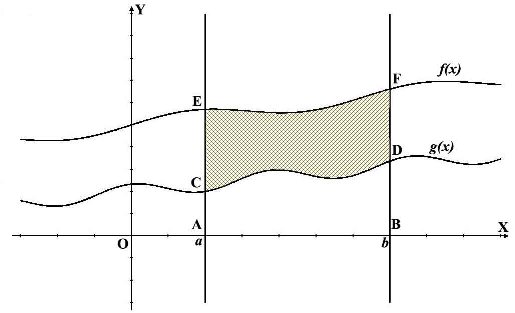
Во втором варианте наша фигура будет ограничена не осью абсцисс, а другой функцией g(x). Поэтому, что бы найти площадь CEFD, нам надо сначала найти площадь AEFB (с помощью интеграла от f(x)), потом найти площадь ACDB (с помощью интеграла от g(x)). И искомая площадь фигуры CEFD, будет разница между первой и второй площадями криволинейной трапеции. Поскольку границы интегрирования здесь одинаковые, то это всё можно записать под одним интегралом (смотрите формулы под рисунком) всё зависит от сложности функций, в каком случае проще будет найти интеграл.

|
|
|
Пример 2: Вычислить площадь криволинейной трапеции: функция  , функция
, функция  на отрезке [0,2].
на отрезке [0,2].
Чертим график, смотрим график какой из функций лежит выше, какой ниже: f(x)-выше, далее вычисляем интеграл:
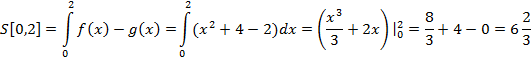
Пример 3: Вычислить площадь криволинейной трапеции: функция  , функция
, функция  на отрезке [0,2].
на отрезке [0,2].
Чертим график, смотрим график какой из функций лежит выше, какой ниже: g(x)-выше, далее вычисляем интеграл:

площадь надграфика (криволинейная трапеция ограничена отрицательной функцией и осью абсцисс)
Третий очень похож к первому, но только наша трапеция размещена, не над осью абсцисс, а под ней. Поэтому здесь надо брать такой же интеграл, только со знаком минус, потому что значение интеграла будет отрицательным, а значение площади должно быть положительное. Если вместо функции f(x) взять функцию –f(x), то её график будет такой же просто симметрически отображен относительно оси абсцисс.

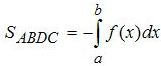
Пример 4:
Вычислить площадь надграфика функции 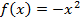 , на отрезке [0,2].
, на отрезке [0,2].
Чертим график, убеждаемся что он в нижней полуплоскости на данном промежутке, далее вычисляем интеграл:

4) Площадь фигуры ограниченной линиями.
Теперь рассмотрим более сложную конструкцию. На рисунке ниже мы видим четыре разных функции и плоскость, которую они образуют. Что бы найти её площадь нам надо рассмотреть каждую её часть, которая соответствует одной функции.
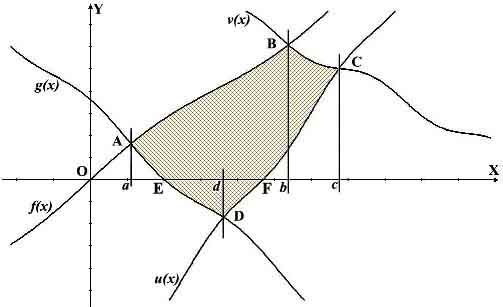
- Начнём с функции f(x) здесь нам надо искать интеграл от a до b, но при этом остаются небольшие уголки, площадь которых надо вычесть, что бы осталась только искомая площадь.
- Если взять функцию g(x), то видим, что она нам поможет найти площадь части фигуры, которая расположена под осью абсцисс, не забываем про знак минус для этой части интеграла. Также помним, что мы должны были вычесть один из уголков, который расположен под графиком этой функции. Поэтому у нас выходит интеграл со знаком минус от функции g(x) с границами от a до d.
- Следующей возьмём функцию v(x), видим, что здесь надо брать интеграл от b до c. Но видим, что наша фигура ограничивается не осью OX, а функцией u(x) поэтому надо ещё вычесть ту часть плоскости, которая попадает в этот интервал [b; c] и расположена между осью OX и графиком функции u(x).
- И последней рассмотрим функцию u(x), видим, что она нам поможет найти вторую часть фигуры, что расположена ниже оси абсцисс, а также помним, что мы должны вычесть ту часть площади, которая находится между осью OX и графиком функции u(x) до с. Поэтому, как и со второй функцией будем иметь интеграл со знаком минус, но теперь от функции u(x) и с границами от d до c.

|
|
|
Пример 5: Пусть имеем две функции:

И нам надо найти площадь фигуры ограниченной этими двумя функциями.
Преобразуем эти функции к следующему виду.

Нанесём их на декартовую систему координат и обозначим нашу фигуру:
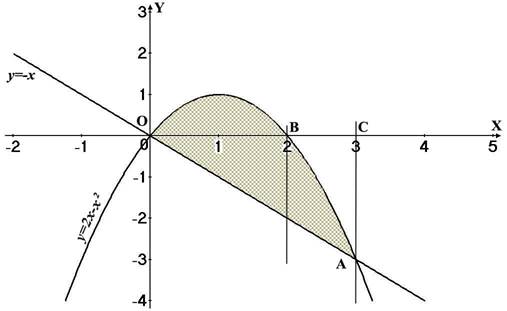
Находим самый правый и самый левый конец фигуры, это пересечения функций: точки 0 и 3. Значит это и будут пределы интегрирования. (Разбивать фигуру на части нет необходимости, т.к. нет больше пересечений и других крайних точек.)
Верхняя функция парабола, нижняя прямая. Пользуемся формулой из пункта 3)

Решив этот интеграл, мы и найдём площадь нужной нам фигуры.

II. Объем тела вращения

Пусть  , функция
, функция  непрерывна и
непрерывна и 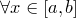
 . Рассмотрим тело, полученное вращением подграфика функции
. Рассмотрим тело, полученное вращением подграфика функции  вокруг оси абсцисс.
вокруг оси абсцисс.
Объем этого тела равен  .
.

III. Длина дуги
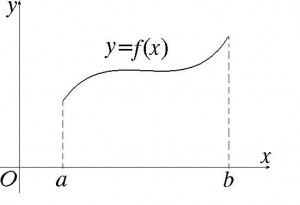
Пусть  , функция
, функция  дифференцируема, функция
дифференцируема, функция 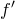 непрерывна. Нужно вычислить длину графика функции
непрерывна. Нужно вычислить длину графика функции  на отрезке
на отрезке  .
.
Тогда
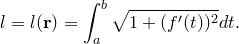
|
|
|


