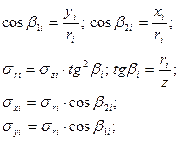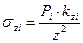 |
Определение напряжений в грунтах.
|
|
|
|
Определение напряжений в грунтах при действии местных нагрузок от фундаментов зданий и сооружений имеет большое практическое значение для определения деформаций и оценки условий прочности и устойчивости оснований. Напряжения распределяются в массиве грунта на значительную глубину и обеспечивают различные изменения в слоях грунта, составляющих основание. Оценка поведения несущей системы здания требует изучения напряженно-деформированного состояния на значительную глубину в примыкающих зонах грунтового массива.
В механике грунтов при решении вопросов о распределении напряжений применяют решения теории упругости, которые справедливы в пределах линейной зависимости изменения деформаций от приложенных нагрузок. Однако для определения общих деформаций грунтов с учетом одновременно протекающих как упругих, так и неупругих деформаций, решений теории упругости недостаточно. Здесь требуются добавочные условия, вытекающие из изучения физической природы грунтов как дисперсных тел и особенностей их деформирования под нагрузкой. При определении напряжений в грунтах, они рассматриваются как линейно деформируемые тела, у которых вся нагрузка передается на скелет грунта, а ее величина не превышает расчетной допустимой по условиям II-ой группы предельных состояний (
).
В практических условиях распределение нагрузок действующих на основание может быть различным для их учёта используются решение различных задач. Далее рассматриваются решение некоторых задач.
Действие сосредоточенной нагрузки на поверхности полупространства. Способ элементарного суммирования.
- Сосредоточенная нагрузка на поверхности грунта.
|
|
|
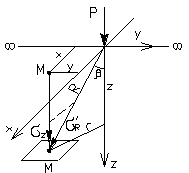Рис. 6.2. Схема напряжений на горизонтальной площадке
| 
|
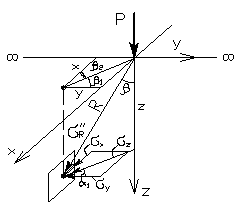Рис. 6.2. Схема напряжений на вертикальной площадке
| 
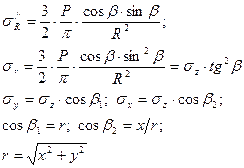Значения коэффициентов  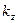приведены в таблице 6.1.
|
Таблица 6.1
|
|
|
|
|
|
|
|
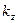
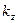
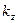
| 0,00 0,02 0,04 0,06 0,08 0,10 0,12 0,14 0,16 0,18 0,20 0,22 0,24 0,26 0,28 0,30 0,32 0,34 0,36 0,38 0,40 0,42 0,44 0,46 0,48 | 0,478 0,477 0,476 0,473 0,470 0,466 0,461 0,455 0,448 0,441 0,433 0,424 0,415 0,405 0,395 0,385 0,374 0,363 0,352 0,3408 0,329 0,318 0,307 0,296 0,284 | 0,50 0,52 0,54 0,56 0,58 0,60 0,62 0,64 0,66 0,68 0,70 0,72 0,74 0,76 0,78 0,80 0,82 0,84 0,86 0,88 0,90 0,92 0,94 0,96 0,98 | 0,273 0,262 0,252 0,241 0,231 0,221 0,212 0,202 0,193 0,185 0,176 0,168 0,160 0,153 0,146 0,139 0,132 0,126 0,120 0,114 0,108 0,103 0,098 0,093 0,089 | 1,00 1,02 1,04 1,06 1,08 1,10 1,12 1,14 1,16 1,18 1,20 1,22 1,24 1,26 1,28 1,30 1,32 1,34 1,36 1,38 1,40 1,42 1,44 1,46 1,48 | 0,084 0,080 0,076 0,073 0,069 0,066 0,063 0,060 0,057 0,054 0,051 0,049 0,047 0,44 0,042 0,040 0,038 0,036 0,035 0,033 0,032 0,030 0,029 0,028 0,026 | 1,50 1,52 1,54 1,56 1,58 1,60 1,62 1,64 1,66 1,68 1,70 1,74 1,78 1,82 1,86 1,90 1,94 1,98 2,00 2,20 2,40 2,60 2,80 3,00 4,00 | 0,025 0,024 0,023 0,022 0,021 0,020 0,019 0,018 0,018 0,017 0,016 0,015 0,014 0,012 0,011 0,011 0,010 0,009 0,008 0,006 0,004 0,003 0,002 0,002 0,000 |
Способ элементарного суммирования для определения напряжений.
Для сложных случаев загружения грунтовых оснований, когда строгое решение по распределению напряжений не получено, пользуются способом суммирования. Загрузочная площадь разбивается на площадки с размерами менее половины расстояния до рассматриваемых точек. Распределенная нагрузка на условно выделенных площадках приводится к сосредоточенной силе, которая приложена в их центрах тяжести. Напряжение в рассматриваемой точке определяется как сумма напряжений от сосредоточенных сил на условно выделенных площадках
|
|
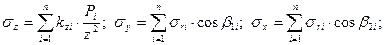
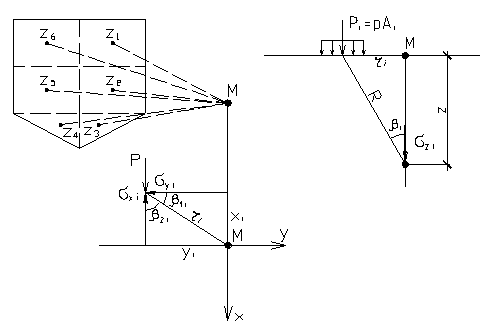
Рис.6.4. Схема к определению напряжений в массиве грунта по способу элементарного суммирования.
Распределение напряжений при равномерно распределенной нагрузке по площади прямоугольника. Метод угловых точек.
|
|
|
- Нагрузка по площади прямоугольника.
|
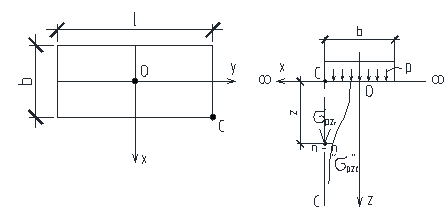
Решение для определения напряжений получено для точек, лежащих на вертикали, проходящих через угловую точку прямоугольника.
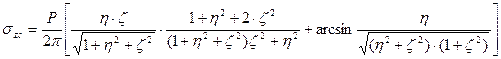
Для практических расчетов принимается табличный метод:
;
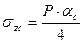Величины 
приведены в таблице 6.2.
Таблица 6.2
Коэффициент (α) распределения напряжений (σpz) по глубине основания под центром подошвы столбчатых и ленточных фундаментов (ζ о=2z/b), под углом столбчатого и под краем ленточного фундаментов (ζ c=z/b).
| ζ о=2z/b ζ c=z/b | Для фундаментов с соотношением сторон η=l/b | |||||||
| 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 | 2,4 | |
| 0,0 0,2 0,4 0,6 0,8 1,0 | 1,0000 0,9944 0,9604 0,8916 0,7996 0,7008 | 1,0000 0,9956 0,9680 0,9100 0,8300 0,7404 | 1,0000 0,9960 0,9716 0,9200 0,8480 0,7644 | 1,0000 0,9964 0,9736 0,9260 0,8588 0,7820 | 1,0000 0,9964 0,9748 0,9296 0,8660 0,7924 | 1,0000 0,9964 0,9756 0,9316 0,8704 0,7996 | 1,0000 0,9968 0,9760 0,9332 0,8732 0,8048 | 1,0000 0,9968 0,9764 0,9340 0,8752 0,8080 |
| 1,2 1,4 1,6 1,8 2,0 | 0,6064 0,5232 0,4492 0,3876 0,3360 | 0,6504 0,5692 0,4964 0,4332 0,3788 | 0,6820 0,6032 0,5316 0,4688 0,4136 | 0,7032 0,6276 0,5584 0,4964 0,4412 | 0,7172 0,6452 0,5780 0,5176 0,4632 | 0,7272 0,6576 0,5928 0,5336 0,4808 | 0,7372 0,6668 0,6036 0,5460 0,4940 | 0,7396 0,6740 0,6120 0,5556 0,5052 |
| 2,2 2,4 2,6 2,8 3,0 | 0,2926 0,2568 0,2264 0,2008 0,1788 | 0,3328 0,2936 0,2604 0,2320 0,2076 | 0,3668 0,3252 0,2900 0,2596 0,2332 | 0,3936 0,3516 0,3152 0,2836 0,2560 | 0,4156 0,3736 0,3363 0,3044 0,2760 | 0,4336 0,3916 0,3548 0,3220 0,2928 | 0,4480 0,4064 0,3696 0,3368 0,3076 | 0,4596 0,4188 0,3820 0,3500 0,3204 |
| 3,2 3,4 3,6 3,8 4,0 | 0,1604 0,1444 0,1304 0,1184 0,1080 | 0,1868 0,1684 0,1528 0,1392 0,1272 | 0,2104 0,1908 0,1732 0,1580 0,1448 | 0,2320 0,2108 0,1920 0,1756 0,1512 | 0,2508 0,2284 0,2092 0,1916 0,1764 | 0,2672 0,2444 0,2244 0,2064 0,1896 | 0,2816 0,2584 0,2376 0,2192 0,2028 | 0,2940 0,2708 0,2496 0,2308 |
| 4,2 4,4 4,6 4,8 5,0 | 0,0988 0,0908 0,0836 0,0772 0,0716 | 0,1164 0,1072 0,0988 0,0916 0,0848 | 0,1332 0,1224 0,1132 0,1048 0,0972 | 0,1484 0,1372 0,1268 0,1176 0,1096 | 0,1628 0,1504 0,1392 0,1296 0,1208 | 0,1756 0,1628 0,1512 0,1408 0,1312 | 0,1876 0,1744 0,1620 0,1512 0,1412 | 0,1984 0,1848 0,1720 0,1608 0,1504 |
| 6,0 7,0 8,0 9,0 10,0 11,0 12,0 | 0,0508 0,0376 0,0292 0,0232 0,0188 0,0156 0,0131 | 0,0604 0,0448 0,0348 0,0276 0,0224 0,0186 0,0157 | 0,0696 0,0520 0,0404 0,0320 0,0260 0,0217 0,0183 | 0,0784 0,0588 0,0456 0,0364 0,0296 0,0248 0,0209 | 0,0872 0,0656 0,0508 0,0408 0,0332 0,0278 0,0234 | 0,0952 0,0720 0,0560 0,0448 0,0368 0,0308 0,0260 | 0,1028 0,0780 0,0612 0,0488 0,0400 0,0337 0,0285 | 0,1104 0,0840 0,0660 0,0528 0,0436 0,0367 0,0310 |
| ζ о=2z/b ζ c=z/b | Для фундаментов с соотношением сторон η=l/b | |||||||
| 2,4 | 2,6 | 2,8 | 3,0 | 3,2 | 3,4 | 3,6 | 3,8 | |
| 0,0 0,2 0,4 0,6 0,8 1,0 | 1,0000 0,9968 0,9764 0,9340 0,8752 0,8080 | 1,0000 0,9968 0,9768 0,9348 0,8768 0,8104 | 1,0000 0,9968 0,9768 0,9352 0,8776 0,8124 | 1,0000 0,9968 0,9768 0,9356 0,8784 0,8136 | 1,0000 0,9968 0,9772 0,9360 0,8792 0,8148 | 1,0000 0,9968 0,9772 0,9360 0,8796 0,8156 | 1,0000 0,9968 0,9772 0,9364 0,8796 0,8160 | 1,0000 0,9968 0,9772 0,9364 0,8800 0,8164 |
| 1,2 1,4 1,6 1,8 2,0 | 0,7396 0,6740 0,6120 0,5556 0,5052 | 0,7432 0,6784 0,6180 0,5632 0,4992 | 0,7460 0,6820 0,6228 0,5692 0,5200 | 0,7480 0,6848 0,6268 0,5736 0,5256 | 0,7492 0,6872 0,6296 0,5772 0,5296 | 0,7504 0,6888 0,6320 0,5800 0,5328 | 0,7512 0,6900 0,6336 0,5820 0,5356 | 0,7520 0,6912 0,6348 0,5840 0,5380 |
| 2,2 2,4 2,6 2,8 3,0 | 0,4596 0,4188 0,3820 0,3500 0,3204 | 0,4688 0,4284 0,3924 0,3600 0,3312 | 0,4764 0,4368 0,4012 0,3692 0,3404 | 0,4820 0,4432 0,4080 0,3768 0,3480 | 0,4872 0,4488 0,4140 0,3828 0,3548 | 0,4908 0,4532 0,4188 0,3880 0,3604 | 0,4940 0,4568 0,4232 0,3928 0,3652 | 0,4968 0,4600 0,4264 0,3964 0,3692 |
| 3,2 3,4 3,6 3,8 4,0 | 0,2940 0,2708 0,2496 0,2308 0,2140 | 0,3048 0,2816 0,2604 0,2412 0,2240 | 0,3144 0,2908 0,2696 0,2504 0,2352 | 0,3224 0,2988 0,2776 0,2584 0,2412 | 0,3292 0,3060 0,2848 0,2656 0,2480 | 0,3352 0,3120 0,2912 0,2720 0,2544 | 0,4200 0,3172 0,2964 0,2776 0,2600 | 0,3444 0,3216 0,3012 0,2824 0,2655 |
| 4,2 4,4 4,6 4,8 5,0 | 0,1984 0,1848 0,1720 0,1608 0,1504 | 0,2084 0,1940 0,1812 0,1696 0,1588 | 0,2172 0,2018 0,1896 0,1776 0,1668 | 0,2252 0,2108 0,1972 0,1852 0,1740 | 0,2324 0,2176 0,2040 0,1920 0,1804 | 0,2384 0,2240 0,2104 0,1980 0,1864 | 0,2440 0,2296 0,2160 0,2036 0,1920 | 0,2492 0,2344 0,2212 0,2088 0,1972 |
| 6,0 7,0 8,0 9,0 10,0 11,0 12,0 | 0,1104 0,0840 0,0660 0,0528 0,0436 0,0367 0,0310 | 0,1172 0,0896 0,0704 0,0568 0,0468 0,0396 0,0334 | 0,1240 0,0953 0,0748 0,0608 0,0500 0,0424 0,0359 | 0,1300 0,1004 0,0792 0,0644 0,0528 0,0453 0,0383 | 0,1360 0,1052 0,0836 0,0676 0,0560 0,0481 0,0407 | 0,1412 0,1100 0,0876 0,0712 0,0588 0,0508 0,0430 | 0,1464 0,1184 0,0912 0,0744 0,0616 0,0535 0.0454 | 0,1508 0,1184 0,0948 0,0776 0,0648 0,0562 0,0477 |
|
|
|
| ζ о=2z/b ζ c=z/b | Для фундаментов с соотношением сторон η=l/b | Ленточ-ный η≥10 | ||||||
| 3,8 | 4,0 | 5,0 | 6,0 | 7,0 | 8,0 | 9,0 | ||
| 0,0 0,2 0,4 0,6 0,8 1,0 | 1,0000 0,9968 0,9772 0,9364 0,8800 0,8164 | 1,0000 0,9968 0,9772 0,9364 0,8800 0,8168 | 1,0000 0,9968 0,9772 0,9368 0,8808 0,8176 | 1,0000 0,9968 0,9772 0,9368 0,8808 0,8180 | 1,0000 0,9968 0,9772 0,9368 0,8808 0,8180 | 1,0000 0,9968 0,9772 0,9368 0,8808 0,8184 | 1,0000 0,9968 0,9772 0,9368 0,8808 0,8184 | 1,0000 0,9968 0,9773 0,9368 0,8810 0,8184 |
| 1,2 1,4 1,6 1,8 2,0 | 0,7520 0,6912 0,6348 0,5840 0,5380 | 0,7528 0,6920 0,6360 0,5858 0,5400 | 0,7540 0,6940 0,6392 0,5896 0,5452 | 0,7548 0,6952 0,6404 0,5912 0,5472 | 0,7552 0,6956 0,6404 0,5920 0,5484 | 0,7552 0,6956 0,6412 0,5924 0,5488 | 0,7552 0,6956 0,6416 0,5928 0,5492 | 0,7554 0,6960 0,6417 0,5931 0,5498 |
| 2,2 2,4 2,6 2,8 3,0 | 0,4968 0,4600 0,4264 0,3964 0,3992 | 0,4992 0,4624 0,4292 0,3996 0,3724 | 0,5056 0,4700 0,4380 0,4096 0,3836 | 0,5084 0,4736 0,4424 0,4144 0,3892 | 0,5096 0,4752 0,4444 0,4164 0,3920 | 0,5104 0,4760 0,4452 0,4180 0,3932 | 0,5108 0,4764 0,4460 0,4188 0,3944 | 0,5114 0,4774 0,4471 0,4200 0,3956 |
| 3,2 3,4 3,6 3,8 4,0 | 0,3444 0,3216 0,3012 0,2824 0,2655 | 0,3480 0,3256 0,3052 0,2868 0,2696 | 0,3600 0,3388 0,3196 0,3012 0,2848 | 0,3664 0,3456 0,3264 0,3092 0,2932 | 0,3692 0,3492 0,3304 0,3136 0,2980 | 0,3712 0,3508 0,3328 0,3160 0,3008 | 0,3720 0,3520 0,3340 0,3175 0,3024 | 0,3741 0,3544 0,3367 0,3205 0,3058 |
| 4,2 4,4 4,6 4,8 5,0 | 0,2492 0,2344 0,2212 0,2088 0,1972 | 0,2536 0,2388 0,2256 0,2132 0,2016 | 0,2696 0,2556 0,2424 0,2304 0,2188 | 0,2784 0,2648 0,2520 0,2404 0,2292 | 0,2836 0,2704 0,2576 0,2464 0,2356 | 0,2864 0,2736 0,2616 0,2504 0,2396 | 0,2884 0,2756 0,2636 0,2524 0,2424 | 0,2922 0,2798 0,2684 0,2579 0,2481 |
| 6,0 7,0 8,0 9,0 10,0 11,0 12,0 | 0,1508 0,1184 0,0948 0,0776 0,0648 0,0562 0.0477 | 0,1552 0,1224 0,0984 0,0808 0,0668 0,0588 0,0500 | 0,1724 0,1384 0,1132 0,0940 0,0792 0,0714 0,0608 | 0,1840 0,1504 0,1244 0,1040 0,0888 0,0828 0,0709 | 0,1916 0,1584 0,1328 0,1128 0,0968 0,0932 0,0801 | 0,1964 0,1644 0,1392 0,1192 0,1032 0,1026 0,0885 | 0,2000 0,1684 0,1436 0,1240 0,1080 0,1112 0,0963 | 0,2084 0,1795 0,1575 0,1403 0,1265 0,1152 0,1056 |
|
|
|
Метод угловых точек.
Для определения напряжений σz на осях, не проходящих через угол прямоугольника загружения, применяется метод достраивания прямоугольников через заданную ось и площадь загрузки.
Случай 1, вертикальная ось проходит через центр подошвы фундамента. Через точку О проводятся линии параллельно сторонам подошвы,
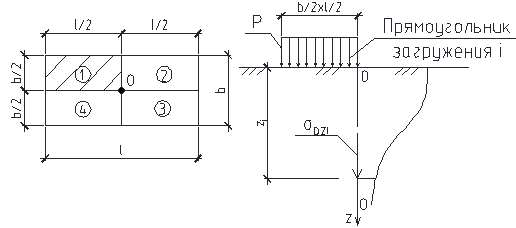
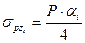
прямоугольник со сторонами 
разбивается на 4-е одинаковых прямоугольника со сторонами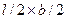 
, для которых точка О является угловой. Напряжение в любой точке по глубине на оси О-О определяется как сумма напряжений под углами 4-х равных прямоугольников
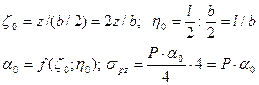
Величины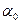 
принять по таблице 6.2.
Случай 2, вертикальная ось О-О расположена внутри прямоугольника и не проходит через его центр. Через точку проводятся линии параллельные сторонам подошвы, прямоугольник условно разделяется на 4-е прямоугольника со сторонами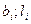 
, для которых точка О является угловой.
| Напряжения по оси О-О на любой глубине z под подошвой прямоугольника определится как сумма напряжений под углами 4-х прямоугольников:
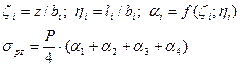Величины  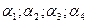принять по таблице 6.2.
|
Случай 3, когда вертикальная ось О-О расположена за пределами контура прямоугольника загружения. Через точку О и подошву прямоугольника загружения строится прямоугольники, для которых она будет угловой. Напряжения по оси на глубину z ниже подошвы фундамента определяется как сумма напряжений под углами всех условных прямоугольников. Напряжения от загружающих прямоугольников принимаются со знаком плюс «+», а от разгружающих со знаком минус «-».
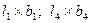| Загружающие прямоугольники:  . Разгружающие прямоугольники:  . Суммарное влияние нагрузки определяется прямоугольником
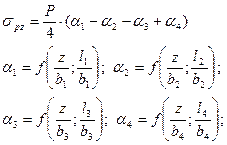Величины 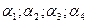принять по таблице 6.2.
|
|
|
|
|
|
|
