Проблема выбора решения в условиях неопределенности

В предыдущем параграфе мы рассмотрели обратную задачу исследования операций в детерминированном случае, когда показатель эффективности W зависит только от двух групп факторов: заданных, заранее известных а и элементов решения х. Реальные задачи исследования операций чаще всего содержат помимо этих двух групп еще одну — неизвестные факторы, которые в совокупности мы обозначим одной буквой ξ. Итак, показатель эффективности W зависит от всех трех групп факторов:

 

W=W(a, х, ξ). (5.1)

Так как величина W зависит от неизвестных факторов ξ то даже при заданных и х она уже не может быть вычислена, остается неопределенной. Задача поиска оптимального решения тоже теряет определенность. Ведь не можем же мы максимизировать неизвестную величину W! И все-таки нас не покидает желание сделать эту неизвестную величину по возможности максимальной. Ведь добиваются же успеха люди в условиях, когда не вся обстановка ясна? Иногда добиваются. Переводя сказанное на математический язык, поставим перед собой следующую задачу.

При заданных условиях , с учетом неизвестных факторов ξ, найти такое решение х 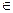X, которое, по возможности, обеспечивает максимальное значение показателя эффективности W.

Это уже другая, не чисто математическая задача (недаром в ее формулировке сделана оговорка «по возможности»). Наличие неопределенных факторов ξ переводит задачу в новое качество: она превращается в задачу о выборе решения в условиях неопределенности.

Порассуждаем немного о возникшей задаче. Прежде всего, будем честны: неопределенность есть неопределенность, и ничего хорошего в ней нет. Если условия операции неизвестны, мы не можем так же успешно оптимизировать решение, как мы это сделали бы, если бы располагали большей информацией. Поэтому любое решение, принятое в условиях неопределенности, хуже решения, принятого в заранее известных условиях. Что делать? Плохое или хорошее — решение все равно должно быть принято. Наше дело — придать этому решению в возможно большей мере черты разумности. Недаром Т. Л. Саати, один из видных зарубежных специалистов по исследованию операций, определяя свой предмет, говорит не без иронии: «Исследование операций представляет собой искусство давать плохие ответы на практические вопросы, на которые даются еще худшие ответы другими методами».

Задача принятия решения в условиях неопределенности на каждом шагу встречается нам в жизни. Например, мы собрались путешествовать, и укладываем в чемодан вещи. Размеры и вес чемодана, а также имеющийся у нас набор вещей заданы (условия ), погода в районе путешествия заранее неизвестна (условия ξ). Какие предметы одежды (х) надо взять с собой? Эта задача, внешне сходная с задачами исследования операций, конечно, решается нами без всякой математики (незачем «стрелять из пушек по воробьям»), но все же не без опоры на некоторые статистические данные, скажем, о вероятной погоде в районе путешествия, а также собственной склонности к простудам; нечто вроде оптимизации решения, сознательно или бессознательно, мы производим. Любопытно, что разные люди при этом, по-видимому, пользуются разными показателями эффективности. Если молодой человек, скорее всего, стремится максимизировать сумму приятных впечатлений (оставим в стороне вопрос о том, как ее оценить количественно), то пожилой путешественник, пожалуй, предпочтет минимизировать вероятность заболевания...

Теперь возьмем более серьезную задачу. Планируется ассортимент товаров для распродажи на ярмарке. Желательно было бы максимизировать прибыль. Однако заранее неизвестно ни количество покупателей, которые придут на ярмарку, ни потребности каждого из них. Как быть? Неопределенность налицо, а принимать решение нужно!

Другой пример: проектируется система сооружений, оберегающих район от паводков. Ни моменты их наступления, ни размеры заранее неизвестны. А проектировать все-таки нужно, и никакая неопределенность не избавит нас от этой обязанности...

Наконец, еще более сложная задача: разрабатывается план развития вооружения на несколько лет вперед. Неизвестны ни конкретный противник, ни вооружение, которым он будет располагать. А решение принимать надо!

Для того чтобы такие решения принимать не наобум, по вдохновению, а трезво, с открытыми глазами, современная наука располагает рядом приемов. Каким из них воспользоваться — зависит от того, какова природа неизвестных факторов ξ, откуда они возникают и кем контролируются. Другими словами, с какого вида неопределенностью мы в данной задаче сталкиваемся?

Прежде всего, рассмотрим наиболее благоприятный для исследования, так сказать, «доброкачественный» вид неопределенности. Это случай, когда неизвестные факторы ξ представляют собой обычные объекты изучения теории вероятностей — случайные величины (или случайные функции), статистические характеристики которых нам известны или в принципе могут быть получены к нужному сроку. Такие задачи исследования операций мы будем называть стохастическими задачами, а присущую им неопределенность — стохастической неопределенностью.

Приведем пример стохастической задачи исследования операций. Пусть организуется или реорганизуется работа столовой с целью повысить ее пропускную способность. Нам в точности неизвестно, какое количество посетителей придет в нее за рабочий день, когда именно они будут появляться, какие блюда заказывать и сколько времени будет продолжаться обслуживание каждого из них. Однако характеристики этих случайных величин, если сейчас еще не находятся в нашем распоряжении, могут быть получены статистическим путем.

Другой пример: организуется система профилактического и аварийного ремонта технических устройств с целью уменьшить простои техники за счет неисправностей и ремонтов. Отказы техники, длительности ремонтов и профилактик носят случайный характер. Характеристики всех случайных факторов, входящих в задачу, могут быть получены, если собрать соответствующую статистику.

Рассмотрим более подробно этот «доброкачественный» вид неопределенности. Пусть неизвестные факторы ξ представляют собой случайные величины с какими-то, в принципе известными, вероятностными характеристиками — законами распределения, математическими ожиданиями, дисперсиями и т. п. Тогда показатель эффективности W, зависящий от этих факторов, тоже будет величиной случайной. Максимизировать случайную величину невозможно: при любом решении х она остается случайной, неконтролируемой. Как же быть?

Первое, что приходит в голову: а нельзя ли заменить случайные факторы ξ их средними значениями (математическими ожиданиями)? Тогда задача становится детерминированной и может быть решена обычными методами.

Что и говорить — прием соблазнительный и в некоторых случаях даже оправданный. Ведь на практике, решая большинство задач физики, механики, техники, мы сплошь и рядом им пользуемся, пренебрегая случайностью ряда параметров (теплоемкость, индуктивность, коэффициент трения) и заменяя их средними значениями. Весь вопрос в том, насколько случайны эти параметры: если они мало отклоняются от своих математических ожиданий, так поступать можно и нужно. Так же обстоит дело и в исследовании операций: есть задачи, в которых случайностью можно пренебречь. Например, если мы составляем план снабжения группы предприятий сырьем, можно в первом приближении пренебречь, скажем, случайностью фактической производительности источников сырья (если, разумеется, его производство хорошо налажено). Тот же прием — пренебречь случайностью и заменить все входящие в задачу случайные величины их математическими ожиданиями — будет уже опрометчивым, если влияние случайности па интересующий нас исход операции существенно. Возьмем самый грубый пример: пусть мы ведем обстрел какой-то цели, стремясь, во что бы то пи стало попасть в нее. Производится несколько выстрелов. Давайте, заменим все случайные координаты точек попадания их математическим ожиданием — центром цели. Получится, что любой выстрел с гарантией попадет в цель, что заведомо неверно. Другой, менее очевидный, пример: планируется работа ремонтной мастерской, обслуживающей автобазу. Пренебрежем случайностью момента появления неисправности (т. е. заменим случайное время безотказной работы машины его математическим ожиданием) и случайностью времени выполнения ремонта. И что же окажется? Мастерская, работа которой спланирована без учета случайности, попросту не будет справляться со своей задачей. Встречаются операции, в которые случайность входит по существу, и свести задачу к детерминированной не удается.

Итак, рассмотрим такую операцию Ơ, где факторы ξ «существенно случайны» и заметно влияют на показатель эффективности W, который тоже «существенно случаен».

Возникает мысль: надо взять в качестве показателя эффективности среднее значение (математическое ожидание) этой случайной величины W = M [ W ] и выбрать такое решение х, при котором этот усредненный по условиям показатель обращается в максимум:

 

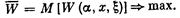(5.2)

 

Заметим, что именно так мы поступали в § 2, выбирая в качестве показателя эффективности в задачах, содержащих неопределенность, не просто «доход», а «средний доход», не просто «время», а «среднее время». В большинстве случаев такой подход (мы его назовем «оптимизацией в среднем») вполне оправдан. В самом деле, если мы выберем решение так, чтобы среднее значение показателя эффективности обращалось в максимум, то, безусловно, поступим правильнее, чем, если бы выбирали решение наобум.

А как же с элементом неопределенности? Конечно, в какой-то мере он сохраняется. Эффективность каждой отдельной операции, проводимой при конкретных значениях случайных факторов ξ, может сильно отличаться от ожидаемой как в большую, так, к сожалению, и в меньшую сторону. Нас может утешить то, что, оптимизируя операцию «в среднем», мы, в конечном счете, после многих ее повторений выиграем больше, чем, если бы совсем не пользовались расчетом.

Такая «оптимизация в среднем» очень часто применяется на практике в стохастических задачах исследования операций, и пользуются ею обычно не задумываясь над ее правомочностью. А задуматься надо! Чтобы этот прием был законным, нужно, чтобы операция обладала свойством повторяемости, и «недостача» показателя эффективности в одном случае компенсировалась его «избытком» в другом. Например, если мы предпринимаем длинный ряд однородных операций с целью получить максимальный доход, то доходы от отдельных операций суммируются, «минус» в одном случае покрывается «плюсом» в другом, и все в порядке.

Всегда ли это будет так? Нет, не всегда! Чтобы убедиться в этом, рассмотрим пример. Организуется автоматизированная система управления (АСУ) для службы неотложной медицинской помощи большого города. Вызовы, возникающие в разных районах города в случайные моменты, поступают на центральный пункт управления, откуда они передаются на тот или другой пункт неотложной помощи с приданными ему машинами. Требуется разработать такое правило (алгоритм) диспетчерской работы АСУ, при котором служба в целом будет функционировать наиболее эффективно. Для этого, прежде всего, надо выбрать показатель эффективности W.

Разумеется, желательно, чтобы время Т ожидания врача было минимально. Но это время — величина случайная. Если применить «оптимизацию в среднем», то надо выбрать тот алгоритм, при котором среднее время ожидания минимально. Не так ли?

Оказывается, не совсем так! Беда в том, что времена ожидания врача отдельными больными не суммируются: слишком долгое ожидание одного из них не компенсируется почти мгновенным обслуживанием другого. Выбирая в качестве показателя эффективности среднее время ожидания Т, мы рискуем дать предпочтение тому алгоритму, при котором среднее-то время ожидания мало, но отдельные больные могут ожидать врача очень долго! Чтобы избежать таких неприятностей, можно дополнить показатель эффективности добавочным требованием, чтобы фактическое время Т ожидания врача было не больше какого-то предельного значения t₀. Поскольку Т — величина случайная, нельзя просто потребовать, чтобы выполнялось условие Т 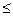t₀; можно только потребовать, чтобы оно выполнялось с очень большой вероятностью, настолько большой, чтобы событие Т 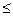t₀; было практически достоверным. Ну что же, назначим какое-то значение 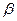, близкое к единице (например, 0,99 или 0,995), настолько близкое, что событие с такой вероятностью можно считать практически достоверным, и потребуем, чтобы условие Т 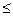t₀ выполнялось с вероятностью, не меньшей, чем :

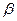Р (Т 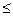t₀) 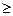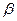. (5.3)

Введение такого ограничения означает, что из области возможных решений Х исключаются решения, ему не удовлетворяющие. Ограничения типа (5.3) называются стохастическими ограничениями; наличие таких ограничений сильно усложняет задачу оптимизации.

Особенно осторожным надо быть с «оптимизацией в среднем», когда речь идет не о повторяемой, массовой операции, а о единичной, «уникальной». Все зависит от того, к каким последствиям может привести неудача данной операции, т. е. слишком малое значение показателя эффективности W; иногда оно может означать попросту катастрофу. Что толку в том, что операция в среднем приносит большой выигрыш, если в данном, единичном случае она может нас дотла разорить? От таких катастрофических результатов можно опять-таки спасаться введением стохастических ограничений. При достаточно большом значении уровня доверия 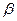можно быть практически уверенным в том, что угрожающее разорение нас не постигнет.

Итак, мы вкратце рассмотрели случай «доброкачественной» (стохастической) неопределенности и в общих чертах осветили вопрос об оптимизации решения в таких задачах. Но это, как говорится, цветочки, ягодки будут впереди! Стохастическая неопределенность — это почти определенность, если только известны вероятностные характеристики входящих в задачу случайных факторов. Гораздо хуже обстоит дело, когда неизвестные факторы ξ не могут быть изучены и описаны статистическими методами. Это бывает в двух случаях: либо а) распределение вероятностей для параметров 1 в принципе существует, но к моменту принятия решения не может быть получено, либо б) распределение вероятностей для параметров ξ вообще не существует.

Пример ситуации типа а): проектируется информационно-вычислительная система (ИВС), предназначенная для обслуживания каких-то случайных потоков требований (запросов). Вероятностные характеристики этих потоков требований в принципе могли бы быть получены из статистики, если бы данная ИВС (или аналогичная ей) уже существовала и функционировала достаточно долгое время. Но к моменту создания проекта такой информации нет, а решение принимать надо! Как быть?

Разумеется, можно заранее (из умозрительных соображений) задаться какими-то характеристиками случайных факторов ξ оптимизировать решение х на этой основе (просто «в среднем» или при стохастических ограничениях) и остановиться па нем. Это будет, безусловно, лучше, чем выбрать решение наобум, но не намного лучше. Гораздо разумнее будет применить следующий прием: оставить некоторые элементы решения х свободными, изменяемыми. Затем выбрать для начала какой-то вариант решения, зная заведомо, что он не самый лучший, и пустить систему в ход, а потом, по мере накопления опыта, целенаправленно изменять свободные параметры решения, добиваясь того, чтобы эффективность не уменьшалась, а увеличивалась. Такие совершенствующиеся в процессе применения алгоритмы управления называются адаптивными. Преимущество адаптивных алгоритмов в том, что они не только избавляют пас от предварительного сбора статистики, по н перестраиваются в ответ па изменение обстановки. По мере накопления опыта такой алгоритм постепенно улучшается, подобно тому, как живой человек «учится па ошибках».

Теперь обратимся к самому трудному и неприятному случаю б), когда у неопределенных факторов ξ вообще не существует вероятностных характеристик; другими словами, когда их нельзя считать «случайными» в обычном смысле слова.

Поясняем: под термином «случайное явление» в теории вероятностей принято понимать явление, относящееся к классу повторяемых и, главное, обладающее свойством статистической устойчивости. При повторении однородных опытов, исход которых случаен, их средние характеристики проявляют тенденцию к устойчивости, стабилизируются. Частоты событий приближаются к их вероятностям, средние арифметические — к математическим ожиданиям. Если много раз бросать монету, частота появления герба постепенно стабилизируется, перестает быть случайной; если много раз взвешивать па аналитических весах одно и то же тело, средний результат перестает колебаться, выравнивается. Это пример доброкачественной, стохастической неопределенности.

Однако бывает неопределенность и нестохастнческого вида, которую мы условно назовем «дурной неопределенностью». Несмотря на то, что факторы t заранее неизвестны, не имеет смысла говорить об их «законах распределения» или других вероятностных характеристиках.

Пример: допустим, планируется некая торгово-промышленная операция, успех которой зависит от того, юбки какой длины ξ будут носить женщины через два года. Распределение вероятностей для величины ξ в принципе не может быть получено ни из каких статистических данных. Даже если рассмотреть великое множество опытов (годов), начиная с тех отдаленных времен, когда женщины впервые надели юбки, и в каждом из них зарегистрировать величину ξ, это вряд ли поможет нам в нашем прогнозе. Вероятностное распределение величины ξ попросту не существует, так как не существует массива однородных опытов, где она обладала бы должной устойчивостью. Налицо случай «дурной неопределенности».

Как же все-таки быть в таких случаях? Отказаться вообще от применения математических методов и выбрать решение «волевым» образом? Нет, этого делать не стоит. Некоторую пользу предварительные расчеты могут принести даже в. таких скверных условиях.

Давайте поразмышляем на эту тему. Пусть выбирается решение х в какой-то операции Ơ, условия которой содержат «дурную неопределенность» — параметры ξ, относительно которых никаких сведений мы не имеем, а можем делать лишь предположения. Попробуем все же решить задачу.

Первое, что приходит в голову: а ну-ка, зададимся какими-то, более или менее правдоподобными, значениями параметров ξ. Тогда задача перейдет в категорию детерминированных и может быть решена обычными методами (детерминированный случай, со всеми его трудностями, представляется нам теперь чуть ли не «курортом»!).

Нет, радоваться рано. Допустим, что, затратив много усилий и времени (своего и машинного), мы это сделали. Ну и что? Будет ли найденное решение хорошим для других условий ξ. Как правило, нет. Поэтому ценность его — сугубо ограниченная. В данном случае разумно будет выбрать не решение х, оптимальное для каких-то условий ξ, а некое компромиссное решение, которое, не будучи оптимальным, может быть, ни для каких условий, будет все же приемлемым в целом их диапазоне.

В настоящее время полноценной научной теории компромисса не существует, хотя некоторые попытки в этом направлении в теории игр и статистических решений делаются. Обычно окончательный выбор компромиссного решения осуществляется человеком. Опираясь па предварительные расчеты, в ходе которых решается большое число прямых задач исследования операций для разных условий ξ и разных вариантов решения х, он может оценить сильные и слабые стороны каждого варианта и на этой основе сделать выбор. Для этого необязательно знать точный «условный» оптимум для каждой совокупности условий ξ. Математические вариационные методы в данном случае отступают на задний план.

Подчеркнем еще одну полезную функцию предварительных математических расчетов в задачах с «дурной неопределенностью»: они помогают заранее отбросить те решения х 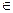X, которые при любых условиях ξ уступают другим, т. е. оказываются неконкурентоспособными. В ряде случаев это помогает существенно сузить множество X, иногда — свести его к небольшому числу вариантов, которые легко могут быть просмотрены и оценены человеком в поисках удачного компромисса.

При рассмотрении задач исследования операций с «дурной неопределенностью» всегда полезно сталкивать в споре разные подходы, разные точки зрения. Среди последних надо отметить одну, часто применяемую в силу своей математической определенности, которую можно назвать «позицией крайнего пессимизма». Она сводится к тому, что, принимая решение в условиях «дурной неопределенности», надо всегда рассчитывать на худшее и принимать то решение, которое дает максимальный эффект в наихудших условиях. Если в этих условиях мы получаем выигрыш W = 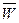, то можно гарантировать, что в любых других он будет не меньше («принцип гарантированного результата»). Этот подход привлекателен тем, что дает четкую постановку задачи оптимизации и возможность ее решения корректными математическими методами. Но он оправдан далеко не всегда. Область его применения — по преимуществу так называемые «конфликтные ситуации», в которых условия зависят от сознательно действующего лица («разумного противника»), отвечающего на любое наше решение наихудшим для нас образом. В более нейтральных ситуациях принцип «гарантированного выигрыша» не является единственно возможным, но может быть рассмотрен наряду с другими. Пользуясь им, нельзя забывать, что эта точка зрения — крайняя, что на ее основе можно выбрать только очень осторожное, «перестраховочное» решение, которое не всегда будет разумным. Вообразите себе, например, военачальника, который всякое свое решение будет принимать исходя из гипотезы, что его противник необычайно умей, хитер и изворотлив и на каждое его действие немедленно ответит наихудшим для него образом. Вряд ли такому военачальнику будет сопутствовать удача! Напротив, в любой конкретной ситуации нужно стараться угадать, в чем слаб и «глуп» противник, и стараться «обвести его вокруг пальца». Тем менее уместен крайне пессимистический подход в ситуациях, где стороне, принимающей решение, не противостоят никакие враждебные силы. Расчеты, основанные на точке зрения «крайнего пессимизма», всегда должны корректироваться разумной долей оптимизма. Вряд ли стоит становиться и на противоположную точку зрения — крайнего пли «залихватского» оптимизма, но известная доля риска при принятии решения все же должна присутствовать. Нельзя также забывать о том, что любое решение, принятое в условиях «дурной неопределенности»,— неизбежно плохое решение, и вряд ли стоит обосновывать его с помощью тонких и кропотливых расчетов. Скорее следует подумать о том, откуда можно было бы взять недостающую информацию. Здесь все способы хороши — лишь бы прояснить положение.

Упомянем в этой связи об одном довольно оригинальном методе, не пользующемся любовью в среде чистых математиков, но тем не менее полезном, а иногда — единственно возможном. Речь идет о так называемом методе экспертных оценок. Он часто применяется в задачах, связанных с прогнозированием в условиях дурной неопределенности (например, в футурологии). Грубо говоря, идея метода сводится к следующему: собирается коллектив сведущих, компетентных в данной области людей, и каждому из них предлагается ответить на какой-то вопрос (например, назвать срок, когда будет совершено то или другое открытие, пли оценить вероятность того или другого события). Затем полученные ответы обрабатываются наподобие статистического материала. Результаты обработки, разумеется, сохраняют субъективный характер, но в гораздо меньшей степени, чем, если бы мнение высказывал один эксперт («ум хорошо, а два — лучше»). Подобного рода экспертные оценки для неизвестных условий могут быть применены и при решении задач исследования операций с дурной неопределенностью. Каждый из экспертов па глаз оценивает степень правдоподобия различных вариантов условий 1, приписывая им какие-то субъективные вероятности. Несмотря на субъективный характер оценок каждого эксперта, усредняя оценки целого коллектива, можно получить нечто более объективное и полезное (кстати, оценки разных экспертов расходятся не так сильно, как можно было бы ожидать). Таким образом, задача с дурной неопределенностью как бы сводится к обычной стохастической задаче. Разумеется, к полученным отсюда выводам не надо относиться слишком доверчиво, но наряду с другими результатами, вытекающими из других точек зрения, но все же могут помочь при выборе решения.

Наконец, сделаем одно общее замечание. При обосновании решения в условиях неопределенности, что бы мы ни делали, элемент неопределенности, «гадательности» сохраняется. Поэтому нельзя предъявлять к точности решений слишком высокие требования. Вместо того чтобы указать одно-единственное, в точности «оптимальное» (с какой-то точки зрения) решение, лучше выделить целую область «приемлемых» решений, которые оказываются несущественно хуже других, какой бы точкой зрения мы ни пользовались. В пределах этой области и должны производить свой окончательный выбор ответственные за это люди. Исследователь, предлагая им рекомендации по выбору решения, всегда должен одновременно указывать точки зрения, из которых вытекают те или другие рекомендации.

 

⇐ Предыдущая1234

Поделиться:

Воспользуйтесь поиском по сайту: