Исследование функции с помощью производной.

Практическая работа №10

 

по дисциплине: Математика

 

наименование работы: Применение производной к исследованию функций и построению графиков

 

 

Для специальностей: 210705, 210709, 210723, 210111, 230115

Работа рассчитана на 2 часа

 

 

Смоленск, 2013

1. Цель работы: усвоить применение производной функции для исследования функции на монотонность, экстремумы, точки перегиба и выпуклость графика с целью построения графика.

 

2. Литература:

2.1. Дадаян, А.А. Математика:учебник./А.А. Дадаян.-3-е изд.-М.:ФОРУМ, 2011.-544с.- ISBN 978-5-9134-460-3

2.2. Дадаян, А.А. Сборник задач по математике: учебное пособие/А.А. Дадаян.-М.:ФОРУМ:ИНФРА-М,2011.-352 с.-ISBN 978-5-91134-271-5, ISBN 978-5-16-002152-2 2.3. Антонов,В.И. Элементарная математика для первокурсника: Учебное пособие. / В.И Антонов, Ф.И. Копелевич.- СПб.: Издательство "Лань", 2013. -112с.: ил. -ISBN 978-5-8114-1413-0

 

3. Подготовка к работе:

3.1. Повторить тему «Применение производной к исследованию функций и построению графиков».

3.2. Подготовить бланк отчета (см.п.7).

3.3. Ответить на вопросы допуска:

3.3.1. Что такое производная функции в точке?

3.3.2. Запишите таблицу производных элементарных функций?

3.3.3. Какие правила дифференцирование вы знаете?

 

4. Основное оборудование:

4.1. не используется.

5. Задание:

Выполните задание согласно варианту.

Вариант 1

1. Исследуйте функцию и постройте ее график:

.

Вариант 2

1. Исследуйте функцию и постройте ее график:

.

Вариант 3

1. Исследуйте функцию и постройте ее график:

.

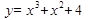Вариант 4

1. Исследуйте функцию и постройте ее график:

.

Вариант 5

1. Исследуйте функцию и постройте ее график:

.

6. Порядок выполнения работы:

6.1. Ознакомиться с заданием.

6.2. Определить номер варианта (в соответствии с номером в журнале).

6.3. Выполнить задания в соответствии с вариантом.

6.4. Ответьте на контрольные вопросы.

 

7. Содержание отчёта:

7.1. Название и цель работы.

7.2. Указать номер варианта, привести условия задач своего варианта.

7.3. Представить решение задач согласно варианта.

7.4. Ответы на контрольные вопросы.

 

8. Контрольные вопросы:

8.1. Какую точку называют критической точкой функции?

8.2. Дайте определение точки максимума функции?

8.3. Дайте определение точки минимума функции?

8.4. Когда график функция возрастает на промежутке?

8.5. Когда график функция убывает на промежутки?

8.6. В чем заключается понятие выпуклости и вогнутости графика функции?

8.7. Какая точка называется точкой перегиба?

 

Составил преподаватель __________________________Скряго О.С.

9. Приложение:

ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНОЙ.

Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками функции.

 

Функция возрастает (убывает) на промежутке, если на данном промежутке производная больше нуля (меньше нуля).

Если критическая точка принадлежит D(f), а производная в данной точке меняет свой знак с плюса на минус (с минуса на плюс), то это точка максимума (точка минимума).

Пусть функция дважды дифференцируема на некотором интервале. Тогда:

– если вторая производная на интервале, то график функции является выпуклым на данном интервале;

– если вторая производная на интервале, то график функции является вогнутым на данном интервале.

Если вторая производнаяпри переходе через точкуменяет знак, то в данной точке существует перегиб графика функции.

Пример: Исследовать функцию и построить ее график.

Решение:

1) Область определения функции.

2) Четность, нечетность.

Функция общего вида.

3) Точки пересечения с осями.

а) с осью :

то есть точки

б) с осью 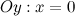: в данной точке функция неопределенна.

4) Асимптоты.

а) вертикальные: прямые и 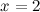- вертикальные асимптоты.

б) горизонтальные асимптоты:

то есть прямая 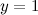- горизонтальная асимптота.

в) наклонные асимптоты :

Таким образом, наклонных асимптот нет.

5) Критические точки функции, интервалы возрастания, убывания.

Найдем точки, в которых первая производная равна нулю или не существует: для любого из области определения функции; не существует при и .

Таким образом, функция убывает на всей области существования.Точек экстремума нет.

6) Точки перегиба, интервалы выпуклости, вогнутости.

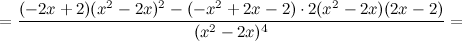
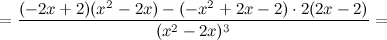
Найдем точки, в которых вторая производная равна нулю или не существует: ; при и 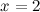вторая производная не существует.

Таким образом, на промежутках и 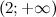функция вогнута, а на промежутках и - выпукла. Так как при переходе через точку 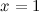вторая производная поменяла знак, то эта точка является точкой перегиба.

7) Эскиз графика.

Поделиться:

Воспользуйтесь поиском по сайту: