Представление колебательных процессов типовых форм.

Практическое занятие № 4

 

Тема: Реализация алгоритмов воспроизведения испытательных сигналов с заданными характеристиками

Цель работы: приобретение практических умений в воспроизведении сигналов с заданными характеристиками (детерминированных и случайных).

 

Основные теоретические сведения

Очевидно, что поведение динамических систем (ДС) как в статике, так и в динамике существенным образом зависит от того, каким образом изменяются во времени внешние воздействия, приложенные к системе. Здесь возникает трудность принципиального характера, которая заключается в том, что реальные законы изменения внешних воздействий заранее, как правило, неизвестны, т. е. представляют собой случайные функции времени. Чтобы обойти эту трудность, при исследовании ДС часто ориентируются на так называемые типовые законы изменения внешних воздействий, в качестве которых принимают либо наиболее вероятные, либо наиболее неблагоприятные законы изменения задающего и возмущающего воздействий.

Сигналы и помехи действующие в системах разделяют на такие группы:

· детерминированные сигналы;

· случайные сигналы.

В реальных системах чаще всего действуют одновременно и детерминированные, и случайные воздействия. В таких случаях говорят, что система находите; под влиянием стохастических сигналов.

Детерминированные сигналы - это сигналы, параметры и мгновенные значения которых могут быть определены в любой момент времени (периодические и непериодические).

Случайные сигналы не являются заранее известными функциями времени, и их можно описать лишь с помощью вероятностных характеристик: математического ожидания (среднего значения), дисперсии, корреляционной функции и спектральной плотности. Для определения характеристик случайного сигнала в системе, необходимо произвести ряд экспериментов, в результате чего формируется выборка сигнала. Результат каждого эксперимента по регистрации исследуемого сигнала называется выборочной функцией (реализацией), а совокупность таких реализаций — случайным процессом.

Случайные процессы разделяют на стационарные (эргодические и неэргодические) и нестационарные.

В программе MATLAB предусмотрены процедуры, обеспечивающие формирование тестовых последовательностей данных:

Представление одиночных импульсных процессов типовых форм.

· Формирование одиночного импульса прямоугольной формы. Обращение вида:

y = rectpuls (t,w),

позволяет образовать вектор у значений сигнала такого импульса единичной амплитуды, шириной w, центрированного относительно t = 0 по заданному вектору t моментов времени. Если ширина импульса w не указана, ее значение по умолчанию принимается равным единице.

Пример:

t = 0:0.01:10;

y = 0.75*rectpuls (t-3,2) + 0.5*rectpuls(t-8,0.4)+1.35*rectpuls(t-5,0.8);

plot(t,y),grid

title('Одиночные импульсы прямоугольной формы')

xlable('Время (с)')

ylable('Выходной процесс Y(t)')

· Формирование импульса треугольной формы единичной амплитуды. Обращение вида:

y = tripuls (t,w,s),

аргументы y, t, w имеют тот же смысл. Аргумент s (-1<s<1) определяет наклон треугольника. Если s = 0 или не указан, треугольный импульс имеет симметричную форму.

Пример:

t = 0:0.01:10;

y = 0.75*tripuls (t-1,0.5) + 0.5*tripuls(t-5,0.5,-1)+1.35*tripuls(t-3,0.8,1);

plot(t,y),grid

title('Единичные импульсы треугольной формы')

xlable('Время (с)')

ylable('Выходной процесс Y(t)')

Представление колебательных процессов типовых форм.

· формирование колебаний в виде последовательности импульсов. Обращение вида:

y = pulstran (t,d,'func',p1,p2,…)

здесь d определяет вектор значений тех моментов времени, где должны быть центры соответствующих импульсов; параметр func определяет форму импульсов и может быть одно из значений: rectpuls, tripuls; параметры p1,p2, … определяют необходимые параметры импульса в соответствии с формой обращения к процедуре, определяющей этот импульс.

Пример:

t = 0:0.01:50;

d = [0:50/5:50]';

y = 0.75*pulstran(t,d,'func',5);

plot(t,y),grid

title('Последовательность импульсов _________ формы')

xlable('Время (с)')

ylable('Выходной процесс Y(t)')

3. Формирование случайных процессов с заданной спектральной плотностью выполняется путем пропускания случайного процесса, белого шума (идеализированный случайный сигнал, у которого спектральная плотность постоянна на всех частотах от 0 до ¥, а корреляционная функция равна d-функции) через некоторое динамическое звено – формирующий фильтр.

Формирующий фильтр (ФФ) — устройство, позволяющее генерировать случайный сигнал с заданной спектральной плотностью из сигнала белого шума. Характеристики формирующего фильтра для стационарных случайных сигналов определяются, следующим образом. Так как спектральная плотность сигнала является четной дробно-рациональной функцией частоты, то. она может быть представлена в виде двух комплексно-сопряженных сомножителей: 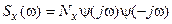, откуда и находится передаточная функция формирующего фильтрата

.

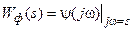Для расчета коэффициентов передаточной функции формирующего фильтра выражение для спектральной плотности сигнала нужно записать в виде

.

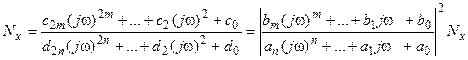Вычислив квадрат модуля в левой части и приравняв коэффициенты при одинаковых степенях частоты слева и справа, получим уравнения для определения коэффициентов передаточной функции формирующего фильтрата 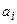и .

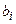На практике выражение для передаточной функции формирующего фильтра удобнее находить путем применения процедуры винеровской факторизации для заданной спектральной плотности (СП). Обращение имеет вид:

[bf,af]=sfp(b,a);

W = tf(bf,af)

где входные переменные: b - вектор-столбец коэффициентов полинома числителя исходной функции СП; a - вектор-столбец коэффициентов полинома знаменателя исходной функции СП; выходные переменные: bf - вектор-столбец коэффициентов полинома числителя передаточной функции ФФ, где все нули и полюса расположены в левой полуплоскости; af - вектор-столбец коэффициентов полинома знаменателя этой передаточной функции ФФ.

Пакет SIMULINK позволяет осуществлять исследование (моделирование) поведения динамических систем. Ввод характеристик исследуемых систем производится в диалоговом режиме, путем графической сборки схемы соединений элементарных стандартных звеньев. В результате такой сборки образуется модель исследуемой системы, которую в дальнейшем будем называть S-моделью. Модель хранится в файле с расширением.mdl.

В пакете SIMULINK белый шум моделируется с помощью блока, который находится в библиотеке модулей, раздел Sources, изображенного на рис.1

рис.1

Пропустив белый шум через быстрый преобразователь Фурье, работающего с короткими реализациями (Short Time FFT – Estimation - DSP Blockset -) можно увидеть единичную спектральную плотность процесса на осциллографе (Scope). Для того, чтобы получить допустимую точность спектрального анализа надо иметь реализацию с такой длиной, которая бы в несколько раз превышала время корреляции процесса. Поскольку это время для белого шума очень маленькое, то точность оценки будет достаточная. Сигнал на выходе определенного формирующего фильтра W(s) имеет очень большое время корреляции, а потому его невозможно оценить таким преобразователем.

Чтобы обработать результаты моделирования в MATLABе необходимо на схеме в пакете SIMULINK достроить так называемую рабочую область (to workspase), в которой данные записываются в виде многомерного массива с переменным числом строк, причем элементы первого столбца содержат последовательность значений модельного времени.

Средства программы MATLAB позволяют определять некоторые статистические характеристики случайного процесса, в частности, спектральную плотность мощности при помощи функции psd, без указания выходных величин выводит график зависимости спектральной плотности от частоты.

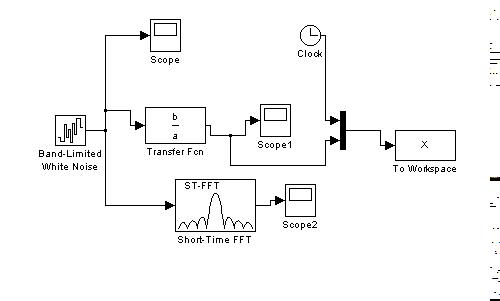
Рис.2

Ход работы:

1) Сформировать тестовую последовательность одиночных импульсов с заданными параметрами.

2) Сформировать колебания в виде последовательности импульсов заданной формы.

3) Определить ПФ ФФ для формирования случайного сигнала с заданной спектральной плотностью. По примеру заданной схемы (рис.2) собрать необходимую модель в пакете SIMULINK.

4) Построить спектральную плотность мощности сформированного случайного сигнала, представить ее в логарифмическом масштабе.

Варианты заданий:

1. а)На интервале времениt = 0:0.1:20 два одиночных импульса прямоугольной формы: амплитудой 10 и 3.7; центрированные: 1-й на 5 момент времени, 2-й на 15 момент времени; шириной: 1-й - 4, 2-й – 1.

б) Сформировать колебания в виде последовательности треугольных импульсов на интервале времени t = 0:0.01:100, центрирование в моменты времени 100/10, шириной 4, с наклоном s=0.5.

в) .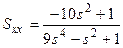

2. а)На интервале времениt = 0:0.01:10 два одиночных импульса треугольной формы: амплитудой – 2, 6; центрированные: 1-й на 1 момент времени, 2-й на 5 момент времени; шириной: 1-й – 0.5, 2-й – 0.8, с наклоном s=0.5.

б) Сформировать колебания в виде последовательности прямоугольных импульсов на интервале времени t = 0:0.01:50, центрирование в моменты времени 50/5, шириной 3.

в) .

3. а) На интервале времениt = 0:0.1:20 четыре одиночных импульса прямоугольной формы: амплитудой – 1, 2, 3, 4; центрированные: 1-й на 2 момент времени, 2-й на 5 момент времени, 3-й на 9 момент времени, 4-й на 15 момент времени, все шириной 1.

б) Сформировать колебания в виде последовательности треугольных импульсов на интервале времени t = 0:0.01:70, центрирование в моменты времени 70/7, шириной 3.5, с наклоном s=-0.5.

в) .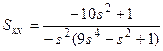

4. а)На интервале времениt = 0:0.01:10 три одиночных импульса треугольной формы: амплитудой – 2, 3.8, 4; центрированные: 1-й на 2 момент времени, 2-й на 5 момент времени, 3-й на 9 момент времени, все шириной 1, все с наклоном s=0.25.

б) Сформировать колебания в виде последовательности прямоугольных импульсов на интервале времени t = 0:0.01:80, центрирование в моменты времени 80/8, шириной 4.5.

в) .

5. а) На интервале времениt = 0:0.01:10 три одиночных импульса прямоугольной формы: амплитудой – 10, 3, 5; центрированные: 1-й на 3 момент времени, 2-й на 5 момент времени, 3-й на 9 момент времени, все шириной 1.

б) Сформировать колебания в виде последовательности треугольных импульсов на интервале времени t = 0:0.01:100, центрирование в моменты времени 100/5, шириной 10, с наклоном s=0.25.

в) .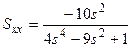

6. а) На интервале времениt = 0:0.1:20 четыре одиночных импульса треугольной формы: амплитудой – 4, 3, 2, 1; центрированные: 1-й на 2 момент времени, 2-й на 5 момент времени, 3-й на 9 момент времени, 4-й на 15 момент времени, все шириной 1.5, с наклоном s= - 0.5.

б) Сформировать колебания в виде последовательности прямоугольных импульсов на интервале времени t = 0:0.01:50, центрирование в моменты времени 50/5, шириной 2.

в) .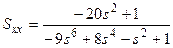

7. а) На интервале времениt = 0:0.01:10 два одиночных импульса прямоугольной формы: амплитудой – 10, 1.5; центрированные: 1-й на 3 момент времени, 2-й на 7 момент времени; шириной 3 и 1.5.

б) Сформировать колебания в виде последовательности треугольных импульсов на интервале времени t = 0:0.01:90, центрирование в моменты времени 90/9, шириной 2, с наклоном s= - 0.25.

в) .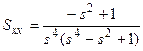

8. а)На интервале времениt = 0:0.01:10 три одиночных импульса треугольной формы: амплитудой – 2, 3.8, 4; центрированные: 1-й на 2 момент времени, 2-й на 5 момент времени, 3-й на 9 момент времени, все шириной 1, все с наклоном s=0.25.

б) Сформировать колебания в виде последовательности прямоугольных импульсов на интервале времени t = 0:0.01:80, центрирование в моменты времени 80/8, шириной 4.5.

в) .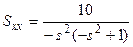

9. а)На интервале времениt = 0:0.01:10 два одиночных импульса треугольной формы: амплитудой – 2, 6; центрированные: 1-й на 1 момент времени, 2-й на 5 момент времени; шириной: 1-й – 0.5, 2-й – 0.8, с наклоном s=0.5.

б) Сформировать колебания в виде последовательности прямоугольных импульсов на интервале времени t = 0:0.01:50, центрирование в моменты времени 50/5, шириной 3.

в) .

10. а) На интервале времениt = 0:0.01:10 три одиночных импульса прямоугольной формы: амплитудой – 10, 3, 5; центрированные: 1-й на 3 момент времени, 2-й на 5 момент времени, 3-й на 9 момент времени, все шириной 1.

б) Сформировать колебания в виде последовательности треугольных импульсов на интервале времени t = 0:0.01:100, центрирование в моменты времени 100/5, шириной 10, с наклоном s=0.25.

в) .

 

Контрольные вопросы

1. Что такое детерминированный сигнал? Приведете примеры.

2. Что такое случайный сигнал?

3. Каковы основные характеристики случайных сигналов?

4. Почему при исследовании свойств динамических систем используют тесовые сигналы, изменяющиеся по определенному типовому закону?

5. Что такое стохастический сигнал?

6. Что такое стационарный эргодический сигнал?

7. С помощью какой функции программы MATLAB задаются одиночные импульсы прямоугольной формы?

8. С помощью какой функции программы MATLAB задаются одиночные импульсы треугольной формы?

9. Как сформировать колебательный процесс из импульсов заданной формы?

10. Что такое белый шум, каковы его основные характеристики?

11. Что такое формирующий фильтр? Как определить его передаточную функцию?

12. Что такое факторизация? С помощью какого оператора выполняется процедура винеровской полиномиальной факторизации?

13. Какой блок пакета SIMULINK позволяет обработать результаты моделирования в MATLABе?

14. Что такое спектральная плотность?

 

Поделиться:

Воспользуйтесь поиском по сайту: