 |
Геометрические характеристики плоских фигур
|
|
|
|
Утверждено редакционно-издательским советом ВоГТУ
Составители: Шапкина В.А., доцент
Комиссарова И.И., доцент
Рецензент: Михалевич Н.В., доцент
Введение
В брошюру включены задачи расчетно-проектировочных работ по курсу «Сопротивление материалов с основами строительной механики», краткие методические указания к выполнению РПР, отдельные справочные данные, вопросы к защите РПР.
Перечень расчетно-проектировочных работ охватывает основные разделы курса, по которым специалист должен иметь необходимые знания и умения: геометрические характеристики поперечного сечения; растяжение или сжатие стержней (статически определимых и статически неопределимых); прямой плоский изгиб балок, внецентренное сжатие, статически определимые рамы и фермы.
Каждый студент выполняет индивидуальное задание в соответствии с номером варианта.
При выполнении расчетно-проектировочных работ рекомендуется следующее:
- предварительно изучить соответствующий теоретический материал курса;
- записать условие задания с численными значениями параметров;
- начертить расчетную схему с указанием на чертеже числовых значений нагрузок и размеров;
- выполнить необходимые расчеты в десятичных дробях, оставляя три значащие цифры;
- рисунки и расчеты выполнять на отдельных листах формата А4 (210*297мм);
- эпюры внутренних усилий, напряжений, перемещений строить на одном листе под расчетной схемой; на эпюрах указывать числовые значения соответствующих ординат и единицы их измерения, знаки проставлять внутри эпюры.
Защита расчетно-проектировочных работ состоит в ответах на контрольные вопросы и в умении решать задачи по их тематике.
|
|
|
Примечание. Основные положения теории, относящиеся к данной теме курса, находятся, прежде всего, в конспектах лекций. Полное изложение всех разделов содержится в учебниках [1] и [3], а примеры решения задач в учебном пособии [2]. Успехов!
Растяжение и сжатие стержней
Задача 1А. Центральное растяжение и сжатие статически определимого ступенчатого стержня (рис. 1.1)
Ступенчатый стержень находится под действием продольных расчетных сил. Материал стержня – сталь. Исходные данные приведены в табл.1.1.
Требуется:
1. Построить эпюру продольных сил.
2. Построить эпюру нормальных напряжений по длине бруса.
3. Проверить прочность бруса.
4. Построить эпюру перемещений сечений бруса.
Примечания: – точки приложения сил располагаются либо на границах участков, либо в середине участка,
– модуль упругости материала (сталь) Е=2·105 МПа,
– расчетное сопротивление стали на растяжение
R =210 МПа.
Исходные данные к задачам 1А и 1Б
Таблица 1.1
| № груп пы | Длина участка, м | Площадь поперечного сечения, см2 | Нагрузка, кН | |||||||||
| l1 | l2 | l3 | A1 | A2 | A3 | F1 | F2 | F3 | F4 | F5 | F6 | |
| 0,6 | 0,5 | 0,7 | ||||||||||
| 0,4 | 0,7 | 0,5 | ||||||||||
| 0,8 | 0,6 | 0,3 |
Литература: [1, § 3.8 (пример 5), 8.9, 9.8], [2, § 71-73], [3, гл.11]
Схемы к работе 1А

Рис.1.1

Рис.1.1

Рис.1.1
Задача 1Б. Центральное растяжение и сжатие статически неопределимого ступенчатого стержня (рис.1.2)
Ступенчатый стержень нагружен продольными расчетными силами. Материал стержня – сталь, зазор Δ=0.1 мм. Исходные данные приведены в таблице 1.1.
Требуется:
1. Построить эпюру продольных сил.
2. Построить эпюру нормальных напряжений по длине бруса.
3. Проверить прочность бруса.
4. Построить эпюру перемещений сечений бруса.
Примечания: – точки приложения сил располагаются либо на границах участков, либо в середине участка,
|
|
|
– модуль упругости материала (сталь) Е=2·105 МПа,
– расчетное сопротивление стали на растяжение
R=210 МПа.
Схемы к работе 1Б

Рис.1.2


Рис.1.2


Рис.1.2
Контрольные вопросы к защите задач 1А и 1Б
1. Что такое внутренние силы? Порядок их определения методом сечений.
2. Какой вид сопротивления называют центральным растяжением-сжатием?
3. Что такое продольная сила в сечении? Правило её знаков.
4. Что такое напряжение в точке? Формула нормальных напряжений при растяжении-сжатии.
5. Какое напряжение считают опасным (предельным) для пластичных материалов?
6. Какие напряжения считают опасными для хрупкого материала?
7. Допускаемое напряжение для пластичного материала при растяжении и при сжатии.
8. Допускаемые напряжения для хрупкого материала при растяжении и при сжатии.
9. Условие прочности при растяжении-сжатии бруса из пластичного материала.
10. Условия прочности при растяжении-сжатии бруса из хрупкого материала.
11. Какие задачи решаются на основании условия прочности при растяжении-сжатии?
12. Закон Гука при растяжении-сжатии.
13. Закон Пуассона. Возможные значения коэффициента Пуассона.
14. Абсолютная и относительная деформации. Связь между ними. Как они вычисляются?
15. Что такое перемещение сечения бруса при растяжении-сжатии?
Геометрические характеристики плоских фигур
Задача 2А. Определение геометрических характеристик несимметричного сечения.Исходные данные взять в табл.2.1, рис 2.1.
Требуется:
1. Вычислить значения главных центральных моментов инерции
2. Определить значения моментов сопротивления
Исходные данные Таблица 2.1
| № группы | размеры | номер | ||||
| листа, см | уголка, мм | Двутавра | Швеллера | |||
| h | b | равнобокого | неравнобокого | |||
| 2.0 | 80х80х8 | 100х63х7 | ||||
| 1.8 | 125х125х10 | 110х70х8 | ||||
| 1.8 | 90х90х7 | 125х80х10 | 24а |
Примечание: поскольку сечение включает в себя прокатные профили, то следует воспользоваться таблицами сортамента стального проката, из которых выписать все нужные данные и начертить сечение в масштабе 1:1 или 1:2, или 1:4.
Литература: [1, § 3.8 (пример 5), 8.9, 9.8], [2, § 71-73], [3, гл.11]
Для решения данной задачи используем краткий алгоритм ее решения
|
|
|
1. Найти положение центра тяжести сечения.
Далее необходимо выбрать самому расчетчику две произвольные оси х/ и у/ и вычислить статические моменты сечения относительно каждой из этих осей:
 ,
,  .
.
Наконец, вычислить координаты центра тяжести:
 ,
,  , где А=∑Аi .
, где А=∑Аi .
2. Вычислить осевые и центробежный моменты инерции относительно случайных центральных осей «х» и «у», пользуясь при этом данными сортамента, формулами для прямоугольника (для стального листа) и формулами перехода при параллельном переносе осей:
 ,
,
 ,
,
 ,
,
где: xi и yi – собственные центральные оси каждой отдельной фигуры, из которых состоит заданное сечение;
аi – расстояние между осями «xi» и центральной осью всего сечения «х»;
вi – расстояние между осями «yi» и центральной осью всего сечения «y»;
Эти расстояния определяются в системе общих случайных центральных осей х и у, следовательно, могут быть как положительными, так и отрицательными.
3. Найти положение главных центральных осей (xо и yо):
 .
.
Показать на чертеже главные центральные оси «xо» и «yо», учитывая, что положительный угол αо соответствует повороту против часовой стрелки, а отрицательный – по часовой стрелке.
4. Определить величины главных центральных моментов инерции:
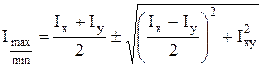 ,
,
Чтобы установить, какая из двух главных центральных осей максимальная, а какая из них минимальная, достаточно оценить по чертежу, какая ось хо и уо оказывается ближе к более «тяжелой» случайной центральной оси. Она и является осью с максимальным моментом инерции.
5. Выполненные выше расчеты верны, если их результаты удовлетворяют следующим двум проверкам:
а) 
б)  .
.
6. Определить значения моментов сопротивления
Схемы к работе 2А

Рис.2.1


Рис.2.1

Рис.2.1
Задача 2Б. Определение геометрических характеристик симметричного сечения, состоящего из простых геометрических фигур. Исходные данные взять в табл.2.2, рис 2.2.
Требуется:
1. Найти положение центра тяжести.
2. Показать главные центральные оси.
3. Вычислить главные центральные моменты инерции и осевые моменты сопротивления.
|
|
|
Таблица 2.2
| № группы | Размеры сечения, см | |
| а | в | |
Схемы к работе 2Б

Рис.2.2

Рис.2.2
Контрольные вопросы к защите задач 2А и 2Б
1. Статический момент, моменты инерции, момент сопротивления: их определения, размерности, знаки.
2. Чему равен статический момент сечения относительно центральной оси?
3. В каких случаях и какие геометрические характеристики обращаются в нуль?
4. Какие моменты инерции всегда положительны?
5. Как определить координаты центра тяжести сложного сечения?
6. Приведите формулы моментов инерции и моментов сопротивления для простых сечений (прямоугольник, круг, треугольник).
7. Как изменяется центробежный момент инерции при повороте осей на 90˚?
8. Какие оси называются главными центральными? Какими свойствами они обладают?
9. В каких случаях можно без вычислений установить положение главных осей?
10. Почему ось симметрии является всегда одной из главных центральных осей инерции?
11. В чем состоит закон суммы осевых моментов инерции?
12. Как вычисляется момент сопротивления сечения?
13. Как вычисляется радиус инерции?
|
|
|


