Главная | Обратная связь | Поможем написать вашу работу!

Сложное сопротивление

РАЗДЕЛ 3. СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ

Растяжение - сжатие

Задача 1. Для стального стержня круглого поперечного сечения, находящегося под действием распределённой нагрузки и осевых сил
(рис. 3.1), необходимо:

1. определить величины продольных сил на каждом участке стержня
и построить эпюру ;

2. по условию прочности выявить опасный участок стержня
и определить площади каждого участка;

3. определить величины нормальных напряжений на всех участках стержня и построить эпюру s;

4. определить величины перемещений для каждой характерной точки стержня и построить эпюры .

Дано:

1. , , ;

2. , , ;

3. допускаемое напряжение ;

4. модуль упругости

Рис. 3.1. Схема стержня

Решение. 1. Для определения продольных сил , разбиваем стержень на определённые участки и делаем сечения начиная с не закреплённого конца стержня (рис. 3.5).

Рассмотрим первый участок I-I (рис. 3.2). Его длина изменяется от 0 до ().

Действие стержня на отсечённый участок заменяем продольной силой , величина которой определится по следующему уравнению:

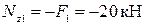Данное уравнение показывает, что на всём первом участке стержня внутренняя продольная сила имеет постоянное значение. Знак минус указывает, что первый участок испытывает сжатие.

Рис. 3.2. Первый отсечённый участок

Рассмотрим второй участок II - II (рис. 3.3). Его длина изменяется
от 0 до ().

Рис. 3.3. Второй отсечённый участок

Действие стержня на отсечённый участок заменяем продольной силой , величина которой численно равна алгебраической сумме проекций всех сил, действующих на отсечённую часть стержня:

(1)

Уравнение (1) имеет переменную в первой степени, следовательно, графиком данного уравнения является наклонная прямая. Определим величины на границах второго участка:

- ;

- .

Рассмотрим третий участок III - III (рис. 3.4). Его длина изменяется от 0 до (). Действие стержня на отсечённый участок заменяем продольной силой , величина которой определится по уравнению:

Данное уравнение показывает, что на всём протяжении третьего участка внутренняя продольная сила имеет постоянное значение.

Рис. 3.4. Третий отсечённый участок

По полученным данным строим эпюру , предварительно выбрав масштабный коэффициент (рис. 3.5).

2. Для определения опасного участка стержня и величин площадей каждого участка, запишем условие прочности при растяжении-сжатии:

(2)

Используя данное условие, запишем выражения для напряжений
на каждом участке и приведём данные выражения к общему знаменателю:

для первого участка ;

для второго участка .

Данное равенство включает в себя переменную первой степени, поэтому запишем выражения для на границах второго участка

- при ;

для третьего участка .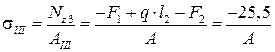

Опасным участком при растяжении-сжатии будет являться такой участок, на котором минимальная площадь сечения и действует максимальная продольная сила.

Принимая в выше указанных выражениях для напряжений знаменатель А за единицу площади, опасным будет являться второй участок при . Для него, по условию прочности (2) выразим площадь сечения:

Зная величину площади второго участка, найдём значения площадей первого и третьего участков:

3. Далее определим величины напряжений:

для первого участка ;

для второго участка:

при ;

для третьего участка .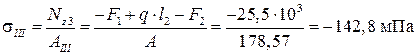

По полученным значениям напряжений строим эпюру ,предварительно выбрав масштабный коэффициент (рис. 3.5).

4. Указываем на стержне характерные точки (рис. 3.5), для которых будем определять величины перемещений . Данные точки лежат
на границах участков.

Рис. 3.5. Схема стержня с построенными эпюрами

Точка А принадлежит жесткой заделке в которой перемещение отсутствует, т. е. .

Для точки В перемещение определится по следующему выражению:

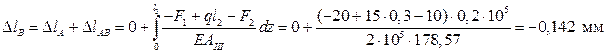
Запишем выражение для перемещения в точке С:

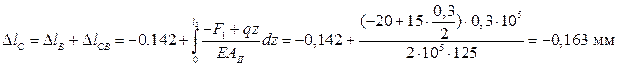
В точке D перемещение определится по выражению:

По найденным величинам перемещений, в выбранном масштабе, строим эпюру .

Задание 3.1. Для стального стержня круглого поперечного сечения, находящегося под действием внешних силовых факторов ( и ), необходимо:

1. определить величины продольных сил на каждом участке стержня
и построить эпюру ;

2. по условию прочности выявить опасный участок стержня
и определить площади каждого участка;

3. определить величины нормальных напряжений на всех участках стержня и построить эпюру s;

4. определить величины перемещений для каждой характерной точки стержня и построить эпюры .

Модуль упругости для стали принять равным ; допускаемое напряжение .

Схемы стержней представлены на рис. 3.6, а исходные данные
в таблице 1.1

Задача 2. Для стального стержня круглого поперечного сечения (рис. 3.7), находящегося под действием сосредоточенных сил F
и распределённой нагрузки , требуются:

1. определить величины реакций в жестких заделках;

2. определить величины продольных сил на каждом участке стержня
и построить эпюру ;

3. по условию прочности выявить опасный участок стержня
и определить площади каждого участка;

4. определить величины нормальных напряжений на всех участках стержня и построить эпюру s;

5. определить величины перемещений для каждой характерной точки стержня и построить эпюры .

Дано:

1. модуль упругости для стали принять равным ;

2. допускаемое напряжение ;

3. ; ;

4. .

Рис. 3.7. Схема стержня

Решение. 1. Исследуемый стержень закреплён с двух сторон жесткими заделками, в которых возникают реакции. По этому, в одной рассматриваемой системе будут иметься две неизвестные (реакции), следовательно система статически неопределима. Для снятия неопределенности необходимо отбросить заделку, а её действие на стержень заменить реактивной силой, которую определяют по уравнению совместности деформаций ().

Обозначим на границах участков стержня характерные точки. Отбросим левую заделку и заменим её действие реакцией связи , представляя её как внешнюю сосредоточенную силу (рис. 3.8).

Рис. 3.8. Схема стержня с отброшенной левой заделкой

Для определения реакции составим следующее уравнение:

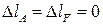, (3)

где - перемещение стержня от приложенных внешних усилий.

Распишем уравнение (3), получим:

. (4)

Перемещение в точке D равно нулю, так как она принадлежит жесткой заделке, т. е. 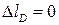. Перемещения на отдельных участках определяется
по зависимости:

. (5)

Используя данную зависимость, уравнение (4) примет вид:

Подставляя в данное уравнение вместо продольных сил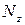
их зависимости, получим:

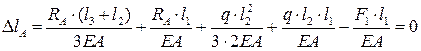. (6)

Выполнив соответствующие преобразования уравнения (6)
и подставив значения длин и силовых параметров выразим реактивную силу :

Далее отбросим правую заделку и заменим её действие реакцией связи (рис. 3.9).

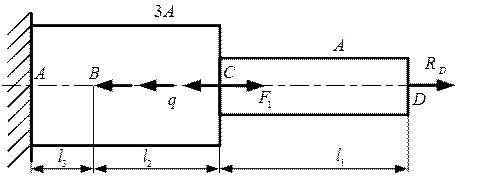
Рис. 3.9. Схема стержня с отброшенной правой заделкой

Для определения неизвестной реакции составим следующее уравнение:

, (7)

Перемещение в точке А равно нулю, так как она принадлежит жесткой заделке, т. е. . Используя зависимость (5), распишем уравнение (7):

Подставляя в данное уравнение вместо продольных сил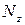
их зависимости, получим:

(8)

Выполнив соответствующие преобразования уравнения (8) и подставив соответствующие значения длин и силовых параметров, найдём величину искомой реакции:

Знак минус указывает на то, что реакция направлена в противоположную сторону.

Выполним проверку правильности определения величин реакций по уравнению равновесия , получим:

Равенство нулю обеих сторон уравнения означает, что реакции найдены верно.

2. Для определения продольных сил, отбросим правую заделку заменив её действие сосредоточенной реакцией и разбив стержень на отдельные участки (рис. 3.13).

Рассмотрим первый участок I - I (рис. 3.10). Его длина изменяется
в следующем пределе . Действие стержня на отсечённый участок заменяем продольной силой , величина которой определится
по следующему уравнению:

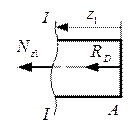
Рис. 3.10. Первый отсечённый участок

Рассмотрим второй участок II - II (рис. 3.11). Его длина изменяется от 0 до ().

(9)

Уравнение (9) является уравнением первой степени, поэтому продольная сила на втором участке будет переменна.

Рис. 3.11. Второй отсечённый участок

Определим величины на границах участка:

- ;

- .

Рассмотрим третий участок III - III (рис. 1.12). Его длина изменяется от 0 до (). Действие стержня на отсечённый участок заменяем продольной силой , величина которой определится по следующему уравнению:

Данное уравнение показывает, что на всём протяжении третьего участка внутренняя продольная сила будет иметь постоянную величину.

Рис. 3.12. Третий отсечённый участок

По полученным величинам продольных усилий строим эпюру , предварительно выбрав масштаб (рис. 3.13).

3. Для определения опасного участка стержня и величин площадей каждого участка, запишем условие прочности при растяжении-сжатии (2)

для первого участка ;

для второго участка: ;

- при ;

для третьего участка .

Зная величину площади второго участка, найдём значения площадей первого и третьего участков:

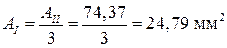
Площадь третьего участка равна по величине площади второго,
т.е. .

3. Далее определим величины напряжений:

для первого участка ;

для второго участка:

при ;

для третьего участка .

По полученным значениям напряжений строим эпюру s,предварительно выбрав масштаб (рис. 3.13).

4. При определении величин перемещений в соответствующих точках стержня рассматриваем его закреплённым с двух сторон жесткими заделками (рис. 3.7). По этому, в точках А и D величины перемещений равны нулю, т. е. и .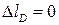

Для точки В перемещение определится по следующему выражению:

В точке С перемещение определится по выражению:

Рис. 3.13. Расчётная схема стержня с эпюрами

Для первого участка запишем:

По найденным величинам перемещений, в выбранном масштабе, строим эпюру (рис. 3.13).

Задание 3.2 Для стального стержня круглого поперечного сечения, находящегося под действием сосредоточенных сил F и распределённой нагрузки , требуются:

1. определить величины реакций в жестких заделках;

2. определить величины продольных сил на каждом участке стержня
и построить эпюру ;

3. по условию прочности выявить опасный участок стержня
и определить площади каждого участка;

4. определить величины нормальных напряжений на всех участках стержня и построить эпюру ;

5. определить величины перемещений для каждой характерной точки стержня и построить эпюры .

Модуль упругости для стали принять равным ; допускаемое напряжение .

Схемы стержней представлены на рис. 3.14, а исходные данные
в таблице 3.1.

Таблица 3.1

Номер варианта

Рис. 3.6

Рис. 3.7

Кручение

Задача 3. Для вала, работающего на кручение (рис. 3.8), необходимо:

1. определить величины крутящих моментов на всех участках вала
и построить эпюру ;

2. по условию прочности определить диаметр опасного сечения вала;

3. определить касательные напряжения на всех участках вала
и построить эпюру касательных напряжений t;

4. определить величины углов закручивания на всех участках вала
и построить эпюру углов закручивания φ;

5. проверить вал по условию жёсткости.

Расчёты провести для вала круглого поперечного сечения, а так же кольцевого сечения. Сравнить результаты и выбрать наиболее рациональное сечение.

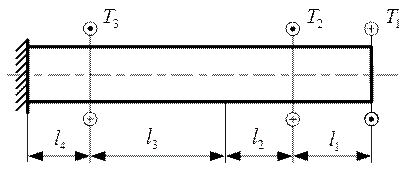
Рис. 3.8. Схема вала

Дано:

1. допускаемое касательное напряжение ;

2. длины участков: ; ; ; ;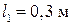

3. крутящие моменты ; ; ;

4. геометрический коэффициент кольцевого сечения .

Решение.

1. Для определения величин внутреннего силового фактора - крутящего момента, разбиваем схему вала на участки, начиная с незакреплённого конца в сторону жёсткой заделки (рис. 3.12). На каждом участке выполняем сечения.

Рассмотрим первое сечения вала I - I (рис. 3.9). Его длина изменяется от 0 до , т. е. 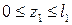. Отсечённый участок уравновешиваем крутящим моментом 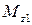, величина которого определится по уравнению:

Рис. 3.9. Первый отсечённый участок вала

Внешний крутящий момент в данном уравнении положителен,
так как при взгляде со стороны сечения он направлен в противоположную сторону хода часовой стрелки.

На втором участке (сечение II - II) действует уже несколько внешних крутящих моментов (рис. 3.10). Длина участка изменяется в пределе . Отсечённый участок уравновешиваем моментом , который определится по следующему уравнению:

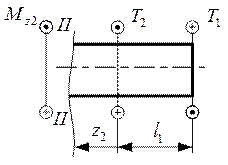
Рис. 3.10. Второй отсечённый участок вала

Длина третьего участка изменяется от 0 до , т. е. . Уравновесим отсечённый участок (рис. 3.10) крутящим моментом , величина которого определится по следующему уравнению:

Рис. 2.3. Третий отсечённый участок вала

Так как на третьем участке не действуют внешние крутящие моменты, то уравнение для определения внутреннего силового фактора получилось подобным уравнению для предшествующего второго участка.

Рассмотрим четвертый участок, длина которого изменяется в пределе (рис. 2.4). Уравновесим отсечённый участок моментом
и определим его величину по уравнению:

Рис. 2.4. Четвёртый отсечённый участок вала

По найденным величинам крутящих моментов строим эпюру , выбрав соответствующий масштаб (рис. 2.5)

2.1 Выполним следующие пункты задания (2÷5) для вала круглого поперечного сечения.

Запишем условие прочности при кручении, которое имеет вид:

, (1)

где - расчётное касательное напряжение в сечениях вала; - полярный момент сопротивления сечения; - допускаемое напряжение при кручении.

Полярный момент сопротивления для круглого поперечного сечения является его геометрической характеристикой, и определятся по следующей зависимости:

. (2)

Подставляя зависимость (2) в условие прочности (1), получим:

. (3)

Выбираем опасное сечение вала. Опасным сечением при постоянной площади вала будет являться такое, в котором действует наибольший крутящий момент. В нашем случае, опасным будет являться сечение на четвёртом участке, так как на нём действует максимальный внутренний силовой фактор . Для него найдём величину диаметра вала

Определим диаметр вала в опасном сечении из преобразованного условия прочности (2.3):

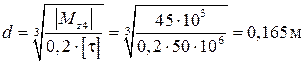Следовательно, площадь исследуемого сечения вала будет равна:

3.1 Диаметр рассматриваемого вала на каждом его участке будет одинаковым. Зная величину диаметра, определим касательные напряжения:

на первом участке ;

на втором участке: ;

на третьем участке: ;

на четвёртом участке: .

По полученным величинам касательных напряжений строим эпюру
(рис. 2.5).

4.1 Для определения величин углов закручивания проставляем характерные точки на границах участках вала (рис. 2.5) и рассматриваем вал с закреплённого его участка в сторону свободного конца.

Угол закручивания определяется по формуле:

, (4)

где - длина исследуемого участка вала; - модуль сдвига; - полярный момент инерции.

Для круглого поперечного сечения полярный момент инерции определится по формуле:

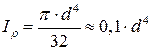В нашем случае величина будет равна:

Зная величины модуля сдвига и полярного момента инерции, определим величин углов закручивания сечений вала используя формулу (4).

Точка А принадлежит жёсткой заделке, следовательно деформация
в данной точке равна нулю, т. е. .

В точке В угол закручивания будет равен:

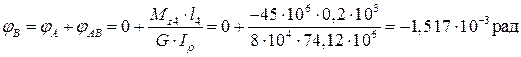
Для точки С получим:

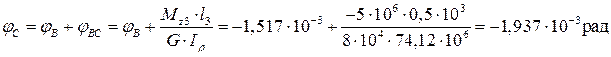
В точке D угол закручивания определится следующим образом:

Для точки Е получим:

По найденным величинам углов закручивания и выбрав соответствующий масштаб, строим эпюру .

5.1 Проверяем вал по условию жесткости, которое выглядит
в следующем виде:

, (5)

где - относительный угол закручивания; - допускаемый угол закручивания.

Величина допускаемого угла закручивания в большинстве случаев принимается конструктивно и зависит от длины вала. В технических конструкциях машиностроительного производства .

В нашем случае, максимальный крутящий момент действует
на четвёртом участке . Следовательно, относительный угол закручивания на данном участке определится
по выражению:

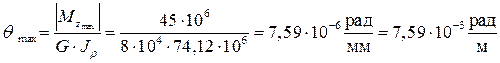Расчетный угол закручивания в опасном участке получился
по величине меньше, чем допускаемый угол. Следовательно, можно сделать вывод, что условие жёсткости выполняется.

2.2 Далее выполним пункты задания (2÷5) для вала кольцевого сечения.

Определяем внешний и внутренний диаметры вала в опасном участке из условия прочности (1) при кручении. В нашем примере, опасным является сечение на четвёртом участке, с крутящим моментом равным .

Значение внешнего диаметра вала кольцевого сечения будет определяться по выражению:

Величина внутреннего диаметра определится по следующей зависимости:

Зная величины диаметров кольцевого сечения, найдём его площадь:

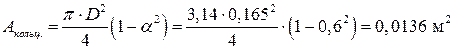3.2 Полярный момент сопротивления кольцевого сечения равен:

Зная величину , определим касательные напряжения на каждом участке вала:

на первом участке ;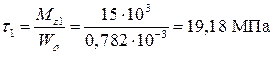

на втором участке: ;

на третьем участке: ;

на четвёртом участке: .

По найденным значениям касательных напряжений строим эпюру
(рис. 2.5) выбрав соответствующий масштаб.

Анализируя значения, видно, что на четвёртом участке условие прочности не выполняется:

Чтобы условие выполнялось, необходимо увеличить площадь сечения вала на данном участке.

4.2 Определяем углы закручивания сечений вала по формуле (4), рассматривая вал с закрепленного конца.

Полярный момент инерции для кольцевого сечения определится
по формуле:

Деформация в точке А равна нулю ().

В точке В угол закручивания будет равен:

Для точки С получим:

В точке D угол закручивания равен:

Для точки Е получим:

По найденным величинам углов закручивания и выбрав соответствующий масштаб, строим эпюру .

Рис. 2.5. Схема вала с эпюрами

5.2 Проверим вал по условию жесткости (5) для опасного участка:

Условие жёсткости выполняется.

6. Более рациональным, с точки зрения использования материала, будет такое сечение, у которого наименьшая площадь. В нашем случае отношение величин площадей выглядит следующим образом:

Значит площадь кольцевого сечения в раз меньше, чем круглое поперечное, а следовательно и рациональнее.

Однако, с точки зрения выполнения условий жёсткости и прочности, рациональным будет круглое поперечное сечение вала, так как для него
все условия выполняются. Для кольцевого сечения условие прочности
не выполняется, следовательно, использовать его при заданных параметрах нагружения нельзя.

Задание 2.1 Для вала, работающего на кручение,

Воспользуйтесь поиском по сайту: