Оценка площади охлаждающей поверхности радиатора

Микросхема УМЗЧ обязательно должна быть установлена на радиаторе – ведь даже в состоянии покоя на ней рассеивается мощность, равная P0=UпI0=(2•25)•0,07=3,5 Вт. Чтобы рассчитать необходимую площадь радиатора, вычислим максимальную рассеиваемую мощность для случая работы в идеальном классе В:
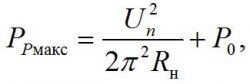где Uп – полное напряжение источника питания, Rн – сопротивление нагрузки, Р0 – мощность, рассеиваемая в режиме покоя.
При полном напряжении источника питания Uп =50 В, Rн =8 Ом на корпусе микросхемы должна рассеиваться мощность около 19,3 Вт. Ясно, что температура кристалла при работе всегда должна быть ниже 150ºС. Примем температуру окружающего воздуха 53 ºС, тогда тепловое сопротивление переход – окружающая среда должно быть меньше, чем: (150-53)/19,3=5,0 ºС/Вт.

Обычно сумма тепловых сопротивлений корпус – радиатор и радиатор – окружающая среда оказываются меньше, чем 2,0 ºС/Вт. Тепловое сопротивление корпус – радиатор зависит от способа установки микросхемы. Если использовано непосредственное соединение металл – металл, тепловое сопротивление будет примерно 1,0 ºС/Вт при использовании теплопроводной пасты и 1,2 ºС/Вт при ее отсутствии.

При наличии слюдяной прокладки между корпусом и радиатором тепловое сопротивление можно считать равным 1,6 ºС/Вт и 3,4 ºС/Вт соответственно при применении теплопроводной пасты и без нее. Рассмотрим для примера крепление микросхемы к радиатору через слюдяную прокладку с применением теплопроводной пасты. Тепловое сопротивление радиатора должно быть меньше чем 5,0 – 2,0 - 1,6 = 1,4 ºС/Вт. Это рекомендуемое тепловое сопротивление радиатора для данной конструкции.

Полезно оценить результаты расчетов радиатора с помощью какой-нибудь программы, например, [4]. Самый прикидочный расчет площади охлаждающей поверхности радиатора: 20 квадратных сантиметров на каждый ватт рассеиваемой микросхемой мощности.
Для радиаторов, выполненных из алюминиевых сплавов с ребрами не тоньше 3 мм при шаге ребер не менее 10 мм и свободном потоке воздуха площадь радиатора можно оценить следующей приближенной формулой: S[кв см]≈600/Rθр-с[ºС/Вт]=600/1,4=430 кв см.
Как уже указывалось, микросхема LM1875 снабжена эффективной схемой тепловой защиты. Когда температура кристалла микросхемы достигнет 170 ºС, схема тепловой защиты срабатывает, и усилитель выключается. Включение происходит после понижения температуры кристалла до 145 ºС. Однако, если температура кристалла снова начнет повышаться, то теперь отключение произойдет уже при 150 ºС.

 

http://proacustic.ru/teplootvod.html

 

ОУ, выходная мощность которых превышает 1 Вт, обычно требуют установки теплоотвода (радиатора) для охлаждения кристалла. Напомню, что усилитель, работающий в режиме AB, имеет КПД около 50%. Это означает, что он выделяет столько же мощности в виде тепла, сколько отдает в нагрузку. Поэтому для охлаждения кристалла микросхемы (транзистора) необходимо использовать теплоотвод.

Максимальная температура, при которой кристалл близок к разрушению, но еще сохраняет работоспособность, составляет 150 °С. При этом температура корпуса ниже в связи с тепловыми потерями при переходе от кристалла к корпусу и, как правило, не превышает 100 °С. Нормальная температура кристалла составляет 75 °С, а радиатора -50-60 °С. Такая температура соответствует болевому порогу кожи человека, поэтому есть очень простое правило: если вы не обжигаетесь, коснувшись радиатора рукой, его температура находится в норме (конечно, при условии хорошего контакта между радиатором и тепловыделяющим элементом).

Стоит также отметить, что срок службы микросхемы напрямую зависит от ее температуры. Существует правило, гласящее, что при увеличении температуры кристалла на 10 °С срок его службы падает вдвое. Это значит, что при увеличении температуры кристалла с 60 до
100 °С срок его службы снизится уже в 1 б раз! Поэтому эффективное.охлаждение — залог надежной и долгой работы устройства.

Радиаторы, используемые для охлаждения радиоэлементов, классифицируются по строению на:

• ребристые (рис. 2.17, а);

• игольчатые (рис. 2.17, б).
По типу вентиляции:

• с естественной вентиляцией;

• с принудительной вентиляцией.

Эти типы радиаторов отличаются плотностью расположения ребер или игл. Для радиаторов с естественной вентиляцией расстояние между ребрами (иглами) должно быть не менее 4 мм. К тому же такие радиаторы рассчитаны для работы только в вертикальном положении, когда воздух под действием естественных сил движется между ребрами. Если расстояние между ребрами (иглами) составляет около 2 мм, то такой радиатор рассчитан на принудительную вентиляцию и требует установки вентилятора.

По применяемым материалам:

• цельные алюминиевые;

• цельные медные;

• алюминиевые с медным основанием.

Существуют методики точного расчета радиаторов, учитывающие рассеиваемую мощность, параметры окружающей среды, конфигурацию, материал радиатора и т.д. Однако эти методики нужны на этапе проектирования теплоотвода. Радиолюбители редко самостоятельно изготавливают радиаторы, чаще используя готовые, взятые из старой радиоаппаратуры. В конечном итоге нас интересует только один параметр — максимальная рассеиваемая мощность для этого радиатора. Чтобы определить его, достаточно знать всего две характеристики: тип
вентиляции и площадь рассеивающей поверхности (проще говоря, площадь радиатора).

Площадь ребристого радиатора вычисляется как сумма площадей всех его ребер и площади основания. Заметьте, что у одного ребра две излучающие поверхности. Это значит, что ребро размером 1×1 см имеет площадь 2 см2. Площадь игольчатого радиатора вычисляется как сумма площадей всех его игл и площади основания. Площадь одной иглы можно вычислить по формуле:

S = π ( r ₁ + r ₂ ) l

(r₁ - радиус нижнего основания усеченного конуса; r₂ - радиус верхнего основания усеченного конуса; l - образующая усеченного конуса (длина боковой стороны))

После этого допустимая рассеиваемая мощность может быть оценена по формуле:

где Р — допустимая рассеваемая мощность, Вт; S — площадь радиатора, см2; к — коэффициент, учитывающий тип вентиляции. Для естественной вентиляции к = 33, для принудительной вентиляции к = 11.

Тепловое сопротивление радиатора может быть оценено по формуле Rth=(51*k)/S, описанной здесь: http://forum.cxem.net/index.php?showtopic=32031

Размерность теплового сопротивления - градус/Ватт. То есть насколько температура кристалла будет выше температуры корпуса при выделении 1 Вт тепла.
Тепловое сопротивление перехода корпус - окружающая среда можно посчитать по приблизительной формуле: Rth=(51*k)/S, где Rth – тепловое сопротивление радиатора в C/W, S – площадь радиатора (в данном случае - площадь детали) в см2, k – коэффициент, учитывающий тип вентиляции (Для естественной вентиляции k = 33, для принудительной вентиляции k = 11).
Тепловые сопротивления детали и радиатора нужно сложить, задать температуру окружающей среды и выделяемую мощность, чтобы получить температуру кристалла.
Чтобы не ломать сильно голову по поводу теплопроводности материалов, скажу что тепловое сопротивление перехода кристалл - корпус обычно находится в пределах от 1 C/W для мощных ИС, и до 3 C/W для маломощных.

В последние годы в радиолюбительской практике все чаще применяются системы охлаждения для процессоров персональных компьютеров (cooler — кулеры). Кулеры современных процессоров рассчитаны на рассеивание мощности около 100 Вт даже при небольшой вентиляции.

Для крепления микросхемы к основанию радиатора можно использовать шурупы с плоской шляпкой либо, при наличии метчика, нарезать резьбу в радиаторе и закрепить микросхему винтом. Между основанием радиатора и корпусом микросхемы обязательно должен быть слой термопасты для улучшения теплопроводности. Наилучшие показатели теплопроводности показывают пасты типа КПТ-81 или «Алсил-3». Их можно купить в любом компьютерном магазине или магазине радиодеталей. Теплопроводность термопаст составляет при-
мерно 0,7- с учетом того, что площадь контакта — 1 -2 см2, тепловое сопротивление термопасты — примерно 10~4 °С/Вт (несоизмеримо мало по сравнению с тепловым сопротивлением перехода кристалл-подложка либо радиатора и окружающей среды), поэтому при тепловом расчете системы охлаждения этой потерей можно пренебречь.

http://forum.cxem.net/index.php?showtopic=32031

Что бы совсем разобратся нужно на конкретном примере. К примеру есть ИМС длина 2см ширина 1см толщина 0,5 см Мощность 535 мВт Температура воздуха 22 по цельсию. Как считать?

 

1. Определяем излучающую площадь микросхемы. Учтем, что она брюхом скорее всего будет прилегать к плате, так что там конвекции не будет. Возьмем эквивалентную площадь брюха как ½ от геометрической площади:
   2(2*0,5)+2(1*0,5)+1*2+1*1=2+1+2+1=6 см2 – полная излучающая площадь микросхемы
   2. Подсчитаем тепловое сопротивление перехода корпус – воздух:
   Rth=(51*k)/S=(51*33)/6=280,5 C/W
   3. Микросхема судя по всему маломощная, прими её тепловое сопротивление равным 3 C/W (или можно рассчитать точно, если знаете как)
   4. Общее тепловое сопротивление равно 280,5+3=283,5 C/W Это значит что температура кристалла будет на 283,5 градуса выше температуры окр. среды при выделении 1 Вт. тепла.
   5. Определяем температуру кристалла: 283,5*0,535+22=173 =)
   6. Определяем температуру корпуса: 280,5*0,535+22=172
   
   Резонный вопрос – есть ли здесь ошибка? Ошибка может быть в определении Rth корпуса микросхемы... эта формула используется для определения теплового сопротивления ребристых радиаторов, по этому в области малых значений площади может давать не верный результат. Еще недостатком методики является то, что мы не учитываем охлаждения микросхемы через саму плату.
   
   P.S. хотя если предположить, что микросхема обдувается (k=11). то получается вполне вменяемый результат - 93 C/W
   
   

 

123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: