Когда рекурсию использовать не нужно

Введение

Рекурсивным называется объект, частично состоящий или определяемый с помощью самого себя. Рекурсия встречается не только в математике, но и в повседневной жизни.

Рекурсивные определения в математике представляют со мощный аппарат. Вот несколько общеизвестных примеров: натуральные числа, деревья и определенные функции.

1. Натуральные числа:

а) 0 есть натуральное число,

б) число, следующее за натуральным, есть натуральное число.

2. Деревья:

а) 0 есть дерево (его называют "пустым деревом"),

б) если t1 и t2 – деревья, то построение, содержащее вершину с двумя ниже расположенными деревьями, опять же дерево.

3. Функция "факториал" п\ (для неотрицательных целых чисел):

а) 0! = 1,

б) n>0:n! = n*(n- 1)!

Мощность рекурсивного определения заключается, очевидно, в том, что оно позволяет с помощью конечного высказывания оп­ределить бесконечное множество объектов. Аналогично с помощью конечной рекурсивной программы можно описать беско­нечное вычисление, причем программа не будет содержать явных повторений. Однако рекурсивные алгоритмы лучше всего исполь­зовать, если в решаемой задаче, вычисляемой функции или струк­туре обрабатываемых данных рекурсия уже присутствует явно. В общем виде рекурсивную программу Р можно выразить как не­которую композицию Р из множества операторов S (не содержащих Р) и самой Р:

P= P [ S,P]. (3.1)

Для выражения рекурсивных программ необходимо и достаточ­но иметь понятие процедуры или подпрограммы, поскольку они позволяют дать любому оператору имя, с помощью которого к нему можно обращаться. Если некоторая процедура Р содержит явную ссылку на саму себя, то ее называют прямо рекурсивной, если же Р ссылается на другую процедуру Q, содержащую (прямую и косвенную) ссылку на Р, то Р называют косвенно рекурсивной. Поэтому по тексту программы рекурсивность не всегда явно определима.

Как правило, с процедурой связывают множество локальных объектов, т. е. множество переменных, констант, типов и процедур, которые определены только в этой процедуре и вне ее не существуют или не имеют смысла. При каждой рекурсивной активации такой процедуры порождается новое множество ло­кальных связанных переменных. Хотя они имеют те же самые имена, что и соответствующие элементы локального множества предыдущего "поколения" этой процедуры, их значения отлич­ны от последних, а любые конфликты по именам разрешаются с помощью правил, определяющих область действия идентифи­каторов: идентификатор всегда относится к самому последнему порожденному множеству переменных. Это же правило справедливо и для параметров процедуры, по определению связанных с самой процедурой.

Подобно операторам цикла, рекурсивные процедуры могут приводить к незаканчивающимся вычислениям, и поэтому на эту проблему следует особо обратить внимание. Очевидно, чтобы работа когда-либо завершилась, необходимо, чтобы рекурсивное обращение к Р управлялось некоторым условием, которое в какой-то момент перестает выполняться. Поэтому более точно схему рекурсивных алгоритмов можно представить в из следующих форм:

Р= IF В THEN P [S, P] END,

P = Р [S, IF В THEN P END].

Основной способ доказательства конечности некоторого повторяющегося процесса таков:

1. Определяется функция f(х) (х – множество переменных) такая, что из f(х) < 0 следует истинность условия окончания цикла (с предусловием или постусловием).

2. Доказывается, что при каждом прохождении цикла f(x) уменьшается.

Аналогично доказывается и окончание рекурсии – noказывается, что Р уменьшает f(x), такую, что из f(x) £ 0 следует –В. В частности, наиболее надежный способ обеспечить окончание процедуры – ввести в нее некоторый параметр (значение), назовем его n, и при рекурсивном обращении к Р в качестве пара задавать n – 1. Если в этом случае в качестве В используется n>0, то окончание гарантировано. Это опять же выражается двумя схемами:

Р(п) = IF п > О THEN P [ S, Р (n – 1)] END,

P (р) = Р [ S, IF п > О THEN Р(п – 1) END].

В практических приложениях важно убедиться, что максимальная глубина рекурсий не только конечна, но и достаточно, Дело в том, что каждая рекурсивная активация процедуры P требует памяти для размещения ее переменных. Кроме этих локальных переменных нужно еще сохранять текущее "состояние вычислений", чтобы можно было вернуться в него по окончании новой активации Р.

 

Когда рекурсию использовать не нужно

Рекурсивные алгоритмы особенно подходят для задач, где обрабатываемые данные определяются в терминах рекурсии. Однако это не означает, что такое рекурсивное определение данных гарантирует бесспорность употребления для решения задачи рекурсивного алгоритма. Фактически объяснение концепций рекур­сивных алгоритмов на неподходящих для этого примерах и вызвало широко распространенное предубеждение против использования рекурсий в программировании; их даже сделали синонимом неэффективности.

Программы, в которых следует избегать алгоритмической рекурсии, можно охарактеризовать некоторой схемой, отражающей их строение (специфично, что тут есть единственное обращение к Р в конце или начале всей конструкции):

Pº IF В THEN S; P END, (3.6)

Pº S; IF В THEN P END. (3.7)

Такие схемы естественны в ситуациях, где вычисляемые значения определяются с помощью простых рекуррентных отношений. Возьмем хорошо известный пример вычисления факториала

i=0,1,2,3,4,5,...,

f_i =1, 1, 2, 6, 24, 120,....

Первое из чисел определяется явно – f₀ = 1, а последующие определяются рекурсивным образом с помощью предшествующего числа:

Такое рекуррентное отношение предполагает рекурсивный алгоритм вычисления n-го факториального числа. Если мы введем две переменные i и f, обозначающие на i-м уровне рекурсии, то обнаружим, что для перехода к следующему числу последовательности нужно проделать такие вычисления:

i++; f*=i;

откуда получаем простую рекурсивную программу:

Однако более часто употребляется и полностью эквивалентна ей запись, где вместо Р приведена так называемая процедура-функция, т. е. процедура, с которой связывается значение–результат и которую поэтому можно применять прямо как составляющую выражения. В этом случае переменная F становится излишней, а роль i явно выполняет параметр процедуры:

PROCEDURE F (I: INTEGER): INTEGER; BEGIN

IF I > 0 THEN RETURN I*F(I-1) ELSE RETURN 1 END END F;

Теперь уже ясно, что в нашем примере рекурсия крайне просто заменяется итерацией. Это проделано в такой программе:

I:= 0; F: = 1;

WHILE I < n DO I:= 1+1; F:= I*F END;

Конечно, существуют и более сложные схемы рекурсий, которые можно и необходимо переводить в итеративную форму. Возьмем в качестве примера вычисление чисел Фибоначчи, определяемых рекурсивным соотношением

fib_n+1 =fib_n + fib_n–i для n > 0 (3.16)

и fib₁ =1; fib₀ =0.

Прямое, "наивное", переписывание приводит к рекурсивной программе:

PROCEDURE Fib(i: INTEGER): INTEGER;

BEGIN

IF n = 0 THEN RETURN 0

ELSIF n = 1 THEN RETURN 1 (3.17)

ELSE RETURN Fib(n-1)+Fib{n-2)

END

END Fib;

Вычисление fib путем обращения к Fib(n) приводит к рекурсивным активациям этой процедуры-функции. Как часто это происходит? Каждое обращение с п > 1 приводит еще к двум обращениям, т. е. общее число вызовов растет экспоненциально (рис. 3.2).

Ясно, что такая программа практического интереса не представляет.

Однако, к счастью, числа Фибоначчи можно вычислять и по итеративной схеме, где с помощью вспомогательных переменных х = fib_i и у = fib_i-i удается избежать повторных вычислений одной и той же величины:

i = 1; х = 1; у = 0;

WHILE i < n DO z = х; х+ = y, у:= z; i++ END;

Итак, урок таков: следует избегать рекурсий там, где есть очевидное итерационное решение. Однако это не означает, что от рекурсий следует избавляться любой ценой. Существует много хороших примеров применения рекурсии, что мы и продемонстрируем в последующем. То, что существует реализации рекурсивных процедур на фактически нерекурсивных машинах, доказывает, что для практических целей любую рекурсивную программу можно трансформировать в чисто итеративную. Однако это требует явной работы со стеком для рекурсий, причем эти действия часто настолько затуманивают суть программы, что ее бывает трудно понять. Вывод: алгоритмы, рекурсивные по своей природе, а не итеративные, нужно формулировать как рекурсивные процедуры.

3. Два примера рекурсивных программ

Симпатичный узор на рис. 3.3 состоит из суперпозиции пяти кривых. Эти кривые соответствуют некоторому регулярному образу и считается, что их можно нарисовать на экране дисплея или на графопостроителе под управлением какой-либо вычислительной машины. Наша задача – найти рекурсивную схему, по которой можно было бы создать программу для такого рисования. Рассматривая рис. 3.3, мы обнаруживаем, что три наложенные друг на друга кривые имеют форму, показанную на рис. 3.4; обозначим их через H₁, H₂ и H_3.. Видно, что H_i+1 получается соединением четырех экземпляров H_i вдвое меньшего размера, повернутых соответствующим образом и «стянутых» вместе тремя прямыми линиями. Заметим, что Н₁ можно считать состоящей из четырех вхождений пустой H₀, соединенных этими же тремя линиями. Кривая H_i называется кривой Гильберта i-го порядка в честь ее первооткрывателя Д. Гильберта (1891 г.).

Поскольку каждая кривая H_i состоит из четырех вдвое меньших H_i–1, то процедура для рисования H_i будет включать четыре обращения для рисования H_i–1 соответствующим образом повернутых и уменьшенных вдвое. Для наглядности мы обозначим эти четыре части через A, В, С и D, а процедуры, рисующие соединительные прямые, будем обозначать стрелками, указывающими соответствующее направление. В этом случае появляется такая схема рекурсий (см. рис. 3.4):

Представим себе, что для рисования части прямой в нашем распоряжении есть процедура line, передвигающая перо в заданном направлении на заданное расстояние. Для удобства будем предполагать, что направление задается целым параметром i как 45´ i градусов. Если единичную длину прямой обозначить че­рез u, то с помощью рекурсивных обращений к аналогично составленным процедурам для В и D и к самой А легко написать процедуру, соответствующую схеме А:

PROCEDURE A(i: INTEGER);

BEGIN

IF i > 0 THEN

D(i-1); line{4,u);

A(i-l); line(6,u);

A(i-1); line(0,u);

B(i-1)

END

END A;

Эта процедура инициируется главной программой по одному разу для каждой из кривых Гильберта, образующих приведенный на рис. 3.4 узор. Главная программа определяет начальную точ» кривой, т. е. исходные координаты пера (Р_х и Р_у) и единичное приращение u. Заданного размера квадрат, где рисуется кривая, помещается в середине страницы (см. рис. 3.5). Величина h₀ должна удовлетворять равенству h₀ = 2^k для некоторого k ³ n. Эти параметры, так же как и процедура рисования прямой, находятся в модуле с названием LineDrawing. Программа рисует n кривых Гильберта – H₁,. H₂, ¼, H_n (см. листинг 3.1 и рис. 3.4).

Кривые Гильберта

MODULE Hilbert;

FROM Terminal IMPORT Read;

FROM LineDnwing IMPORT width, height, Px, Py, clear, line;

CONST SquareSize = 512;

UNSIGNED i, x0, y0, u;

CHAR ch;

PROCEDURE A(i)

BEGIN

IF i>0 THEN

D(i-1); line(4,u); A(i-1); line(6,u);

A(i-1); line(0,u); B(i-1);

END A;

PROCEDURE B(i)

BEGIN

IF i>0 THEN

C(i-1); line(2,u); B(i-1); line(0,u);

B(i-1); line(6,u); A(i-l)

END B;

PROCEDURE C(i)

BEGIN

IF i>0 THEN

B(i-1); line(0,u); C(i-1): line(2,u);

C(i-l); line(4,u); D(i-1)

END C;

PROCEDURE D(i)

BEGIN

IF i>0 THEN

A(i-1); line(6,u); D(i-1); line(4,u);

D(i-1); line(2,u); C(i-l)

END D;

BEGIN clear;

x0 = width >> 1; y0 = height >> 1;

u=SquareSize; i=0;

DO

{

i++;

u>>1;

x0+=(u>>1); y0+=(u>>1);

Px=x0; Py=y0: A(i); Read(ch)

UNTIL (ch = 33C)||(i=6);

END Hilbert

Подобный, но более сложный и эстетически утонченный пример приводится на рис. 3.7. Он также получен путем наложения друг на друга нескольких кривых. Первые две из них показаны на рис. 3,6. Кривая S_i называется кривой Серпинского i-го порядка. Какова же рекурсивная схема этих кривых? Попробуем в качестве основного строительного блока взять S_i, возможно, без одного ребра. Это не приведет нас к решению. Главное отличие кривой Серпинского от кривой Гильберта состоит в том, что первая замкнута (и в ней нет пересечений). Это означает, что основная рекурсивная схема должна давать разомкнутую кривую, четыре части которой соединяются линиями, не принадлежащими самому рекурсивному образу. И действительно, эти замыкающие линии представляют собой отрезки прямых в четырех внешних углах (на рис. 3.6 они выделены жирными линиями). Можно считать, что они принадлежат к непустой начальной кривой S – квадрату, «стоящему» на одном углу. Теперь легко составить рекурсивную схему. Четыре составляющих образа вновь обозначим через А, B, С, D, а связывающие линии будем рисовать явно. Обратите внимание: четыре рекурсивных образа по существу идентичны, они лишь поворачиваются на 90°.

Основной образ кривых Серпинского задается схемой

а рекурсивные составляющие (горизонтальные и вертикальные отрезки – удвоенной длины) – схемой

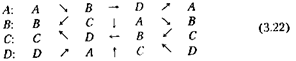
Если использовать те же примитивы рисования, что и в случае кривых Гильберта, то приведенные рекурсивные схемы без труда трансформируются в (прямо или косвенно) рекурсивный алгоритм.

PROCEDURE A(INT k);

BEGIN

IF k>0 THEN

A(k-1); line(7,h);

B(k-1); line(0,2*h);

D(k-1); lined,h); A(k-1)

END A;

Эта процедура порождается из первой строки рекурсивной схемы (3.22). Аналогично получаются и процедуры, соответствую­щие образам В, С и D. Главная программа строится по образу (3.21). Ее задача – установить начальные значения для координат рисунка и задать единичную длину линий h; это все зависит от формата бумаги (листинг 3.2). На рис. 3.7 приведен результат работы такой программы с n = 4.

Ясно, что в этих примерах рекурсия используется элегантным способом. Правильность программ легко подтверждается их структурой и формируемыми образами. Кроме того, употребление в соответствии со схемой (3.5) явного параметра для уровня гарантирует окончание работы, так как глубина рекурсии не может быть больше n. По сравнению с таким рекурсивным построением эквивалентные программы, где избегали употребления рекурсии, выглядят крайне сложными и запутанными.

Листинг 3.2. Кривые Серпинского

MODULE Sierpinski;

FROM Terminal IMPORT Read:

FROM lineDrawing IMPORT width, height, Px, Py, clear, line;

CONST SquareSize = 512;

UNSIGNED i, h, x0, y0;

CHAR ch;

PROCEDURE A(k);

BEGIN

IF k>0 THEN

A(k-1); line(7, h); B(k-1), line(0, 2*h);

D(k-1); lined, h); A(k-1)

END A;

PROCEDURE B(k);

BEGIN

IF k>0 THEN

B(k-1); line(5, h); C(k-1); line(6, 2*h);

A(k-1); line(7, h); B(k-1)

END B;

PROCEDURE C(k);

BEGIN

IF k>0 THEN

C(k-1); line(3, h): D(k-1); line(4, 2*h);

B(k-1); line(5. h); C(k-1)

END C;

PROCEDURE D(k);

BEGIN

IF k>0 THEN

D(k-1); lined, h); A(k-1); line(2, 2*h);

C(k-1); line(3, h); D(k-1)

END D;

BEGIN

clear;

i = 0; h = SquareSize>>2;

x0 = width >> 1; y0 = height >> 1 + h;

DO i++: x0-=h;

h>>1; yO+=h; Px = x0: Py = y0;

A(i): line(7, h); B(i); line(5, h):

C(i): line(3, h); D(i); line(1, h); Read(ch)

UNTIL (i = 6) || (ch = 33C);

 

clear

END Sierpinski.

4. Алгоритмы с возвратом

Особенно интригующая область программирования – задачи так называ­емого искусственного интеллекта. Здесь алгоритмы ищут решение задачи не по заданным правилам вычислений, а путем проб и ошибок. Обычно процесс проб и ошибок разделяется на отдельные задачи. Часто эти задачи наиболее естественно выражаются в терминах рекурсии и требуют исследования конечного числа подзадач. В общем виде весь процесс мозно мыслить как процесс поиска, строящий (и обрезающий) дерево подзадач. Во многих проблемах такое дерево поиска растет очень быстро, рост зависит от параметров задачи и часто бывает экспоненциальным. Соответственно увеличивается и стоимость поиска. Иногда, используя некоторые эвристические приемы, дерево поиска удается сократить и тем самым свести затраты на вычисления к разумным пределам.

Например, часто встречается построение с явным параметром параметром для уровня, когда указывается глубина рекурсии. Это приводит к простым условиям окончания работы. Более того, если на каждом шаге число исследуемых путей фиксировано (пусть оно равно m), то можно применять следующую схему, к которой можно обращаться с помощью оператора Try(1):

Procedure Try(i);

int k;

Begin

k=0;

Do

k++; // выбор k-го кандидата

If подходит Then

его запись;

If i<n Then

Try(i+1);

If неудача Then стирание записи;

Until удача || (k=m);

End Try;

В качестве примеров данных алгоритмов с возвратом можно указать следующие:

1) Задача о шахматном коне, который должен, стартовав на произвольном поле доски размера n´n, обойти всю доску побывав на каждом поле не более одного раза.

2) Задача о расстановке n ферзей на шахматной доске размера n´n, чтобы ни один ферзь не находился под боем другого.

3) Задача о стабильных браках.

4) Задача оптимального выбора.

Они будут вам предложены в качестве домашних заданий.

 

 

Поделиться:

Воспользуйтесь поиском по сайту: