 |
Задача на собственные значения для вырождающегося уравнения смешанного типа
|
|
|
|
Сабитов К.Б., Бибакова С.Л.
1. Постановка задачи. Рассмотрим уравнение:
 (1)
(1)
где  l - комплексный параметр, в области D, ограниченный при
l - комплексный параметр, в области D, ограниченный при  кривой
кривой 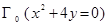 с концами в точках B (1, 0) и K (0, 1/4), лежащей в первом квадранте, отрезком AK оси OY, где A=(0, 0), и характеристиками AC (
с концами в точках B (1, 0) и K (0, 1/4), лежащей в первом квадранте, отрезком AK оси OY, где A=(0, 0), и характеристиками AC ( ) и CB (
) и CB ( ) уравнения (1) при
) уравнения (1) при  .
.
Пусть 
Задача Tl. Найти значения параметра  и соответствующие им функции
и соответствующие им функции  , удовлетворяющие условиям:
, удовлетворяющие условиям:
 (2)
(2)
 (3)
(3)
 (4)
(4)
 (5)
(5)
где  при
при 
 при
при 
Выбор значения k таковым объясняется тем, что для уравнения (1) при  доказаны теоремы существования и единственности решения задачи Трикоми [1].
доказаны теоремы существования и единственности решения задачи Трикоми [1].
Спектральные задачи для оператора Лаврентьева-Бицадзе были рассмотрены в работах [2-4].
В работах [5-8] изучены спектральные задачи для уравнения (1) с условиями Дирихле. В [5] для уравнения (1) в области эллиптичности построены решения первой краевой задачи и смешанной краевой задачи с помощью биортогональных рядов. В работе [6] уравнение (1) рассматривалось в D, где подобласть D+ ограничена отрезком NB оси y=0, N=(-1, 0), и дугой NB:  а в работах [7-8] уравнение (1) изучалось в D при
а в работах [7-8] уравнение (1) изучалось в D при 
В данной работе найдены в явном виде собственные значения и соответствующие собственные функции, которые отличаются от результатов [6].
2. Построение частных решений в области эллиптичности. В области D+ перейдем к новым переменным 
 ,
,  В координатах
В координатах 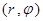 уравнение (1) примет вид:
уравнение (1) примет вид:

где  .
.
Разделяя переменные  получим:
получим:
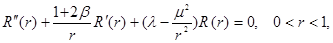 (6)
(6)
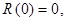
 (7)
(7)
 (8)
(8)
 (9)
(9)
Известно [1], что решением уравнения (6) является функция Бесселя
 (10)
(10)
Удовлетворяя (10) краевым условиям (7) и (8), имеем:
 (11)
(11)
Теперь построим общее решение для уравнения (8). Для этого в (8) введем новую переменную 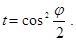 Тогда оно примет вид:
Тогда оно примет вид:
|
|
|
 (12)
(12)
Уравнение (12) является гипергеометрическим уравнением [9, с. 69], и поскольку a не является целым числом, то общее решение уравнения (8) определяется по формуле
 (13)
(13)
Функция (13) удовлетворяет первому граничному условию из (9). Удовлетворим (13) второму краевому условию из (9).
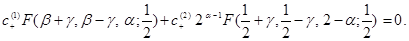 (14)
(14)
На основании равенств [10, с. 112]

имеем уравнение для нахождения неизвестного  :
:
 (15)
(15)
В силу известных формул

имеем:




 где
где 

Тогда с учетом того, что 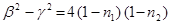 и
и  равенство (15) примет вид:
равенство (15) примет вид:
 (16)
(16)
Таким образом, в области D+ найдены частные решения уравнения (1), удовлетворяющие краевому условию (3):
 (17)
(17)
3. Построение частных решений в области гиперболичности. В уравнение (1) в области D- сделаем замену переменных 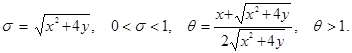 Тогда в координатах
Тогда в координатах  уравнение (1) примет вид:
уравнение (1) примет вид:

Разделив переменные  получим:
получим:
 (18)
(18)
 (19)
(19)
 (20)
(20)
 (21)
(21)
Решением уравнения (18), удовлетворяющего условиям (19), является функция
 (22)
(22)
Уравнение (20) так же, как и уравнение (12), является гипергеометрическим уравнением с аргументом  . Переходя к аргументу
. Переходя к аргументу  , построим его общее решение:
, построим его общее решение:
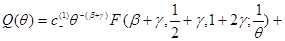
 (23)
(23)
Если  то функция (23) удовлетворяет граничным условиям (21). Тогда решением уравнения (20), удовлетворяющего условиям (21), будет:
то функция (23) удовлетворяет граничным условиям (21). Тогда решением уравнения (20), удовлетворяющего условиям (21), будет:
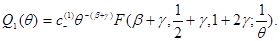
Таким образом, в области D- найдены частные решения уравнения (1), удовлетворяющие граничному условию (4):
 (24)
(24)
4. Построение собственных функций задачи Tl. Для нахождения собственных значений и собственных функций задачи Tl, построенную систему функций (17) и (24) удовлетворим условиям склеивания (2) и (5).
Из (17) и (24) вычислим:


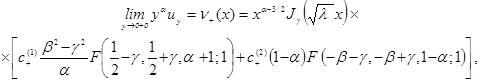

Приравнивая функции

получим систему

из которой находим коэффициенты  и
и  :
:
 (25)
(25)
Найденные значения  ,
, 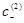 подставим в равенство (16) и решим его относительно g. Потребуем, чтобы
подставим в равенство (16) и решим его относительно g. Потребуем, чтобы  ,
,  . Тогда получим:
. Тогда получим:
 (27)
(27)
Поскольку  , то уравнение (27) имеет место, если
, то уравнение (27) имеет место, если 
Рассмотрим по отдельности случаи  и
и 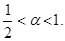
|
|
|
При  уравнение (27) имеет решения
уравнение (27) имеет решения  или
или  , где
, где  . С учетом того, что
. С учетом того, что 
 и
и  , решением (27) будет
, решением (27) будет

При  , решением (27) является
, решением (27) является  или
или  , где
, где  . С учетом тех же условий получим:
. С учетом тех же условий получим:

По формулам (25) и (26) находим  и
и 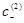 при найденных
при найденных  :
:

где

Из теории бесселевых функций известно [10], что при  функция
функция  имеет только вещественные нули. Тогда, обозначая через
имеет только вещественные нули. Тогда, обозначая через  --m-ый корень уравнения (11), находим собственные значения задачи Tl:
--m-ый корень уравнения (11), находим собственные значения задачи Tl:

Таким образом, построена система собственных функций задачи Tl:

Список литературы
Смирнов М.М. Уравнения смешанного типа. М., 1985.
Пономарев С.М. Спектральная теория основной краевой задачи для уравнения смешанного типа Лавретьева-Бицадзе. Автореферат диссертации … д-ра ф.-м. наук. М.: МГУ, 1981.
Моисеев Е.И. Уравнение смешанного типа со спектральным параметром. М.: МГУ, 1998.
Сабитов К.Б., Тихомиров В.В. О построении собственных значений и функций одной газодинамической задачи Франкеля // Математическое моделирование. 1990. Т. 2. № 10. С. 100-109.
Моисеев Е.И. о решении вырождающихся уравнений с помощью биортогональных рядов // Дифференц. уравнения. 1991. Т. 27. № 1. С. 94-103.
Мамедов Я.Н. О некоторых задачах на собственные значения для уравнения смешанного типа // Дифференц. уравнения. 1990. Т. 26. № 1. С. 163-168.
Сабитов К.Б., Вагапов В.З. О построении частных решений вырождающихся уравнений смешанного типа // Комплексный анализ, дифференц. уравнения и смежные вопросы: Тр. Международ. науч. конф. Уфа, 1996. С. 99-106
Вагапов В.З. построение частных решений одного уравнения смешанного типа // Тр. Всеросс. науч. конф. «Физика конденсированного состояния». Стерлитамак, 1997. Т. 1. С. 26-30.
Бейтмен Г., Эрдейи А. Высшие трансцендентные функции. М.: Наука, 1973.
Ватсон Г.Н. Теория бесселевых функций. 1. М., 1949.
Для подготовки данной работы были использованы материалы с сайта http://www.bashedu.ru
|
|
|


