Закон сохранения момента импульса

 

В подразделе 7.2 было введено понятие момента импульса произвольного тела и получено уравнение (7.6), описывающее изменение момента импульса под действием моментов сил. Если внешние силы не создают вращательного момента (М = 0), то уравнение (7.6) принимает вид, который выражает важный закон сохранения момента импульса:

dL = 0→L = const. (9.19)

Если суммарный момент внешних сил, действующих на тело, вращающееся вокруг оси, равняется нулю, то его момент импульса остается постоянным.

Этот закон применяется при рассмотрении вращения системы тел вокруг общей оси. Примеры, иллюстрирующие этот закон, представлены на рис. 9.19.

 

Рис. 9.19. Примеры проявления закона сохранения момента импульса: а) гимнаст, б) фигурист

 

Гимнаст, выполняющий сальто (рис. 9.19, а), в начальной фазе сгибает колени и прижимает их к груди, уменьшая тем самым момент инерции и увеличивая угловую скорость вращения вокруг горизонтальной оси. В конце прыжка его тело выпрямляется, момент инерции возрастает, угловая скорость уменьшается.

Фигурист, совершающий вращение вокруг вертикальной оси (рис. 9.19, б), в начале вращения приближает руки к корпусу, тем самым уменьшая момент инерции и увеличивая угловую скорость. Так, если момент инерции фигуриста уменьшается в два раза, то во столько же раз увеличивается его угловая скорость. В конце вращения происходит обратный процесс: при разведении рук увеличивается момент инерции и уменьшается угловая скорость, что позволяет легко остановиться.

Во время прыжка в воду с трамплина, толчок, испытываемый спортсменом в момент отрыва от гибкой доски, «закручивает» его, т. е. сообщает прыгуну начальный запас момента импульса относительно его ЦМ. Прежде чем прыгнуть в воду, прыгун совершает один или несколько оборотов с большой угловой скоростью; затем он вытягивает руки, увеличивая тем самым свой момент инерции и, следовательно, снижая свою угловую скорость до совсем небольшой величины перед входом в воду. Момент инерции при этом может измениться в 3,5 раза.

Глава 10 МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

Свободные колебания: гармонические и затухающие колебания

 

Внутри любого живого организма и в окружающей его среде непрерывно происходят разнообразные повторяющиеся процессы, например, работа сердца, движение маятника. Все эти явления подчиняются общим закономерностям, которые рассмотрим на примере механических колебаний.

Колебания — это движения или изменения состояния, обладающие той или иной степенью повторяемости.

Свободные колебания

 

Система из нескольких взаимодействующих тел, в которой могут происходить колебания, называется колебательной системой. Для колебательной системы характерно наличие состояния равновесия — такого взаимного расположение тел, которое при отсутствии внешнего воздействия может сохраняться сколь угодно долго. Для возбуждения колебаний необходимо вывести систему из равновесного состояния. Это можно сделать двумя способами:

• однократным внешним воздействием отклонить одно или несколько тел системы от равновесного положения;

• однократным внешним воздействием сообщить одному или нескольким телам системы начальные скорости.

Свободными механическими колебаниями называют колебательные движения системы, выведенной из положения равновесия вследствие начального смещения или сообщения начальной скорости.

Такие колебания совершаются при отсутствии внешнего воздействия за счет первоначально накопленной энергии. Свободные колебания возможны только в том случае, когда при отклонении тела от равновесного положения возникает сила, направленная в сторону положения равновесия. Такую силу называют возвращающей.

Пример

 

Колебательными движениями являются движения при свободных качаниях гимнаста в висе (вис — это положение тела, при котором гимнаст располагается плечами ниже опоры, удерживаясь руками или ногами) на перекладине. При движении его вниз момент силы тяжести относительно оси перекладины ускоряет движение. Во время движения вверх момент силы тяжести замедляет движение, так как действует ему навстречу.

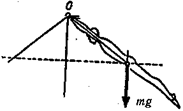
Рис. 10.1. Силы, изменяющие движение вокруг оси: при движении вниз сила тяжести ускоряет тело гимнаста, при движении вверх — замедляет

Гармонические колебания

 

Рассмотрим движение пружинного маятника — материальной точки массой т, подвешенной на пружине с жесткостью k. Если пружину оттянуть (сжать) на расстояние к от положения равновесия, то возникнет дополнительная упругая сила, величина и направление которой определяются законом Гука:

F = — k·x. (10.1)

Знак «—» показывает, что сила упругости всегда направлена в сторону, противоположную направлению смещения, т. е. к положению равновесия.

Предположим, что силы сопротивления отсутствуют. Тогда, подставив выражение (10.1) в формулу второго закона Ньютона, получим дифференциальное уравнение свободных колебаний при отсутствии трения:

 

 

Преобразуем выражение (10.2) следующим образом: Отношение положительно, поэтому целесообразно заменить его квадратом некоторой величины:

 

 

Получили дифференциальное уравнение второго порядка:

 

Его решение приводит к гармоническому закону:

где А — амплитуда колебаний,

ω₀ — собственная круговая (циклическая) частота колебаний,

φ= (φ₀t + φ₀) — фаза колебаний,

φ₀—начальная фаза колебаний (при t = 0).

Амплитуда и начальная фаза колебаний определяются начальными условиями движения, т. е. положением и скоростью материальной точки в момент времени t = 0.

Гармоническими колебаниями называются колебания, при которых наблюдаемая величина изменяется во времени по закону синуса или косинуса.

Таким образом, пружинный маятник совершает гармонические колебания.

График зависимости смещения от времени при гармонических колебаниях для случая φ₀ = 0 представлен на рис. 10.2.

Наряду с круговой частотой ω₀используют и другие характеристики колебательного движения:

• частота колебаний v, равная числу колебаний, совершаемых за единицу времени:

v= (10.6)

• период колебаний Т, равный времени, в течение которого совершается одно полное колебание:

 

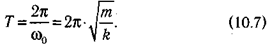
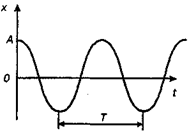
Рис. 10.2. График зависимости смещения от времени при гармонических колебаниях

 

Связь между указанными характеристиками определяется формулами:

Закон движения (10.5) позволяет определить скорость и ускорение колеблющегося тела в любой момент времени:

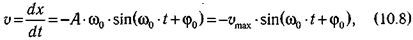
где v_max = А·ω₀ — максимальная скорость (амплитуда скорости);

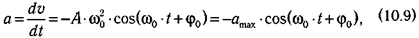
где а_mах = A∙ω₀²— максимальное ускорение (амплитуда ускорения).

Колеблющаяся материальная точка в любой момент времени обладает кинетической энергией собственного движения — Е_к и потенциальной энергией E _п, связанной с деформацией пружины.

Полная энергия колеблющегося тела складывается из его кинетической и потенциальной энергий:

 

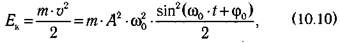
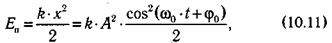
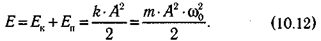
Как видно из (10.12), в этом случае полная механическая энергия системы не изменяется.

Затухающие колебания

 

Учет сил трения и сопротивления в реальных системах существенно изменяет характер движения: энергия движения постоянно убывает и колебания либо становятся затухающими, либо колебательное движение вообще не возникает.

Если в рассматриваемой системе появляются силы сопротивления среды (силы трения), то второй закон Ньютона можно записать так:

 

Предполагают, что при не очень больших амплитудах и частотах сила сопротивления пропорциональна скорости движения и, естественно, направлена противоположно ей:

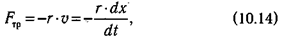
где r — коэффициент трения, характеризующий свойства среды оказывать сопротивление движению. Учитывая (10.13) и (10.14),

 

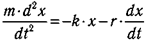
или

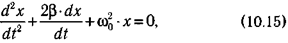
где

β─коэффициент затухания; ω₀ - круговая частота собственных колебаний системы.

Решение полученного дифференциального уравнения зависит от знака разности ω²= ω₀²— β², т. е. от соотношения между величинами β и ω₀. Параметр есть круговая частота затухающих колебаний.

а) Если ω₀²— β²> 0 и круговая частота со является действительной величиной, то решение уравнения (10.15) имеет вид:

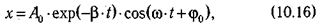
где ω = 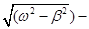круговая частота затухающих колебаний. График таких колебаний представлен на рис. 10.3.

Рис. 10.3. График зависимости смещения от времени при затухающих колебаниях (φ₀ -. 0)

В этом случае колебательный характер движения сохраняется, но амплитуда колебаний уменьшается со временем по экспоненциальному закону А = Α₀·ехр(— β · t). Круговая частота колебаний становится меньше, чем при отсутствии силы трения. Период затухающих колебаний в этом случае возрастает и определяется формулой, показывающей зависимость от коэффициента трения:

 

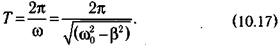
Быстрота убывания амплитуды колебаний зависит от коэффициента затухания: чем больше р, тем сильнее тормозящее действие среды и тем быстрее уменьшается амплитуда.

Количественно степень затухания характеризуется безразмерной величиной — логарифмическим декрементом затухания λ:

б) ω₀²< β² (сильное затухание), то колебательное движение не возникает. Период колебаний становится мнимой величиной. В этом случае запас механической энергии тела к моменту его возвращения в положение равновесия полностью или почти полностью расходуется на преодоление сил трения и тело останавливается. Такое движение называется апериодическим.

 

⇐ Предыдущая24252627282930313233Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: