 |
Примеры режимов сокращения
|
|
|
|
| Изометрический режим | Изотонический режим |
| Жевательные мышцы при сомкнутых челюстях (огромное напряжение) | Сокращение бицепса плеча |
| Сокращение миокарда желудочков при закрытых клапанах | Сокращение миокарда желудочков при открытии полулунных клапанов |
Уравнения Хилла
Между нагрузкой (Р) и скоростью укорочения мышцы (v) при изотоническом сокращении существует зависимость, выражаемая уравнением Хилла:
или
где а — постоянная, имеющая размерность силы; Ро — постоянная, соответствующая максимальной силе, развиваемой в изотоническом режиме (максимальный груз, который удерживает мышца без ее удлинения); b — константа, имеющая размерность скорости.
Анализ уравнения (11.7) показывает, что в зависимости от нагрузки Р поведение мышцы, т. е. ее сокращение, проявляется по-разному. Рассмотрим два крайних случая.
| Нагрузка | Скорость | Поведение мышцы |
| P=0 | 
| Максимальная скорость сокращения мышцы |
| P=P0 | v =0 | Сокращения мышцы не происходит |
Рассмотрим энергетические характеристики процесса. Работа А, совершаемая мышцей при одиночном укорочении на величину ∆ l, определяется известной формулой:
А = Р∙ ∆ l.
Эта зависимость очевидно нелинейная, так как скорость сокращения мышцы (v) зависит от нагрузки (Р). Но на ранней стадии сокращения этой нелинейностью можно пренебречь и считать v = const. Тогда
∆ l = v ∙∆ t,
аразвиваемая мышцей мощность 
имеет вид:
W=P∙v. (11.8)
Подставляя (11.7) в (11.8), получим зависимость полной мощности от развиваемой силы Р:
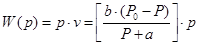(11.9)
График функции (11.9) имеет колоколообразную форму и представлен на рис. 11.22 в относительном виде.
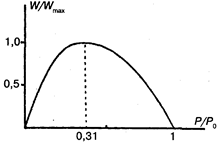
Рис. 11.22. Зависимость мощности мышцы от нагрузки
|
|
|
Эта кривая, полученная из уравнения Хилла, хорошо согласуется с опытными данными. В зависимости от нагрузки Р мощность имеет разные значения
| Мощность | Нагрузка |
| W=0 | Р=Р0 |
| W=0 | P=0 |
| W — максимальна |   ,
когда P=0,31P0
|
При работе мышц КПД при сокращении может быть определен как отношение совершенной работы к затраченной энергии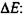 
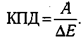
Развитие наибольшей мощности и эффективности сокращения достигается при усилиях 0,3—0,4 от максимальной изометрической нагрузки Р0 для данной мышцы. Это используют, например, спортсмены-велогонщики: при переходе с равнины на горный участок нагрузка на мышцы возрастает и спортсмен переключает скорость на низшую передачу, тем самым уменьшая Р, приближая ее к Ропт.
Практически КПД может достигать 40—60% для разных типов мышц.
Среднее значение плотности мышечной ткани 1050 кг/м3. Модуль Юнга Е =105 Па.
Сосудистая ткань
Механические свойства кровеносных сосудов определяются главным образом свойствами коллагена, эластина и гладких мышечных волокон. Содержание этих составляющих сосудистой ткани изменяется по ходу кровеносной системы. С удалением от сердца увеличивается доля гладких мышечных волокон, в артериолах они уже являются основной составляющей сосудистой ткани.
Так как стенки кровеносных сосудов построены из высокоэластического материала, то они способны к значительным обратимым изменениям размера при действии на них деформирующей силы. Деформирующая сила создается внутренним давлением. При заданном внутреннем давлении Р равновесное состояние сосуда описывается уравнением Ламе:
где r — внутренний радиус кровеносного сосуда, h — толщина стенки сосуда, σ — механическое напряжение в стенке сосуда.
Следует иметь в виду, что живой организм имеет два механизма сопротивления нагрузкам. Некоторые части организма (кости, зубы) воспринимают нагрузку так же, как и неживое тело. Другие (мышцы) — непрерывно подстраиваются под внешнюю нагрузку. Но сохранение напряжения в мышечной ткани требует непрерывного притока энергии. Расход энергии приводит к усталости мышц. Только обморок или смерть прерывают мышечные процессы.
|
|
|
Представления о механических свойствах биологических тканей важны для различных направлений:
• в спортивной и космической медицине;
• результативность спортивных достижений и ее возрастание побуждают спортивных медиков обращать внимание на физические возможности человека;
• в спортивной медицине следует знать устойчивость биологических структур по отношению к различным деформациям;
• в спортивной травматологии и ортопедии вопросы механического воздействия на организм являются определяющими.
|
|
|
