Контрольная работа: «Уравнение Шредингера. Одномерное движение».

Контрольная работа: «Соотношение неопределенностей. Операторы квантовой механики».

 

Вариант 1.

1. Полагая для электрона в атоме водорода, что неопределенность его расстояния от ядра сравнима с этим расстоянием, оценить минимально возможную энергию атома и соответствующее расстояние электрона от ядра.

2. Доказать эрмитовость оператора .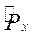

3. Найти: .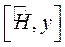

4. Найти собственные значения и нормированные собственные функции оператора .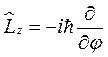

5. Определить возможные значения оператора 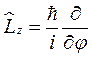и их вероятности для системы, находящейся в состоянии .

 

 

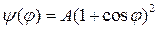Вариант 2.

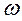1. Исходя из соотношения неопределенностей, показать, что минимально возможная энергия линейного гармонического осциллятора по порядку величины равна (где - собственная циклическая частота осциллятора).

2. Доказать эрмитовость оператора .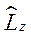

3. Найти: .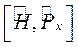

4. Найти собственные значения и нормированные собственные функции оператора .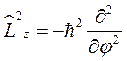

5. Определить собственные значения оператора 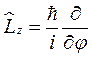и их вероятности для системы, находящейся в состоянии .

 

 

Контрольная работа: «Уравнение Шредингера. Одномерное движение».

 

Вариант 1.

1. Частица массы 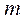падает слева на прямоугольный потенциальный барьер высотой . Энергия частицы равна Е, причем . Найти эффективную глубину Х_эф проникновения частицы под барьер, т.е. расстояние от границы барьера до точки, в которой плотность вероятности w нахождения частицы уменьшается в е раз. Показать, что при коэффициент отражения .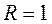

2. Частица массы 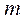находится в одномерной прямоугольной потенциальной яме шириной с бесконечно высокими стенками. Найти собственные значения энергии частицы и ее нормированные собственные функции.

3. Согласно теореме Эренфеста, средние значения квантовомеханических величин подчиняются законам классической механики. Доказать, что при движении частицы в потенциальном поле :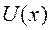

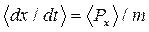
4. Плоским ротатором называют систему из двух жестко связанных частиц, вращающуюся в плоскости вокруг своего центра масс. Оператор энергии такого ротатора имеет вид 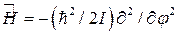, где I – момент инерции системы. Полагая, что в начальный момент волновая функция ротатора имеет вид , найти эту функцию в момент t.

 

Вариант 2.

1. Какие решения временного уравнения Шредингера называют стационарными? Показать, что такие решения получаются в том случае, когда 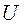не зависит от времени явного.

2. Частица массы 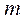падает на прямоугольный потенциальный барьер высотой . Энергия частицы равна Е, причем 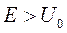. Найти коэффициент прозрачности D этого барьера.

3. Согласно теореме Эренфеста, средние значения квантовомеханических величин подчиняются законам классической механики. Доказать, что при движении частицы в потенциальном поле :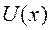

4. Плоским ротатором называют систему из двух жестко связанных частиц, вращающуюся в плоскости вокруг своего центра масс. Оператор энергии такого ротатора имеет вид 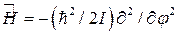, где I – момент инерции системы. Полагая, что в начальный момент волновая функция ротатора имеет вид 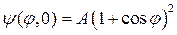, найти эту функцию в момент t.

 

Вариант 3.

1. Найти решение временного уравнения Шредингера для свободной частицы, движущейся с импульсом Р в положительном направлении оси Х.

2. Частица массы 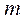движется слева направо в потенциальном поле, которое в точке х=0 испытывает скачок . Слева от точки х=0 энергия частицы равна Е. Найти коэффициент отражения R для случаев:

а) 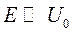; б) .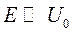

3. Частица находится в состоянии, описываемом собственной функцией 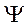оператора , который не зависит от времени явно. Показать, что соответствующее собственное значение А этого оператора будет сохраняться во времени, если оператор коммутирует с гамильтонианом .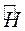

4. Плоским ротатором называют систему из двух жестко связанных частиц, вращающуюся в плоскости вокруг своего центра масс. Оператор энергии такого ротатора имеет вид 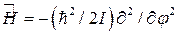, где I – момент инерции системы. Полагая, что в начальный момент волновая функция ротатора имеет вид 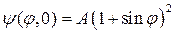, найти эту функцию в момент t.

 

Вариант 4.

1. Частица массы 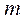находится в основном состоянии в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Максимальное значение плотности вероятности местонахождения частицы равно 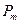. Найти ширину l ямы и энергию Е частицы в данном состоянии.

2. Частица массы 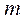падает на прямоугольный потенциальный барьер высотой . Энергия частицы равна Е, причем 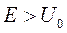. Найти коэффициент отражения R этого барьера.

3. Вычислив с помощью временного уравнения Шредингера производную по времени от среднего значения некоторой физической величины. А, изображаемой оператором , показать, что:

а) 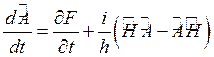б)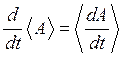

4. Плоским ротатором называют систему из двух жестко связанных частиц, вращающуюся в плоскости вокруг своего центра масс. Оператор энергии такого ротатора имеет вид 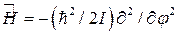, где I – момент инерции системы. Полагая, что в начальный момент волновая функция ротатора имеет вид , найти эту функцию в момент t.

Поделиться:

Воспользуйтесь поиском по сайту: