 |
Системы управления запасами
|
|
|
|
Вообще, система управления запасами – совокупность правил и показателей, определяющих момент времени и объем закупки продукции для пополнения запасов.
Параметры системы управления запасами:
- точка заказа – минимальный (контрольный) уровень запасов продукции, при наступлении которого необходимо их пополнение;
- нормативный уровень запасов – расчетная величина запасов, достигаемая при очередной закупки;
- объем отдельной закупки;
- частота совершения закупок – продолжительность интервала между двумя возможными закупками продукции, т.е. периодичность пополнения запасов продукции;
- пополняемое количество продукции, при котором достигается минимум затрат на хранение запаса при заданных затратах на пополнение и заданных альтернативных затратах инвестированного капитала.
При управлении запасами любого товара следует ответить на два вопроса: когда пополнять запас и каков должен быть размер заказа на пополнения. Для решения этих вопросов существуют определенные системы управления запасами:
- фиксированным размером заказа;
- с фиксированным интервалом между заказами (с постоянным уровнем запаса).
Остальные системы представляют собой разновидности этих двух систем.
Рассмотрим подробно систему с фиксированным размером запаса, которая проста и является своего рода классической. В этой системе размер заказа является постоянной величиной, и повторный заказ подается при уменьшении наличных запасов до определенного критического уровня точки заказа (рис.1.1.).
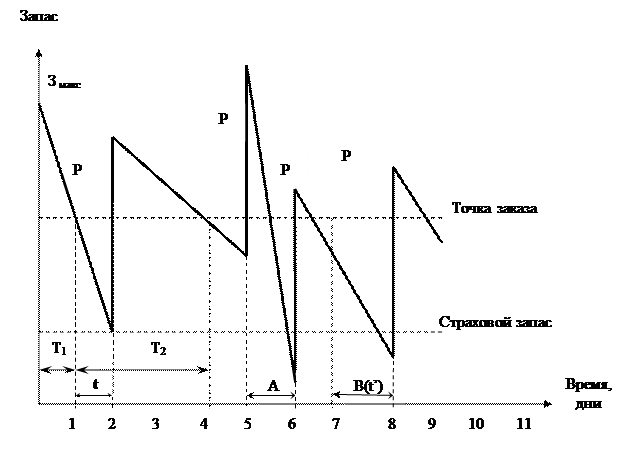
Рис.1.1. График движения запасов в системе управления запасами с фиксированным размером заказа.
Т1, Т2, …, Тi – величина отдельного i-го периода времени, через который повторяется заказ;
|
|
|
t – время, необходимое на размещение и выполнение заказа (в приведенном примере – 1 день);
Р – размер заказа, для данной системы контроля величина постоянная;
А – период непредвиденного усиления спроса;
В – период, в котором было допущено нарушение установленного срока поставки;
t' – фактический срок поставки в период В.
Эта система основана на выборе размера партии, минимизирующего общие издержки управления запасами. Последние состоят из издержек выполнения заказа и издержек хранения запасов.
Издержки выполнения заказа – это накладные расходы, связанные с реализацией заказа и зависящие от размера заказа. Если Со – издержки выполнения заказа, g – размер партии, то издержки выполнения заказа на единицу товара составят Со/g. Для определения годовых затрат выполнения заказа издержки выполнения заказа, приходящиеся на единицу товара, необходимо умножить на количество товара, реализованного за год, т.е. Со*S/g.
Издержки хранения запасов включают в себя расходы, связанные с физическим содержанием товаров на складе, и возможные проценты на капитал, вложенный в запас. Эти издержки выражаются в процентах от закупочной цены за определенное время. Если Си – закупочная цена единицы товара, i – издержки хранения, то Си*i – годовые издержки хранения товара. Издержки хранения определяются средним уровнем запасов. При постоянной интенсивности сбыта годовые издержки хранения запасов составляют Си·i·g/2.
Общие годовые издержки управления – это сумма годовых издержек выполнения заказов и годовых издержек хранения запасов, т.е. С = (Со·S/g + Си·i·g/2).
Оптимальный размер партии можно определить исходя из общих годовых издержек по формуле Уилсона:
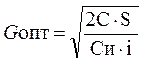
Точку заказа в этом случае можно определить по формуле:
Р = В + Sd·L,
где Sd – средний суточный сбыт.
Средний уровень запасов для этой модели составит:
|
|
|
Jср = В + Q/2,
где Q – размер запаса.
Система управления запасами с фиксированным размером заказа используется при значительных издержках управления запасами, и если поставщик налагает ограничения на минимальный размер партии поставки.
Рассмотренная система управления запасами функционирует в идеальных условиях, т.е. предполагается постоянный темп потребления, нулевой запас в точке пополнения запасов и мгновенных характер самого процесса пополнения запаса.
В условиях дефицита оптимальный размер заказа определяется:
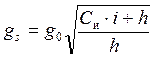
где h – издержки, обусловленные дефицитом.
Максимальный положительный запас:
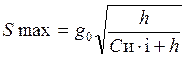
Теперь рассмотрим систему с фиксированным интервалом между заказами. В этой системе издержки управления запасами в явном виде не рассматриваются и фиксированный размер заказа отсутствует. Через постоянные промежутки времени проводится проверка состояния запасов, и если после предыдущей проверки было реализовано какое-либо количество товаров, то подается заказ. Размер заказа зависит от размера сбыта после последней проверки. Размер заказа равен разности между максимальным уровнем М, до которого происходит пополнение запасов, и фактическим уровнем в момент проверки Jф, т.е. g = M – Jф.
Максимальный уровень запасов определяется по формуле:
М = В + Sd (L + R),
где R – длительность промежутка времени между проверками.
Средний уровень запасов составляет:
Jср = В + 1/2 Sd R
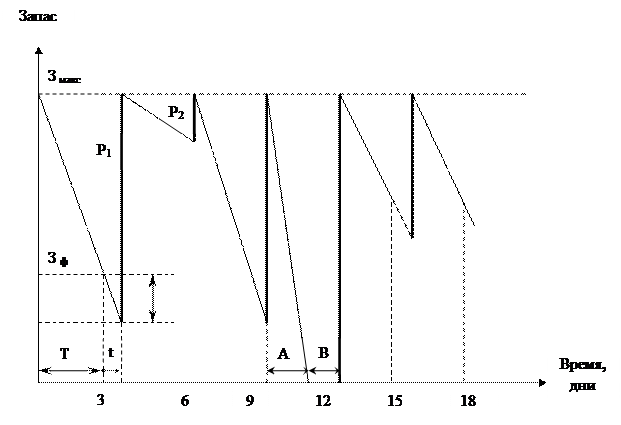
Рис.1.2. График движения запасов в системе управления запасами с фиксированным интервалом времени между заказами
Т – интервал времени, через который повторяется заказ (в нашем случае – 3 дня) – для данной системы величина постоянная;
t – время, необходимое на размещение и выполнение заказа (в приведенном примере – 1 день);
Р1, Р2, …, Рi – величина отдельного, i-го заказа;
З макс – предусмотренный нормой максимальный запас;
З ф – фактический запас на момент проверки;
З t – запас, расходуемый за время t, необходимое для размещения и выполнение заказа;
А – период времени с интенсивным спросом;
В – период времени с нулевым запасом.
Рассмотренные системы не являются единственно возможными. Выбор той или иной системы зависит от следующих обстоятельств:
|
|
|
1. Если издержки управления запасами значительные и их можно вычислить, то следует применять систему с фиксированным размером заказа.
2. Если издержки управления запасами незначительные, то более предпочтительной оказывается система с постоянным уровнем запасов.
3. При заказе товаров поставщик налагает ограничения на минимальный размер партии. В этом случае желательно использовать систему с фиксированным размером заказа, поскольку легче один раз скорректировать фиксированный размер партии, чем непрерывно регулировать его переменный заказ.
4. Однако, если налагаются ограничения, связанные с грузоподъемностью транспортных средств, то более предпочтительной является система с постоянным уровнем запасов.
5. Система с постоянным уровнем запасов более предпочтительна и в том случае, когда поставка товаров происходит в установленные сроки.
Система с постоянным уровнем часто выбирается тогда, когда необходимо быстро реагировать на изменение сбыта.
Практическая часть
Исходные данные:
Цена материала составляет 131 рубль за килограмм. Доставка партии материалов грузовым автомобилем обходится предприятию в 1430 рублей. На каждый рубль, вложенный в запас материала приходится 0,025 рубля издержек хранения в неделю.
Издержки, вызванные отсутствием одного килограмма материала в неделю, составляют 15797 руб./ кг×нед. Данные об интенсивности расходования материала понедельно в течение 2009 года представлены в таблице 1.
Таблица 2.1.
Интенсивность расходования материала понедельно в течение 2009 г.
| № недели | D, кг/нед | № недели | D, кг/нед | № недели | D, кг/нед |
| 15,8 | 56,9 | ||||
| 32,7 | 52,6 | 53,2 | |||
| 45,3 | 71,2 | 64,6 | |||
| 48,9 | 45,3 | 68,9 | |||
| 52,1 | 61,2 | 54,2 | |||
| 41,3 | 35,8 | 43,1 | |||
| 60,3 | 45,3 | 55,8 | |||
| 75,4 | 53,7 | 59,7 | |||
| 43,6 | 64,1 | 38,2 | |||
| 33,4 | 52,9 | 56,2 | |||
| 44,8 | 63,1 | 64,8 | |||
| 52,1 | 42,8 | 70,3 | |||
| 62,8 | 39,1 | 62,1 | |||
| 61,4 | 45,8 | 39,2 | |||
| 52,3 | 63,4 | 45,8 | |||
| 66,7 | 52,5 | 31,7 | |||
| 63,8 | 41,6 | ||||
| 10,3 | 45,5 |
|
|
|
Данные об объеме израсходованного за неделю материала систематизируем в возрастающем порядке от D1 до DN, где Di-1£ Di £ Di+1.
Таблица 2.2.
Интенсивность расходования материала понедельно в течение 2009 г. в возрастающем порядке
| № недели | D, кг/нед | № недели | D, кг/нед | № недели | D, кг/нед |
| 45,3 | 60,3 | ||||
| 10,3 | 45,5 | 61,2 | |||
| 15,8 | 45,8 | 61,4 | |||
| 31,7 | 45,8 | 62,1 | |||
| 32,7 | 48,9 | 62,8 | |||
| 33,4 | 52,1 | 63,1 | |||
| 35,8 | 52,1 | 63,4 | |||
| 38,2 | 52,3 | 63,8 | |||
| 39,1 | 52,5 | 64,1 | |||
| 39,2 | 52,6 | 64,6 | |||
| 41,3 | 52,9 | 64,8 | |||
| 41,6 | 53,2 | 66,7 | |||
| 42,8 | 53,7 | 68,9 | |||
| 43,1 | 54,2 | 70,3 | |||
| 43,6 | 55,8 | 71,2 | |||
| 44,8 | 56,2 | 75,4 | |||
| 45,3 | 56,9 | ||||
| 45,3 | 59,7 |
Затем весь интервал имеющихся значений разбиваем на М=10 равных интервалов длиной:
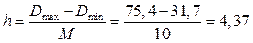 , где:
, где:
Dmax – максимальное значение спроса на товар за рассмотренный период;
Dmin – минимальное значение спроса на товар за тот же период.
После этого находим середины всех частичных интервалов по формуле (табл. 3):
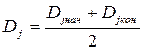 , где:
, где:
Djнач, Djкон- соответственно начало и конец j-го интервала.
Таблица 2.3.
Расчет отдельных параметров.
| № интервала, j | Значение интервала | Середина интервала D'j, кг/нед | Кол-во значений D'j, попавших в j-ый интервал, fj | D'j·fj |
(D'j– 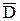 )²·fj )²·fj
|
| 31,7-36,07 | 33,885 | 135,54 | 1403,102 | ||
| 36,07-40,44 | 38,255 | 114,765 | 618,543 | ||
| 40,44-44,81 | 42,625 | 255,75 | 598,681 | ||
| 44,81-49,18 | 46,995 | 328,965 | 221,012 | ||
| 49,18-53,55 | 51,365 | 359,555 | 10,920 | ||
| 53,55-57,92 | 55,735 | 278,675 | 48,703 | ||
| 57,92-62,29 | 60,105 | 300,525 | 280,575 | ||
| 62,29-66,66 | 64,475 | 451,325 | 984,783 | ||
| 66,66-71,03 | 68,845 | 206,535 | 790,336 | ||
| 71,03-75,4 | 73,215 | 146,43 | 848,802 | ||
| Сумма | - | 2578,065 | 5805,458 |
Произведем оценку математического ожидания, дисперсии и среднеквадратического отклонения распределения вероятностей интенсивности расходования материала. Эти параметры оцениваются при помощи следующих формул:
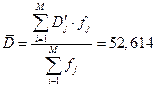
Вывод: средняя интенсивность расходования материала в неделю составляет 52,614 кг/нед.

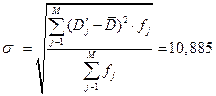
Вывод: на 10,885 кг в среднем интенсивность расходования материала за неделю может отклониться от ее среднего значения.
Сделаем предположение о характере распределения вероятностей. В частности, если │D'j – 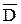 │< 3·σ для всех значений D'j, то можно предположить, что интенсивность расходования товара является нормально распределенной непрерывной случайной величиной. В случае если
│< 3·σ для всех значений D'j, то можно предположить, что интенсивность расходования товара является нормально распределенной непрерывной случайной величиной. В случае если 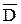 ≈σ, то можно сделать предположение о показательном распределении интенсивности расходования товара. Если же каждое значение D'j встречается с одинаковой частотой, предполагается равномерное распределение вероятностей.
≈σ, то можно сделать предположение о показательном распределении интенсивности расходования товара. Если же каждое значение D'j встречается с одинаковой частотой, предполагается равномерное распределение вероятностей.
|
|
|
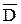 = 52,614
= 52,614
σ = 10,885
Т.к. условие 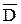 ≈σ не выполняется, и каждое значение D'j не встречается с одинаковой частотой, то распределение не является показательным и равномерным. Для подтверждения того, что распределение вероятностей в данном случае является нормальным, проверим выполнения следующего условия:
≈σ не выполняется, и каждое значение D'j не встречается с одинаковой частотой, то распределение не является показательным и равномерным. Для подтверждения того, что распределение вероятностей в данном случае является нормальным, проверим выполнения следующего условия:
│D'j – 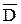 │< 3·σ
│< 3·σ
1) D'1 = 33,885;
│33,885 – 52,614│< 3*10,885
│18,729│< 32,655
2) D'2 = 38,255; │14,359│< 32,655
3) D'3 = 42,625; │9,989│< 32,655
4) D'4 = 46,995; │5,619│< 32,655
5) D'5 = 51,365; │1,249│< 32,655
6) D'6 = 55,735; │3,121│< 32,655
7) D'7 = 60,105; │7,491│< 32,655
8) D'8 = 64,475; │11,861│< 32,655
9) D'9 = 68,845; │16,231│< 32,655
10) D'10 = 73,215; │20,601│< 32,655
Для проверки правильности сделанного предположения о характере распределения рассчитываем выравнивающие частоты значений D'j по формуле:
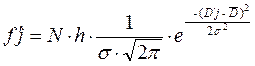
1) f'1 = 49·4,37· 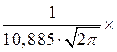
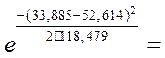 1,786
1,786
2) f'2 = 3,288
3) f'3 = 5,151
4) f'4 = 6,869
5) f'5 = 7,797
6) f'6 = 7,532
7) f'7 = 6,193
8) f'8 = 4,334
9) f'9 = 2,582
10)f'10 = 1,309
Таблица 2.4.
Расчет реальных (fj) и выравнивающих частот (f'j)
| D'j, кг/нед | fj | f 'j | (fj – f 'j)²/f 'j |
| 33,885 | |||
| 38,255 | |||
| 42,625 | 0,2 | ||
| 46,995 | |||
| 51,365 | 0,125 | ||
| 55,735 | 1,125 | ||
| 60,105 | 0,167 | ||
| 64,475 | 2,25 | ||
| 68,845 | |||
| 73,215 | |||
| Сумма | 6,867 |
Также для проверки гипотезы о характере распределения используется критерий Пирсона. Согласно критерию Пирсона, если случайная величина подчиняется нормальному распределению, то следующее неравенство выполняется с вероятностью 1 – β:
 , где:
, где:
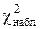 - наблюдаемое значение c2;
- наблюдаемое значение c2;
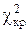 (b, k) - критическое значение c2.
(b, k) - критическое значение c2.
1 – β = 1 – 0,01 = 0,95
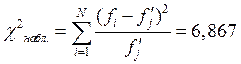
k = М – 1 – Z = 10 – 1 – 2 = 7,
где Z – число параметров, которыми определяется предполагаемое распределение. Т.к. распределение нормальное, то Z = 2 (данное распределение определяется двумя параметрами: математическое ожидание и среднеквадратическое отклонение).
При вероятности 0,95 и числе степеней свободы 7 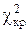 = 14,067. Таким образом, наблюдаемое значение критерия Пирсона не превышает критическое значение, т.е. проведенный расчет дает право не отвергать гипотезу о нормальном характере распределения.
= 14,067. Таким образом, наблюдаемое значение критерия Пирсона не превышает критическое значение, т.е. проведенный расчет дает право не отвергать гипотезу о нормальном характере распределения.
Построим график распределения реальных (fj) и выравнивающих (теоретических) частот (f'j) в одной системе координат.
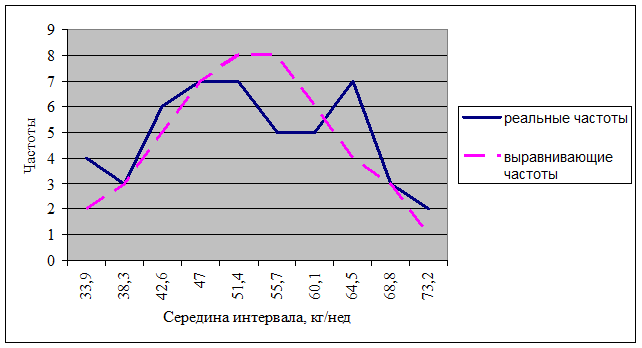
Рис.2.1. Распределение реальных и выравнивающих частот
Определим оптимальный уровень текущего запаса в момент поставки пополнения по формуле:
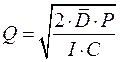 , где:
, где:
Р – затраты на доставку;
I – коэффициент, показывающий сколько рублей издержек содержания приходится на каждый рубль, вложенный в запас товара;
С – цена запасаемого товара.
Р = 1430 руб.
I = 0,025 руб.
С = 131 руб./кг.
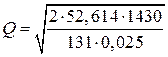 = 214,352 кг.
= 214,352 кг.
Оптимальную периодичность поставок рассчитываем по формуле:
Тц = 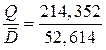 = 4,074 нед.
= 4,074 нед.
Затем определяем, с какой вероятностью α необходимо обеспечить отсутствие дефицита товара:
 , где:
, где:
g – издержки, связанные с дефицитом запасаемого товара в единицу времени.
G = 15797 руб./ кг×нед.

Далее определяем размер страхового запаса S. Т.к. спрос на товар подчиняется нормальному распределению, то для нахождения страхового запаса используется следующее уравнение:
 , где:
, где:
S – размер страховой составляющей партии.
Для нахождения значения S можно воспользоваться таблицами значений функции Лапласа 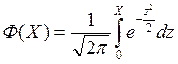 . В этом случае исходное уравнение преобразуется к виду:
. В этом случае исходное уравнение преобразуется к виду:
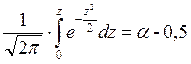
где 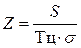 .
.

C помощью таблиц значений функции Лапласа из данного уравнения находим z = 3,6, а затем размер страхового запаса по формуле:
S = z · Tц · σ = 3,6*4,074*10,885 = 159,644
Нарисуем схему пополнения и расходования запаса товара.
Запасы, шт.
 |
Q + S 
 S
S

4,074 8,148 12,222 16,296 20,37 24,444 t, нед.
Рис.2.2. Схема пополнения и расходования запасов товара
Для эффективного управления запасами составим инструкцию по контролю за состоянием системы управления запасом товара. Инструкция предназначена для работников, ведущих учет, контроль и управление запасами. Данная инструкция предполагает выполнение следующих шагов:
1) определить, какой уровень запасов необходимо иметь для обеспечения обслуживания потребителя;
2) решить, как часто будут пополняться запас товара, т.е. определить цикл заказа;
3) четко соблюдать сроки поставки;
4) рассмотреть возможность появления сбоев в потреблении запасов;
5) построить графики движения запасов, иллюстрирующие все возможные ситуации;
6) определить издержки, связанные с созданием и хранением запасов.
Заключение
В ходе курсовой работы были решены все задачи, поставленные в начале работы. В результате чего можно сделать следующие выводы. Запас – это форма существования материального потока. Запасы служат для того, чтобы ослабить непроизводственные зависимости между поставщиком, производителем и потребителем. Например, запасы сырья ослабляют зависимость между поставщиком и производителем продукции, запасы готовой продукции ослабевают зависимость между производителем этой продукции и потребителем, а запасы полуфабрикатов, находящихся в процессе производства, снижают зависимость друг от друга отдельных цехов.
В курсовой работе выделены две основные логистические системы управления запасами: система с фиксированным размером заказа и система с фиксированным интервалом времени между заказами. Одна и другая системы проектируются с целью непрерывного обеспечения потребителя каким-либо видом материальных ресурсов. Системы с фиксированным размеромхарактеризуется тем, что уровень запасов постоянно контролируется. Когда количество падает ниже установленного уровня, выдаётся заказ на восполнение запасов. Заказывается всегда одно и то же количество. Системы с фиксированным временем – это системы, в которых заказы на восполнение размещаются с заданной периодичностью, например, раз в две недели. Заказываемое количество непостоянно и зависит от имеющегося остатка.
Список литературы
1) Логистика: Учебник/Под ред. Б.А. Аникина: 2-е изд., перераб. и доп. – М.: ИНФРА-М, 2001.
2) Нерум Ю.М. Логистика: Учебник для вузов. – 2-е изд., перераб. и доп. – М.: ЮНИТИ-ДАНА, 2000.
3) Гаджинский А.М. Логистика: Учебник для высших и средних специальных учебных заведений. – 7-е изд., перераб. и доп. – М.: Издательско-торговая корпорация «Дашков и К», 2003.
4) Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учебник. – М.: ИНФРА-М, 1997.
|
|
|


