Матрица применения способов детерминированного факторного анализа

Способы	Факторные модели
Мультипликативные	Аддитивные	Кратные	Смешанные
Цепной подстановки	+	+	+	+
Абсолютных разниц	+	-	+	-
Относительных разниц	+	-	-	у = а ∙ (b−с)
Интегральный	+	-	+	у = a/∑bi

Обозначения: + используется; – не используется

Различают четыре типа детерминированных моделей:

Аддитивныемодели представляют собой алгебраическую сумму показателей и имеют вид:

Мультипликативные − это последовательное расчленение факторов исходной системы на факторы-сомножители. Модели в обобщенном виде могут быть представлены формулой:

Кратные модели: y = x₁ / x₂.

Смешанные модели представляют собой комбинацию перечисленных выше моделей и могут быть описаны с помощью специальных выражений:

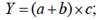
1. Наиболее универсальным из способов детерминированного анализа является способ цепной подстановки.

Он используется для расчета влияния факторов во всех типах детерминированных факторных моделей: аддитивных, мультипликативных, кратных и смешанных (комбинированных). Данный способ основан на элиминировании.

Элиминирование — это процесс поэтапного исключения воздействия всех факторов на величину результативного показателя, кроме одного. При этом исходя из того, что все факторы изменяются независимо друг от друга, т.е. сначала изменяется один фактор, а все остальные остаются без изменения. Потом изменяются два при неизменности остальных и т.д.

Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя. Сущность этого приема состоит в том, чтобы из всех действующих факторов выделить основные, имеющие решающее влияние на изменение показателя. С этой целью определяют ряд условных значений результативного показателя, которые учитывают изменение одного, затем двух, трех и последующих факторов, допуская, что остальные не меняются. Это означает, что в расчетах последовательно заменяют частные плановые показатели отчетными, полученные результаты сравнивают с имеющимися предыдущими данными. Сравнение значений результативного показателя до и после изменения уровня того или другого фактора позволяет элиминировать влияние всех факторов, кроме одного, и определить воздействие последнего на прирост результативного показателя.

При использовании способа цепных подстановок большое значение имеет последовательность подстановок:в первую очередь нужно учитывать изменение количественных, а затем качественных показателей. Применение обратной последовательности расчетов не дает правильной характеристики влияния факторов.

Таким образом, применение способа цепной подстановки требует знания взаимосвязи факторов, их соподчиненности, умения правильно их классифицировать и систематизировать.

В общем виде применение способа цепных постановок можно описать следующим образом:

y₀ = a₀ ∙ b₀ ∙ c₀;

y_a = a₁ ∙ b₀ ∙ c₀;

y_b = a₁ ∙ b₁ ∙ c₀;

y₁ = a₁ ∙ b₁ ∙ c₁;

где a₀, b₀, c₀- базисные значения факторов, оказывающих влияние на обобщающий показатель у;

a₁, b₁, c₁- фактические значения факторов;

y_a, y_b, - промежуточные значения результирующего показателя, связанного с изменением факторов а и b,соответственно.

Общее изменение Δу = у₁ – у₀ складывается из суммы изменений результирующего показателя за счет изменения каждого фактора при фиксированных значениях остальных факторов. Т.е. сумма влияния отдельных факторов должна равняться общему приросту результативного показателя.

∆y = ∆y_a + ∆y_b + ∆y_c = y₁– y₀

∆y_a = y_a – y₀;

∆y_b = y_b – y_a;

∆y_c = y₁ – y_b.

Преимущества данного способа: универсальность применения, простота расчетов.

Недостаток метода состоит в том, что, в зависимости от выбранного порядка замены факторов, результаты факторного разложения имеют разные значения.

 

2. Способ абсолютных разниц является модификацией способа цепной подстановки.

Способ абсолютных разниц применяется для расчета влияния факторов на прирост результативного показателя в детерминиро­ванном анализе, но только в мультипликативных моделях (Y = х₁ ∙ х₂ ∙ х₃ ∙∙∙∙∙ х_n) и моделях мультипликативно-аддитивного типа: Y = (а - b)∙с и Y = а∙(b - с). И хотя его использование ограничено, но благодаря своей простоте он получил широкое применение в АХД.

Суть метода способа − величина влияния факторов рассчиты­вается пу­тем умножения абсолютного прироста значения исследуемого фактора на базовую (плановую) величину факторов, которые на­ходятся справа от него, и на фактическую величину факторов, рас­положенных в модели слева от него.

y₀ = a₀ ∙ b₀ ∙ c₀

∆y_a = ∆a ∙ b₀ ∙ c₀

∆y_b = a₁ ∙ ∆b ∙ c₀

∆y_с = a₁ ∙ b₁ ∙ ∆с

y₁ = a₁ ∙ b₁ ∙ c₁

Алгебраическая сум­ма прироста результативного показателя за счет отдельных факто­ров должна равняться его общему изменению Δу = у₁ – у₀.

∆y = ∆y_a + ∆y_b + ∆y_c = у₁ – у₀

 

3. Способ относительных разниц Он используется в случаях, когда ис­ходные данные содержат определенные ранее относительные отклонения факторных показателей в процентах. Применяется для измерения влияния факторов на прирост результативного показателя только в мультипликативных моделях. Здесь используются относитель­ные приросты факторных показателей, выраженные в виде коэф­фициентов или процентов. Рассмотрим методику расчета влияния факторов этим способом для мультипликативных моделей типа Y = abc.

Изменение результативного показателя определяется следу­ющим образом:

Согласно данному алгоритму для расчета влияния первого фак­тора необходимо базовую величину результативного показателя умножить па относительный прирост первого фактора, выражен­ного в виде десятичной дроби. Чтобы рассчитать влияние второго фактора, нужно к базовой величине результативного показателя прибавить изменение его за счет первого фактора и затем полученную сумму умножить на от­носительный прирост второго фактора. Влияние третьего фактора определяется аналогично: к базовой величине результативного показателя необходимо прибавить его прирост за счет первого и второго факторов и полученную сумму умножить на относительный прирост третьего фактора и т.д.

Результаты расчетов такие же, как и при использо­вании предыдущих способов.

Способ относительных разниц удобно применять в тех случаях, когда требуется рассчитывать влияние большого комплекса факто­ров (8-10 и более). В отличие от предыдущих способов здесь значи­тельно сокращается число вычислительных процедур, что обуслов­ливает его преимущество.

 

4. Интегральный метод оценки факторных влияний позволяет избежать недостатков, присущих методу цепной подстановки, и не требует применения приемов по распределению неразложимого остатка по факторам. Интегральный метод позволяет достигнуть полного разложения результативного показателя по факторам и носит универсальный характер, т.е. применим к мультипликативным, кратным и смешанным моделям.

Рассмотрим алгоритмы расчетов влияния факторов для разных моделей:

1) Модель вида: y = a ∙ b

2) Модель вида: y = a ∙ b ∙ с

3) Модель вида:

 

3) Модель вида:

Результаты расчетов по интегральному методу существенно отличаются от того, что дает метод цепных подстановок или модификации последнего. Чем больше величина изменений факторов, тем разница значительнее.

 

5. Индексный метод позволяет выявить влияние на изучаемый совокупный показатель различных факторов. Основывается на относительных показателях динамики, выражающих отношение уровня анализируемого показателя в отчетном периоде к его уровню в базисном периоде.

Всякий индекс исчисляется сопоставлением соизмеряемой (отчетной) величины с базисной. Индексы, выражающие соотношение непосредственно соизмеряемых величин, называются индивидуальными, а характеризующие соотношения сложных явлений — групповыми, или тотальными. Статистика называет несколько форм индексов, которые используются в аналитической работе − агрегатная, арифметическая, гармоническая и др.

6. Спо­соб пропорционального деления может быть использован в ряде случаев для определения величины влияния факторов на прирост результативного показателя. Это касается тех случаев, когда мы имеем дело с аддитивными моделями Y=∑х_i и моделями кратно-аддитивного типа:

В первом случае, когда имеем одноуровневую модель типа Y= а + b + с, расчет проводится следующим образом:

В моделях кратно-аддитивного типа сначала необходимо спосо­бом цепной подстановки определить, насколько изменился результативный показатель за счет числителя и знаменателя, а затем про­извести расчет влияния факторов второго порядка способом пропорционального деления по вышеприведенным алгоритмам.

7. Для решения такого типа задач можно использовать также спо­соб долевого участия. Для этого сначала определяется доля каждо­го фактора в общей сумме их приростов (коэффици­ент долевого участия), которая затем умножает­ся на общий прирост результативного показателя (табл. 4.2):

Применительно к классу детерминированных факторных кратных систем используются следующие основные приемы моделирования:

1) метод удлинения исходной факторной системы заключается в разложении числителя кратной модели на составляющие его факторы с последующим получением развитой факторной модели аддитивного вида;

2) метод формального разложения исходной факторной системы заключается в разложении знаменателя исходной факторной системы кратного вида на составляющие его факторы с получением конечной факторной системы комбинированного вида;

3) метод расширения исходной факторной системы предполагает умножение и числителя, и знаменателя кратной модели на один и тот же экономический показатель с последующим получением конечной факторной системы мультипликативного вида;

4) метод сокращения исходной факторной системы и числитель, и знаменатель исходной факторной модели делятся на один и тот же экономический показатель с получением развитой факторной системы того же кратного вида, но с другим составом факторов.

Примеры апробации вышерассмотренных методов моделирования детерминированных факторных систем рассмотрены нами в табл. 2.

Поделиться:

Воспользуйтесь поиском по сайту: