 |
I. Шифры одинарной перестановки.
|
|
|
|
РТУ МИРЭА
Кафедра КБ-1 «Защита информации»
ПРАКТИЧЕСКАЯ РАБОТА № 2
по дисциплине «Криптографические методы защиты информации»
(шифр и наименование учебной дисциплины)
ТЕМА Шифр перестановки
(наименование темы лабораторного занятия)
РТУ МИРЭА – 2018 г.
ПРАКТИЧЕСКАЯ РАБОТА № 2.
ШИФРЫ ПЕРЕСТАНОВКИ
Все шифры перестановки делятся на два подкласса:
- шифры одинарной (простой) перестановки. При шифровании символы перемещаются с исходных позиций в новые один раз;
- шифры множественной (сложной) перестановки. При шифровании символы перемещаются с исходных позиций в новые несколько раз.
I. Шифры одинарной перестановки.
В общем случае для данного класса шифров при шифровании и дешифровании используется таблица перестановок.

Рис.1. Таблица перестановок
В первой строке данной таблицы указывается позиция символа в исходном сообщении, а во второй – его позиция в шифрограмме. Таким образом, максимальное количество ключей для шифров перестановки равно n! где n – длина сообщения.
Шифр простой одинарной перестановки. Для шифрования и дешифрования используется таблица перестановок, аналогичная показанной на рис.2.

Рис.2. Таблица перестановок
Например, если для шифрования исходного сообщения «АБРАМОВ» использовать таблицу, представленную на рис.2, то шифрограммой будет «РАВБОМА». Для использования на практике такой шифр не удобен, так как при больших значениях n приходится работать с длинными таблицами и для сообщений разной длины необходимо иметь свою таблицу перестановок.
Шифр блочной одинарной перестановки. При использовании этого шифра задается таблица перестановки блока символов, которая последовательно применяется до тех пор, пока исходное сообщение не закончится. Если исходное сообщение не кратно размеру блока, тогда оно при шифровании дополняется произвольными символами.
|
|
|

Рис.3. Таблица перестановок
Для примера выберем размер блока, равный 3, и примем таблицу перестановок, показанную на рис.3. Дополним исходное сообщение «АБРАМОВ» буквами Ь и Э, чтобы его длина была кратна 3. В результате шифрования получим «РАБОАМЭВЬ».
Количество ключей для данного шифра при фиксированном размере блока равно m!, где m – размер блока.
Шифры маршрутной перестановки. Широкое распространение получили шифры перестановки, использующие некоторую геометрическую фигуру (плоскую или объемную). Преобразования состоят в том, что в фигуру исходный текст вписывается по ходу одного маршрута, а выписывается по-другому. Один из таких шифров – шифр «Сцитала» - упоминался ранее. Некоторые из них приводятся ниже.
Шифр табличной маршрутной перестановки. Наибольшее распространение получили шифры маршрутной перестановки, основанные на таблицах. При шифровании в такую таблицу вписывают исходное сообщение по определенному маршруту, а выписывают (получают шифрограмму) - по-другому. Для данного шифра маршруты вписывания и выписывания, а также размеры таблицы являются ключом.

Рис.4. Пример использования шифра маршрутной перестановки
Например, исходное сообщения «АБРАМОВ ИЛЬЯ СЕРГЕЕВИЧ» вписывается в прямоугольную таблицу размерами 4х6, маршрут вписывания – слева-направо сверху-вниз, маршрут выписывания – сверху-вниз слева-направо. Шифрограмма в этом случае выглядит «АВ_ЕБ_СВРИЕИАЛР ЧМЬГ_ОЯЕ_».
Шифр вертикальной перестановки. Является разновидностью предыдущего шифра. К особенностям шифра можно отнести следующие:
- количество столбцов в таблице фиксируется и определяется длиной ключа;
- маршрут вписывания строго соответствует маршруту, показанному на рис.4;
|
|
|
- шифрограмма выписывается по столбцам в соответствии с их нумерацией (ключом).
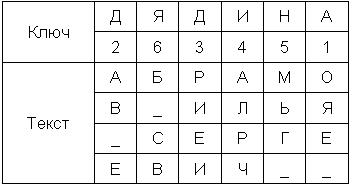
Рис.5. Пример использования шифра вертикальной перестановки
В качестве ключа можно использовать слово или фразу. Тогда порядок выписывания столбцов соответствует алфавитному порядку букв в ключе. Например, если ключевым словом будет «ДЯДИНА», то присутствующая в нем буква А получает номер 1, Д – 2 и т.д. Если какая-то буква входит в слово несколько раз, то ее появления нумеруются последовательно слева направо. В примере первая буква Д получает номер 2, вторая Д – 3.
При шифровании сообщения «АБРАМОВ ИЛЬЯ СЕРГЕЕВИЧ» результат будет «ОЯЕ_АВ_ЕРИЕИАЛРЧМЬГ_Б_СВ».
Шифр «Поворотная решетка». В 1550 году итальянский математик Джироламо Кардано, состоящий на службе у папы Римского, в книге «О тонкостях» предложил новую технику шифрования - решётку Кардано. Ее считают первым транспозиционным шифром, или, как ещё называют, геометрическим шифром, основанным на положении букв в шифртексте.
Для шифрования и дешифрования изготовляется прямоугольный трафарет с четным количеством строк и столбцов. В трафарете вырезаются клетки таким образом, чтобы при наложении его на таблицу того же размера четырьмя возможными способами, его вырезы полностью покрывали все ячейки таблицы ровно по одному разу.
При шифровании трафарет накладывается на таблицу. В видимые ячейки таблицы выписываются буквы исходного текста слева-направо сверху-вниз. Далее трафарет поворачивается и вписывается следующая часть букв. Эта операция повторяется еще два раза. Шифрограмму выписывают из итоговой таблицы по определенному маршруту.
Таким образом, ключом при шифровании является трафарет, порядок его поворотов и маршрут выписывания.
Пример шифрования сообщения «АБРАМОВ+ДЯДИНА» показан на рис.6. Результат шифрования – «АДВ_МНРДБЯ+_ОААИ».

Рис.6. Пример использования решетки Кардано
Магические квадраты. Магическими квадратами называются квадратные таблицы со вписанными в их клетки последовательными натуральными числами начиная с 1, которые в сумме по каждому столбцу, каждой строке и каждой диагонали дают одно и то же число. Подобные квадраты широко применялись для вписывания шифруемого текста по приведенной в них нумерации. Если потом выписать содержимое таблицы по строкам, то получалась шифровка перестановкой букв. На первый взгляд кажется, будто магических квадратов очень мало. Тем не менее, их число очень быстро возрастает с увеличением размера квадрата. Так, существует лишь один магический квадрат размером 3х3, если не принимать во внимание его повороты. Магических квадратов 4х4 насчитывается уже 880, а число магических квадратов размером 5х5 около 250000. Поэтому магические квадраты больших размеров могли быть хорошей основой для надежной системы шифрования того времени, потому что ручной перебор всех вариантов ключа для этого шифра был немыслим.
|
|
|
Рассмотри квадрат размером 4х4. В него вписываются числа от 1 до 16. Его магия состоит в том, что сумма чисел по строкам, столбцам и полным диагоналям равняется одному и тому же числу - 34. Впервые эти квадраты появились в Китае, где им и была приписана некоторая «магическая сила».

Рис.8. Магический квадрат 4х4
Шифрование по магическому квадрату производилось следующим образом. Например, требуется зашифровать фразу: «АБРАМОВДЯДИНА...». Буквы этой фразы вписываются последовательно в квадрат согласно записанным в них числам: позиция буквы в предложении соответствует порядковому числу. В пустые клетки ставится точка или любая буква.

Рис.9. Пример шифрования с помощью магического квадрата
После этого шифрованный текст записывается в строку (считывание производится слева-направо сверху-вниз, построчно) – «.РБАМДИДЯОВНА..А».
|
|
|


