 |
Системы линейных уравнений
|
|
|
|
Общий вид системы
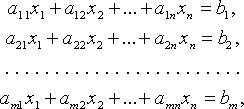
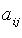, i = 1, 2,..., m; j = 1, 2,..., n, - коэффициенты системы; 
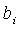- свободные члены; 
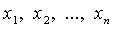- переменные;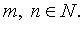 
Если все 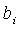= 0, система называется однородной.
Матричная запись системы линейных уравнений
AX = B,
где 
Матрицу A называют матрицей (или основной матрицей) системы. Матрицу 
называют расширенной матрицей системы, а матрицу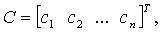 
для которой AС = В, - вектор-решением системы.
Вопрос 19.
Теорема. (Правило Крамера):
Теорема. Система из n уравнений с n неизвестными
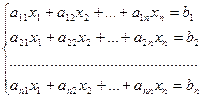
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
xi = Di/D, где
D = det A, а Di – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.
Di =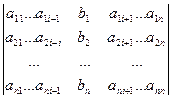 
Вопрос 20.
(см. лекцию)
Вопрос 21.
Системой m линейных уравнений с n неизвестными называется система вида
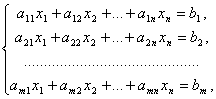
где aij и bi (i=1,…,m; b=1,…,n) – некоторые известные числа, а x1,…,xn – неизвестные. В обозначении коэффициентов aij первый индекс iобозначает номер уравнения, а второй j– номер неизвестного, при котором стоит этот коэффициент.
Коэффициенты при неизвестных будем записывать в виде матрицы 
, которую назовём матрицей системы.
Числа, стоящие в правых частях уравнений, b1,…,bm называются свободными членами.
Совокупность n чисел c1,…,cn называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c1,…,cn вместо соответствующих неизвестных x1,…,xn.
Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:
Система может иметь единственное решение.
Система может иметь бесконечное множество решений. Например, 
. Решением этой системы является любая пара чисел, отличающихся знаком.
|
|
|
И третий случай, когда система вообще не имеет решения. Например, 
, если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.
Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называетсянесовместной.
Рассмотрим способы нахождения решений системы.
МЕТОД ГАУССА
Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.
Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:
.
Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x1. Для этого второе уравнение разделим на а21 и умножим на –а11, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а31 и умножим на –а11, а затем сложим с первым. В результате исходная система примет вид: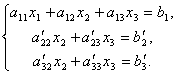 
Теперь из последнего уравнения исключим слагаемое, содержащее x2. Для этого третье уравнение разделим на 
, умножим на 
и сложим со вторым. Тогда будем иметь систему уравнений:
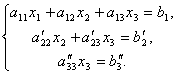
Отсюда из последнего уравнения легко найти x3, затем из 2-го уравнения x2 и, наконец, из 1-го – x1.
При использовании метода Гаусса уравнения при необходимости можно менять местами.
Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:
и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.
К элементарным преобразованиям матрицы относятся следующие преобразования:
перестановка строк или столбцов;
|
|
|
умножение строки на число, отличное от нуля;
прибавление к одной строке другие строки.
Вопрос 22.
Любая однородная система линейных алгебраических уравнений, ранг матрицы которой равен r, с помощью элементарных преобразований может быть приведена к каноническому виду:
Общее решение однородной линейной системы, записанной в каноническом виде, очевидно, определяется формулами:
Свободные переменные x r +1, x r +2,..., x m −1, x m могут принимать произвольные значения.
Вычисленные по этим формулам n − r линейно независимых решений образуют фундаментальную систему решений:
Тогда общее решение системы можно записать в вектороной форме в виде:
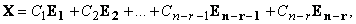
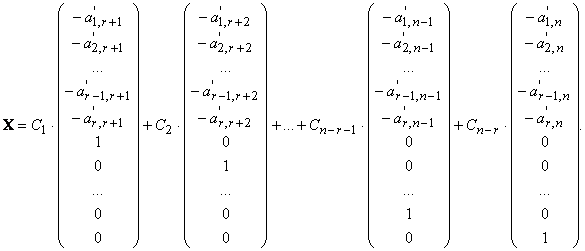
Здесь С 1, С 2,..., Сn − r −1, Сn − r — произвольные константы.
Вопрос 23.
Квадратичные формы.
Определение: Однородный многочлен второй степени относительно переменных х1 и х2
Ф(х1, х2) = а 11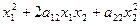 
не содержащий свободного члена и неизвестных в первой степени называется квадратичной формой переменных х1 и х2.
Определение: Однородный многочлен второй степени относительно переменных х1, х2 и х3
не содержащий свободного члена и неизвестных в первой степени называется квадратичной формой переменных х1, х2 и х3.
Рассмотрим квадратичную форму двух переменных. Квадратичная форма имеет симметрическую матрицу А =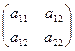 
. Определитель этой матрицы называется определителем квадратичной формы.
Пусть на плоскости задан ортогональный базис 
. Каждая точка плоскости имеет в этом базисе координаты х1, х2.
Если задана квадратичная форма Ф(х1, х2) = а 11 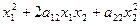, то ее можно рассматривать как функцию от переменных х1 и х2.
|
|
|
