 |
Системы линейных уравнений
|
|
|
|
Рассмотрим матричное уравнение вида
 (4.5)
(4.5)
где 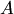 и
и  — данные матрицы, имеющие одинаковое количество строк, причем матрица
— данные матрицы, имеющие одинаковое количество строк, причем матрица 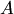 квадратная. Требуется найти матрицу
квадратная. Требуется найти матрицу  , удовлетворяющую уравнению (4.5).
, удовлетворяющую уравнению (4.5).
Теорема 4.2 о существовании и единственности решения матричного уравнения (4.5). Если определитель матрицы 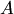 отличен от нуля, то матричное уравнение (4.5) имеет единственное решение
отличен от нуля, то матричное уравнение (4.5) имеет единственное решение  .
.
В самом деле, подставляя  в левую часть равенства (4.5), получаем
в левую часть равенства (4.5), получаем  , т.е. правую часть этого равенства.
, т.е. правую часть этого равенства.
Заметим, что решением матричного уравнения  служит обратная матрица
служит обратная матрица  .
.
Рассмотрим также матричное уравнение вида
 (4.6)
(4.6)
г де 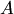 и
и  — данные матрицы, имеющие одинаковое количество столбцов, причем матрица
— данные матрицы, имеющие одинаковое количество столбцов, причем матрица 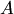 квадратная. Требуется найти матрицу
квадратная. Требуется найти матрицу  , удовлетворяющую уравнению (4.6).
, удовлетворяющую уравнению (4.6).
Теорема 4.3 о существовании и единственности решения матричного уравнения (4.6). Если определитель матрицы 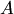 отличен от нуля, то уравнение (4.6) имеет единственное решение
отличен от нуля, то уравнение (4.6) имеет единственное решение  .
.
Заметим, что матрица  является как бы "левым" частным от "деления" матрицы
является как бы "левым" частным от "деления" матрицы  на матрицу
на матрицу 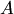 , поскольку матрица
, поскольку матрица  в (4.5) умножается на
в (4.5) умножается на 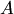 слева, а матрица
слева, а матрица  — "правым" частным, так как матрица
— "правым" частным, так как матрица  в (4.6) умножается на
в (4.6) умножается на 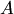 справа.
справа.
Вопрос 6.
Теорема. (Правило Крамера):
Теорема. Система из n уравнений с n неизвестными

в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
xi = Di/D, где
D = det A, а Di – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.
Di = 
Вопрос 8.
Системы линейных уравнений
Общий вид системы

 , i = 1, 2,..., m; j = 1, 2,..., n, - коэффициенты системы;
, i = 1, 2,..., m; j = 1, 2,..., n, - коэффициенты системы;  - свободные члены;
- свободные члены;  - переменные;
- переменные; 
|
|
|
Если все  = 0, система называется однородной.
= 0, система называется однородной.
Матричная запись системы линейных уравнений
AX = B,
где 
Матрицу A называют матрицей (или основной матрицей) системы. Матрицу 
называют расширенной матрицей системы, а матрицу  для которой AС = В, - вектор-решением системы.
для которой AС = В, - вектор-решением системы.
Вопрос 9.
Системой m линейных уравнений с n неизвестными называется система вида

где aij и bi (i=1,…,m; b=1,…,n) – некоторые известные числа, а x1,…,xn – неизвестные. В обозначении коэффициентов aij первый индекс iобозначает номер уравнения, а второй j– номер неизвестного, при котором стоит этот коэффициент.
Коэффициенты при неизвестных будем записывать в виде матрицы  , которую назовём матрицей системы.
, которую назовём матрицей системы.
Числа, стоящие в правых частях уравнений, b1,…,bm называются свободными членами.
Совокупность n чисел c1,…,cn называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c1,…,cn вместо соответствующих неизвестных x1,…,xn.
Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:
Система может иметь единственное решение.
Система может иметь бесконечное множество решений. Например,  . Решением этой системы является любая пара чисел, отличающихся знаком.
. Решением этой системы является любая пара чисел, отличающихся знаком.
И третий случай, когда система вообще не имеет решения. Например,  , если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.
, если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.
Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называетсянесовместной.
Рассмотрим способы нахождения решений системы.
МЕТОД ГАУССА
Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.
|
|
|
Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:
 .
.
Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x1. Для этого второе уравнение разделим на а21 и умножим на –а11, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а31 и умножим на –а11, а затем сложим с первым. В результате исходная система примет вид: 
Теперь из последнего уравнения исключим слагаемое, содержащее x2. Для этого третье уравнение разделим на  , умножим на
, умножим на  и сложим со вторым. Тогда будем иметь систему уравнений:
и сложим со вторым. Тогда будем иметь систему уравнений:

Отсюда из последнего уравнения легко найти x3, затем из 2-го уравнения x2 и, наконец, из 1-го – x1.
При использовании метода Гаусса уравнения при необходимости можно менять местами.
Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:

и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.
К элементарным преобразованиям матрицы относятся следующие преобразования:
перестановка строк или столбцов;
умножение строки на число, отличное от нуля;
прибавление к одной строке другие строки.
Вопрос 10
Линейное (векторное) пространство.
Как известно, линейные операции (сложение, вычитание, умножение на число) определены по-своему для каждого множества (числа, многочлены, направленные отрезки, матрицы). Сами операции различны, но их свойства одинаковы.
Эта общность свойств позволяет обобщить понятие линейных операций для любых множеств вне зависимости от того, что это за множества (числа, матрицы и т.д.).
Для того, чтобы дать определение линейного (векторного) пространства рассмотрим некоторое множество L действительных элементов, для которых определены операции сложения и умножения на число.
Эти операции обладают свойствами:
1) Коммутативность  +
+  =
=  +
+ 
2) Ассоциативность ( +
+  ) +
) +  =
=  + (
+ ( +
+  )
)
3)Существует такой нулевой вектор  , что
, что  +
+  =
=  для "
для "  Î L
Î L
4) Для "  Î L существует вектор
Î L существует вектор  = -
= -  , такой, что
, такой, что  +
+  =
= 
5)1×  =
= 
6) a(b  ) = (ab)
) = (ab) 
7) Распределительный закон (a + b)  = a
= a  + b
+ b 
8) a( +
+  ) = a
) = a  + a
+ a 
|
|
|
Определение: Множество L называется линейным (векторным) пространством, а его элементы называются векторами.
Свойства линейных пространств.
1) В каждом линейном пространстве существует только один нулевой элемент.
2) Для каждого элемента существует только один противоположный элемент.
3) Для каждого  Î L верно 0×
Î L верно 0×  = 0
= 0
4) Для каждого a Î R и  Î L верно a×
Î L верно a×  =
= 
5) Если a×  =
=  , то a = 0 или
, то a = 0 или  =
= 
6) (-1)  = -
= - 
Линейные преобразования.
Определение: Будем считать, что в линейном пространстве L задано некоторое линейное преобразование А, если любому элементу  Î L по некоторому правилу ставится в соответствие элемент А
Î L по некоторому правилу ставится в соответствие элемент А  Î L.
Î L.
Определение: Преобразование А называется линейным, если для любых векторов  Î L и
Î L и  Î L и любого a верно:
Î L и любого a верно:
A( +
+  ) = A
) = A  +A
+A 
A(a  ) = aA
) = aA 
Определение: Линейное преобразование называется тождественным, если оно преобразует элемент линейного пространства сам в себя.
Е  =
= 
Определение: Если  только при a = b = … = l = 0, то векторы
только при a = b = … = l = 0, то векторы  называются линейно независимыми.
называются линейно независимыми.
Определение. Линейными операциями над векторами называется сложение и умножение на число.
Суммой векторов является вектор - 
Произведение - 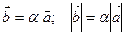 , при этом
, при этом  коллинеарен
коллинеарен  .
.
Вектор  сонаправлен с вектором
сонаправлен с вектором  (
(
 ), если a > 0.
), если a > 0.
Вектор  противоположно направлен с вектором
противоположно направлен с вектором  (
( ¯
¯  ), если a < 0.
), если a < 0.
Вопрос 11
Определение.
1) Базисом в пространстве называются любые 3 некомпланарных вектора, взятые в определенном порядке.
2) Базисом на плоскости называются любые 2 неколлинеарные векторы, взятые в определенном порядке.
3) Базисом на прямой называется любой ненулевой вектор.
Линейная зависимость векторов.
Определение. Векторы  называются линейно зависимыми, если существует такая линейная комбинация
называются линейно зависимыми, если существует такая линейная комбинация  , при не равных нулю одновременно ai, т.е.
, при не равных нулю одновременно ai, т.е.  .
.
Если же только при ai = 0 выполняется  , то векторы называются линейно независимыми.
, то векторы называются линейно независимыми.
Свойство 1. Если среди векторов  есть нулевой вектор, то эти векторы линейно зависимы.
есть нулевой вектор, то эти векторы линейно зависимы.
Свойство 2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.
|
|
|
Свойство 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.
Свойство 4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны.
Свойство 5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны.
Свойство 6. Любые 4 вектора линейно зависимы.
Определение. Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице.
Вопрос 12.
Скалярное произведение векторов.
Определение. Скалярным произведением векторов  и
и  называется число, равное произведению длин этих сторон на косинус угла между ними.
называется число, равное произведению длин этих сторон на косинус угла между ними.

 ×
×  = ï
= ï  ïï
ïï  ïcosj
ïcosj
Свойства скалярного произведения:
1)  ×
×  = ï
= ï  ï2;
ï2;
2)  ×
×  = 0, если
= 0, если  ^
^  или
или  = 0 или
= 0 или  = 0.
= 0.
3)  ×
×  =
=  ×
×  ;
;
4)  ×(
×( +
+  ) =
) =  ×
×  +
+  ×
×  ;
;
5) (m  )×
)×  =
=  ×(m
×(m  ) = m(
) = m( ×
×  );
);
Если рассматривать векторы  в декартовой прямоугольной системе координат, то
в декартовой прямоугольной системе координат, то

 ×
×  = xa xb + ya yb + za zb;
= xa xb + ya yb + za zb;
Используя полученные равенства, получаем формулу для вычисления угла между векторами:

 ;
;
Вопрос 13
Векторное произведение векторов.
Определение. Векторным произведением векторов  и
и  называется вектор
называется вектор  , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям:
1)  , где j - угол между векторами
, где j - угол между векторами  и
и  ,
,

2) вектор  ортогонален векторам
ортогонален векторам  и
и 
3)  ,
,  и
и  образуют правую тройку векторов.
образуют правую тройку векторов.
 Обозначается:
Обозначается:  или
или  .
.


j

Свойства векторного произведения векторов:
1) 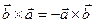 ;
;
2) 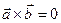 , если
, если  ïï
ïï  или
или  = 0 или
= 0 или  = 0;
= 0;
3) (m  )´
)´  =
=  ´(m
´(m  ) = m(
) = m( ´
´  );
);
4)  ´(
´( +
+  ) =
) =  ´
´  +
+  ´
´  ;
;
 5) Если заданы векторы
5) Если заданы векторы  (xa, ya, za) и
(xa, ya, za) и  (xb, yb, zb) в декартовой прямоугольной системе координат с единичными векторами
(xb, yb, zb) в декартовой прямоугольной системе координат с единичными векторами 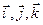 , то
, то
 ´
´  =
= 
6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах  и
и  .
.
Вопрос 14
Смешанное произведение векторов.
Определение. Смешанным произведением векторов  ,
,  и
и  называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора  на вектор, равный векторному произведению векторов
на вектор, равный векторному произведению векторов  и
и  .
.
Обозначается  или (
или ( ,
,  ,
,  ).
).
Смешанное произведение  по модулю равно объему параллелепипеда, построенного на векторах
по модулю равно объему параллелепипеда, построенного на векторах  ,
,  и
и  .
.





Свойствасмешанного произведения:
1)Смешанное произведение равно нулю, если:
а)хоть один из векторов равен нулю;
б)два из векторов коллинеарны;
в)векторы компланарны.
2) 
3) 
4) 
5) Объем треугольной пирамиды, образованной векторами  ,
,  и
и  , равен
, равен
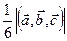
6)Если  ,
,  , то
, то 
|
|
|


