Основные законы геометрической оптики

Оптика

Оптика – раздел физики, изучающий свойства и физическую природу света, а также его взаимодействие с веществом. Учение о свете принято делить на три части:

• геометрическая или лучевая оптика, в основе которой лежит представление о световых лучах;
• волновая оптика, изучающая явления, в которых проявляются волновые свойства света;
• квантовая оптика, изучающая взаимодействие света с веществом, при котором проявляются корпускулярные свойства света.

В настоящей главе рассматриваются две первые части оптики. Корпускулярные свойства света будут рассматриваться в гл. V.

Геометрическая оптика

Основные законы геометрической оптики

Основные законы геометрической оптики были известны задолго до установления физической природы света.

Закон прямолинейного распространения света: в оптически однородной среде свет распространяется прямолинейно. Опытным доказательством этого закона могут служить резкие тени, отбрасываемые непрозрачными телами при освещении светом источника достаточно малых размеров («точечный источник»). Другим доказательством может служить известный опыт по прохождению света далекого источника сквозь небольшое отверстие, в результате чего образуется узкий световой пучок. Этот опыт приводит к представлению о световом луче как о геометрической линии, вдоль которой распространяется свет. Следует отметить, что закон прямолинейного распространения света нарушается и понятие светового луча утрачивает смысл, если свет проходит через малые отверстия, размеры которых сравнимы с длиной волны. Таким образом, геометрическая оптика, опирающаяся на представление о световых лучах, есть предельный случай волновой оптики при λ → 0. Границы применимости геометрической оптики будут рассмотрены в разделе о дифракции света.

На границе раздела двух прозрачных сред свет может частично отразиться так, что часть световой энергии будет распространяться после отражения по новому направлению, а часть пройдет через границу и продолжит распространяться во второй среде.

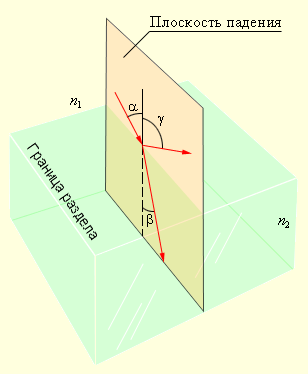
Закон отражения света: падающий и отраженный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости (плоскость падения). Угол отражения γ равен углу падения α.

Закон преломления света: падающий и преломленный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости. Отношение синуса угла падения α к синусу угла преломления β есть величина, постоянная для двух данных сред:

Закон преломления был экспериментально установлен голландским ученым В. Снеллиусом в 1621 г.

Постоянную величину n называют относительным показателем преломления второй среды относительно первой. Показатель преломления среды относительно вакуума называют абсолютным показателем преломления.

Относительный показатель преломления двух сред равен отношению их абсолютных показателей преломления:

n = n 2 / n 1.

Законы отражения и преломления находят объяснение в волновой физике. Согласно волновым представлениям, преломление является следствием изменения скорости распространения волн при переходе из одной среды в другую. Физический смысл показателя преломления – это отношение скорости распространения волн в первой среде υ₁ к скорости их распространения во второй среде υ₂:

Абсолютный показатель преломления равен отношению скорости света c в вакууме к скорости света υ в среде:

Рис 3.1.1 иллюстрирует законы отражения и преломления света.

Рисунок 3.1.1. Законы отражения и преломления: γ = α; n 1 sin α = n 2 sin β.

Среду с меньшим абсолютным показателем преломления называют оптически менее плотной.

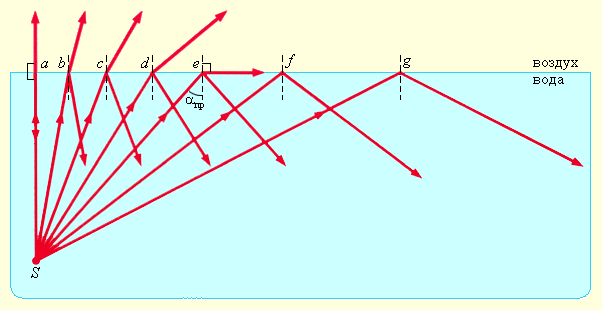
При переходе света из оптически более плотной среды в оптически менее плотную n ₂ < n ₁ (например, из стекла в воздух) можно наблюдать явление полного отражения, то есть исчезновение преломленного луча. Это явление наблюдается при углах падения, превышающих некоторый критический угол α_пр, который называется предельным углом полного внутреннего отражения (см. рис. 3.1.2).

Для угла падения α = α_пр sin β = 1; значение sin α_пр = n ₂ / n ₁ < 1.

Если второй средой является воздух (n ₂ ≈ 1), то формулу удобно переписать в виде

sin αпр = 1 / n,

где n = n ₁ > 1 – абсолютный показатель преломления первой среды.

Для границы раздела стекло–воздух (n = 1,5) критический угол равен α_пр = 42°, для границы вода–воздух (n = 1,33) α_пр = 48,7°.

Рисунок 3.1.2. Полное внутреннее отражение света на границе вода–воздух; S – точечный источник света

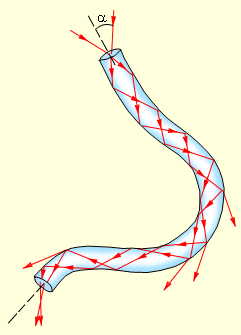
Явление полного внутреннего отражения находит применение во многих оптических устройствах. Наиболее интересным и практически важным применением является создание волоконных световодов, которые представляют собой тонкие (от нескольких микрометров до миллиметров) произвольно изогнутые нити из оптически прозрачного материала (стекло, кварц). Свет, попадающий на торец световода, может распространяться по нему на большие расстояния за счет полного внутреннего отражения от боковых поверхностей (рис 3.1.3). Научно-техническое направление, занимающееся разработкой и применением оптических световодов, называется волоконной оптикой.

Рисунок 3.1.3. Распространение света в волоконном световоде. При сильном изгибе волокна закон полного внутреннего отражения нарушается, и свет частично выходит из волокна через боковую поверхность

Модель. Отражение и преломление света

 

Зеркала

Простейшим оптическим устройством, способным создавать изображение предмета, является плоское зеркало. Изображение предмета, даваемое плоским зеркалом, формируется за счет лучей, отраженных от зеркальной поверхности. Это изображение является мнимым, так как оно образуется пересечением не самих отраженных лучей, а их продолжений в «зазеркалье» (рис 3.2.1).

Рисунок 3.2.1. Ход лучей при отражении от плоского зеркала. Точка S' является мнимым изображением точки S

Вследствие закона отражения света мнимое изображение предмета располагается симметрично относительно зеркальной поверхности. Размер изображения равен размеру самого предмета.

Сферическим зеркалом называют зеркально отражающую поверхность, имеющую форму сферического сегмента. Центр сферы, из которой вырезан сегмент, называют оптическим центром зеркала. Вершину сферического сегмента называют полюсом. Прямая, проходящая через оптический центр и полюс зеркала, называется главной оптической осью сферического зеркала. Главная оптическая ось выделена из всех других прямых, проходящих через оптический центр, только тем, что она является осью симметрии зеркала.

Сферические зеркала бывают вогнутыми и выпуклыми. Если на вогнутое сферическое зеркало падает пучок лучей, параллельный главной оптической оси, то после отражения от зеркала лучи пересекутся в точке, которая называется главным фокусом F зеркала. Расстояние от фокуса до полюса зеркала называют фокусным расстоянием и обозначают той же буквой F. У вогнутого сферического зеркала главный фокус действительный. Он расположен посередине между центром и полюсом зеркала (рис 3.2.2).

Рисунок 3.2.2. Отражение параллельного пучка лучей от вогнутого сферического зеркала. Точки O – оптический центр, P – полюс, F – главный фокус зеркала; OP – главная оптическая ось, R – радиус кривизны зеркала

Следует иметь в виду, что отраженные лучи пересекаются приблизительно в одной точке только в том случае, если падающий параллельный пучок был достаточно узким (так называемый параксиальный пучок).

Главный фокус выпуклого зеркала является мнимым. Если на выпуклое зеркало падает пучок лучей, параллельных главной оптической оси, то после отражения в фокусе пересекутся не сами лучи, а их продолжения (рис 3.2.3).

Рисунок 3.2.3. Отражение параллельного пучка лучей от выпуклого зеркала. F – мнимый фокус зеркала, O – оптический центр; OP – главная оптическая ось

Фокусным расстояниям сферических зеркал приписывается определенный знак: для вогнутого зеркала для выпуклого где R – радиус кривизны зеркала.

Изображение какой-либо точки A предмета в сферическом зеркале можно построить с помощью любой пары стандартных лучей:

• луч AOC, проходящий через оптический центр зеркала; отраженный луч COA идет по той же прямой;
• луч AFD, идущий через фокус зеркала; отраженный луч идет параллельно главной оптической оси;
• луч AP, падающий на зеркало в его полюсе; отраженный луч симметричен с падающим относительно главной оптической оси.
• луч AE, параллельный главной оптической оси; отраженный луч EFA ₁ проходит через фокус зеркала.

На рис 3.2.4 перечисленные выше стандартные лучи изображены для случая вогнутого зеркала. Все эти лучи проходят через точку A', которая является изображением точки A. Все остальные отраженные лучи также проходят через точку A'. Ход лучей, при котором все лучи, вышедшие из одной точки, собираются в другой точке, называется стигматическим. Отрезок A'B' является изображением предмета AB. Аналогичны построения для случая выпуклого зеркала.

Рисунок 3.2.4. Построение изображения в вогнутом сферическом зеркале

Положение изображения и его размер можно также определить с помощью формулы сферического зеркала:

Здесь d – расстояние от предмета до зеркала, f – расстояние от зеркала до изображения. Величины d и f подчиняются определенному правилу знаков:

• d > 0 и f > 0 – для действительных предметов и изображений;
• d < 0 и f < 0 – для мнимых предметов и изображений.

Для случая, изображенного на рис 3.2.4, имеем:

F > 0 (зеркало вогнутое); d = 3 F > 0 (действительный предмет).

По формуле сферического зеркала получаем: следовательно, изображение действительное.

Если бы на месте вогнутого зеркала стояло выпуклое зеркало с тем же по модулю фокусным расстоянием, мы получили бы следующий результат:

F < 0, d = –3 F > 0, – изображение мнимое.

Линейное увеличение сферического зеркала Γ определяется как отношение линейных размеров изображения h ' и предмета h.

Величине h ' удобно приписывать определенный знак в зависимости от того, является изображение прямым (h' > 0) или перевернутым (h' < 0). Величина h всегда считается положительной. При таком определении линейное увеличение сферического зеркала выражается формулой, которую можно легко получить из рис 3.2.4:

В первом из рассмотренных выше примеров – следовательно, изображение перевернутое, уменьшенное в 2 раза. Во втором примере – изображение прямое, уменьшенное в 4 раза.

Модель. Плоское зеркало

Модель. Сферическое зеркало

Тонкие линзы

Линзой называется прозрачное тело, ограниченное двумя сферическими поверхностями. Если толщина самой линзы мала по сравнению с радиусами кривизны сферических поверхностей, то линзу называют тонкой.

Линзы входят в состав практически всех оптических приборов. Линзы бывают собирающими и рассеивающими. Собирающая линза в середине толще, чем у краев, рассеивающая линза, наоборот, в средней части тоньше (рис. 3.3.1).

Рисунок 3.3.1. Собирающие (a) и рассеивающие (b) линзы и их условные обозначения

Прямая, проходящая через центры кривизны O ₁ и O ₂ сферических поверхностей, называется главной оптической осью линзы. В случае тонких линз приближенно можно считать, что главная оптическая ось пересекается с линзой в одной точке, которую принято называть оптическим центром линзы O. Луч света проходит через оптический центр линзы, не отклоняясь от первоначального направления. Все прямые, проходящие через оптический центр, называются побочными оптическими осями.

Если на линзу направить пучок лучей, параллельных главной оптической оси, то после прохождения через линзу лучи (или их продолжения) соберутся в одной точке F, которая называется главным фокусом линзы. У тонкой линзы имеются два главных фокуса, расположенных симметрично на главной оптической оси относительно линзы. У собирающих линз фокусы действительные, у рассеивающих – мнимые. Пучки лучей, параллельных одной из побочных оптических осей, после прохождения через линзу также фокусируются в точку F', которая расположена при пересечении побочной оси с фокальной плоскостью Ф, то есть плоскостью, перпендикулярной главной оптической оси и проходящей через главный фокус (рис. 3.3.2). Расстояние между оптическим центром линзы O и главным фокусом F называется фокусным расстоянием. Оно обозначаетcя той же буквой F.

Рисунок 3.3.2. Преломление параллельного пучка лучей в собирающей (a) и рассеивающей (b) линзах. Точки O 1и O 2 – центры сферических поверхностей, O 1 O 2 – главная оптическая ось, O – оптический центр, F – главный фокус, F' – побочный фокус, OF' – побочная оптическая ось, Ф – фокальная плоскость

Основное свойство линз – способность давать изображения предметов. Изображения бывают прямыми и перевернутыми, действительными и мнимыми, увеличенными и уменьшенными.

Положение изображения и его характер можно определить с помощью геометрических построений. Для этого используют свойства некоторых стандартных лучей, ход которых известен. Это лучи, проходящие через оптический центр или один из фокусов линзы, а также лучи, параллельные главной или одной из побочных оптических осей. Примеры таких построений представлены на рис. 3.3.3 и 3.3.4.

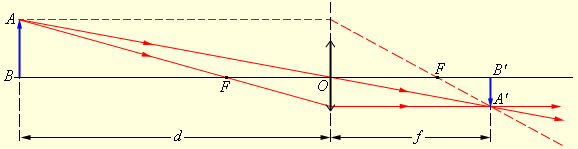
Рисунок 3.3.3. Построение изображения в собирающей линзе

 

Рисунок 3.3.4. Построение изображения в рассеивающей линзе

Следует обратить внимание на то, что некоторые из стандартных лучей, использованных на рис. 3.3.3 и 3.3.4 для построения изображений, не проходят через линзу. Эти лучи реально не участвуют в образовании изображения, но они могут быть использованы для построений.

Положение изображения и его характер (действительное или мнимое) можно также рассчитать с помощью формулы тонкой линзы. Если расстояние от предмета до линзы обозначить через d, а расстояние от линзы до изображения через f, то формулу тонкой линзы можно записать в виде:

Величину D, обратную фокусному расстоянию. называют оптической силой линзы. Единицой измерения оптической силы является диоптрия (дптр). Диоптрия – оптическая сила линзы с фокусным расстоянием 1 м:

1 дптр = м–1.

Формула тонкой линзы аналогична формуле сферического зеркала. Ее можно получить для параксиальных лучей из подобия треугольников на рис. 3.3.3 или 3.3.4.

Фокусным расстояниям линз принято приписывать определенные знаки: для собирающей линзы F > 0, для рассеивающей F < 0.

Величины d и f также подчиняются определенному правилу знаков:
d > 0 и f > 0 – для действительных предметов (то есть реальных источников света, а не продолжений лучей, сходящихся за линзой) и изображений;
d < 0 и f < 0 – для мнимых источников и изображений.

Для случая, изображенного на рис. 3.3.3, имеем: F > 0 (линза собирающая), d = 3 F > 0 (действительный предмет).

По формуле тонкой линзы получим: следовательно, изображение действительное.

В случае, изображенном на рис. 3.3.4, F < 0 (линза рассеивающая), d = 2| F | > 0 (действительный предмет), то есть изображение мнимое.

В зависимости от положения предмета по отношению к линзе изменяются линейные размеры изображения. Линейным увеличением линзы Γ называют отношение линейных размеров изображения h' и предмета h. Величине h', как и в случае сферического зеркала, удобно приписывать знаки плюс или минус в зависимости от того, является изображение прямым или перевернутым. Величина h всегда считается положительной. Поэтому для прямых изображений Γ > 0, для перевернутых Γ < 0. Из подобия треугольников на рис. 3.3.3 и 3.3.4 легко получить формулу для линейного увеличения тонкой линзы:

В рассмотренном примере с собирающей линзой (рис. 3.3.3): d = 3 F > 0, следовательно, – изображение перевернутое и уменьшенное в 2 раза.

В примере с рассеивающей линзой (рис. 3.3.4): d = 2| F | > 0, ; следовательно, – изображение прямое и уменьшенное в 3 раза.

Оптическая сила D линзы зависит как от радиусов кривизны R ₁ и R ₂ ее сферических поверхностей, так и от показателя преломления n материала, из которого изготовлена линза. В курсах оптики доказывается следующая формула:

Радиус кривизны выпуклой поверхности считается положительным, вогнутой – отрицательным. Эта формула используется при изготовлении линз с заданной оптической силой.

Во многих оптических приборах свет последовательно проходит через две или несколько линз. Изображение предмета, даваемое первой линзой, служит предметом (действительным или мнимым) для второй линзы, которая строит второе изображение предмета. Это второе изображение также может быть действительным или мнимым. Расчет оптической системы из двух тонких линз сводится к двукратному применению формулы линзы, при этом расстояние d ₂ от первого изображения до второй линзы следует положить равным величине l – f ₁, где l – расстояние между линзами. Рассчитанная по формуле линзы величина f ₂ определяет положение второго изображения и его характер (f ₂ > 0 – действительное изображение, f ₂ < 0 – мнимое). Общее линейное увеличение Γ системы из двух линз равно произведению линейных увеличений обеих линз: Γ = Γ₁ · Γ₂. Если предмет или его изображение находятся в бесконечности, то линейное увеличение утрачивает смысл.

Частным случаем является телескопический ход лучей в системе из двух линз, когда и предмет, и второе изображение находятся на бесконечно больших расстояниях. Телескопический ход лучей реализуется в зрительных трубах – астрономической трубе Кеплера и земной трубе Галилея (см. § 3.5).

Тонкие линзы обладают рядом недостатков, не позволяющих получать высококачественные изображения. Искажения, возникающие при формировании изображения, называются аберрациями. Главные из них – сферическая и хроматическая аберрации. Сферическая аберрация проявляется в том, что в случае широких световых пучков лучи, далекие от оптической оси, пересекают ее не в фокусе. Формула тонкой линзы справедлива только для лучей, близких к оптической оси. Изображение удаленного точечного источника, создаваемое широким пучком лучей, преломленных линзой, оказывается размытым.

Хроматическая аберрация возникает вследствие того, что показатель преломления материала линзы зависит от длины волны света λ. Это свойство прозрачных сред называется дисперсией. Фокусное расстояние линзы оказывается различным для света с разными длинами волн, что приводит к размытию изображения при использовании немонохроматического света.

В современных оптических приборах применяются не тонкие линзы, а сложные многолинзовые системы, в которых удается приближенно устранить различные аберрации.

Формирование собирающей линзой действительного изображения предмета используется во многих оптических приборах, таких как фотоаппарат, проектор и т. д.

Фотоаппарат представляет собой замкнутую светонепроницаемую камеру. Изображение фотографируемых предметов создается на фотопленке системой линз, которая называется объективом. Специальный затвор позволяет открывать объектив на время экспозиции.

Особенностью работы фотоаппарата является то, что на плоской фотопленке должны получаться достаточно резкими изображения предметов, находящихся на разных расстояниях.

В плоскости фотопленки получаются резкими только изображения предметов, находящихся на определенном расстоянии. Наведение на резкость достигается перемещением объектива относительно пленки. Изображения точек, не лежащих в плоскости резкого наведения, получаются размытыми в виде кружков рассеяния. Размер d этих кружков может быть уменьшен путем диафрагмирования объектива, т.е. уменьшения относительного отверстия a / F (рис. 3.3.5). Это приводит к увеличению глубины резкости.

Рисунок 3.3.5. Фотоаппарат

Проекционный аппарат предназначен для получения крупномасштабных изображений. Объектив O проектора фокусирует изображение плоского предмета (диапозитив D) на удаленном экране Э (рис. 3.3.6). Система линз K, называемая конденсором, предназначена для того, чтобы сконцентрировать свет источника S на диапозитиве. На экране Э создается действительное увеличенное перевернутое изображение. Увеличение проекционного аппарата можно менять, приближая или удаляя экран Э с одновременным изменением расстояния между диапозитивом D и объективом O.

Рисунок 3.3.6. Проекционный аппарат

Модель. Тонкая линза

Модель. Система из двух линз

 

1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: