 |
Анализ плоского напряженного состояния и оценка прочности материала в опасной точке детали.
|
|
|
|
Сборник заданий
Построение эпюры крутящих моментов Mк
Пример 1. Определить момент М пр на приводном колесе вала по заданным силовым факторам. Построить эпюры крутящих моментов Mк для вала, изображенного на рис.20 а). Здесь в точках А,В и D приложены сосредоточенные крутящие моменты на колесах, а на участке ВС – распределенный крутящий момент, например, на шнеке. Опоры (подшипники) условно не показаны.
Заданные величины: М 1=200 Н·м; М 2=180 Н·м; q =120 Н·м/м; l 1=0,2 м; l 2=0,5 м; l 3=0,15 м.
1. Изобразим расчетную схему (рис.20 б). Определим приводной момент, для чего составим уравнение равновесия (моментов) относительно оси вала х.
2. Для построения эпюр разобьем характерными точками вал на участки. Здесь три участка нагружения. Определим на каждом участке закон изменения Mк. Последовательность участков следует сделать такой, чтобы эти законы были по возможности проще – так, чтобы в каждом из них было минимум учитываемых силовых факторов. Например, это можно сделать, как это показано на схеме.
1-й участок (АВ):
Нм – величина постоянная на всем участке.
2-й участок (DC):
Нм –постоянный на всем участке.
3-й участок (CB):
прямая. Следует определить значения M к в двух точках – обычно их определяют на концах участка.
Нм;
Нм.
По полученным данным построим эпюру M к (Рис. 20 в). В данном случае правильность эпюры подтверждается тем, что скачек ее в точке В составил 200 Нм, что соответствует приложенному сосредоточенному моменту М 1
Задача 1. Определить момент М пр на приводном колесе вала по заданным силовым факторам. Построить эпюры крутящих моментов M к для вала, изображенного на расчетной схеме, выбранной в соответствии с присвоенным студенту кодом. Данные для расчета выбираются из таблицы 1 также в соответствии кодом.
|
|
|
Таблица 1
| цифра | 1-я | 2-я | 3-я | 4-я | 5-я | 1-я | 2-я |
| схема | l 1, м | l 2, м | l 3, м | M 1, Нм | M 2, Нм | q, Нм/м | |
| 0,2 | 0,6 | 0,4 | |||||
| 0,3 | 0,5 | 0,5 | |||||
| 0,4 | 0,4 | 0,6 | |||||
| 0,5 | 0,3 | 0,2 | |||||
| 0,6 | 0,2 | 0,3 | |||||
| 0,2 | 0,6 | 0,4 | |||||
| 0,3 | 0,5 | 0,5 | |||||
| 0,4 | 0,4 | 0,6 | |||||
| 0,5 | 0,3 | 0,2 | |||||
| 0,6 | 0,2 | 0,3 |
Построение эпюр продольных N и поперечных Qy сил, и изгибающих моментов Mz
Пример 1. Построить эпюры внутренних силовых факторов (ВСФ) для консольной балки (Рис.20).
1. Поскольку балка консольная, реакции в защемлении можно не определять, но все зависимости при определении ВСФ придется в этом случае «тащить» со свободного ее конца.
Характерные сечения − A,B,C,D,E. Участки нагружения − AB,BC,CD,DE.
Из схемы видно, что нормальное усилие действует только на участке BE. N(II−IV)=−P1cosα=− 3,46 кН по всей длине II − IV участков, что показано на эпюре N (Рис.20 б).
2. Эпюры Qy и Mz сложнее, поэтому рассмотрим их по участкам:
1 − й участок.
Q(I)y=−P2+qx1=− 4+2 x1; − прямая.
M(I)z=P2x1−q(x21)/ 2 = 4 x1− 2 (x21)/ 2; − квадратичная парабола.
В характерных точках:
кН; 
кН.
Эпюра Q(I)y при x1= 2м меняет знак, следовательно эпюра M в этом сечении имеет экстремум. Поэтому М(I)z определяем в трех точках.
, 
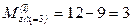, кНм, 
кНм.
2 − й участок.
;
+
;
кН; 
кН;
кНм; 
кНм,
кНм.
3 − й участок.
кН − по всему участку.
; 
кНм;
кНм;
4 − й участок.
кН − по всему участку.
;
кНм; 
кНм.
3. По полученным результатам построены эпюры N, Qy и Mz (Рис.20 б,в,г).
Пример 2. Построить эпюры внутренних силовых факторов для простой двухопорной балки (Рис.21).
1. Реакции опор определятся:
, откуда
кН.
,
кН.
Проверка:
Реакции YA и YB определены верно.
Реакция XA определится из уравнения: ΣX=−XA+q 1(cosα) · 4=0, откуда XA=q 1(cos 60º) · 4 =2,0 кН.
|
|
|
2. В данном случае, поскольку реакции опор определены, чтобы не "тащить" все внешние силовые факторы вдоль всей балки, рациональнее строить эпюры с двух ее концов, для чего разобьем балку на участки нагружения AB, BC, CD и DC, как это показано на рисунке 21.
3. Определим зависимости внутренних силовых факторов по участкам.
1 − й участок.
N(I)=−XA = − 2,0 кН − по всему участку. Q(I)y=YA−q1 x1; 
кН; 
кН. 
− парабола. 
в сечении x1=YA/q1 =2,4/2=1,2 м. Определяем 
в трех точках: 
; 
кН · м; 
кН · м;
2 − й участок.
N(II)=−XA = − 2,0 кН − по всему участку. Q(II)y=YA−q1· 2=2,4 − 2 · 2= = − 1,6 кН − по всему участку; M(II)z=YA (2 +x2−q1 2(2/2+ x2) +M − прямая. Достаточно определить M(II)z в 2 − х сечениях. 
=2,4(2+0) − 2× ×2(2/2+0)+4=4,8 кН · м; 
=2,4(2+1) − 2 2(2/2+1)+4=3,2 кН · м;
3 − й участок.
N(III)=−q2 cos α·x3 − прямая. 
=0; 
= − 1 · cos60 º· 2= − 1кН; Q(III)y=q2sinα·x3 − прямая; 
=0; 
=1 · sin60 º 2=1,73 кН. M(III)z=−q2sinα·x32 /2 − парабола. Имеет экстремум в сечении x3= 0, т.е. на конце балки. Определяем в трех точках: 
=0; 
= − 1·sin60 º ×1 2 /2= − 0,43 кН · м; 
= − 1·(sin60 º) · 2 2 /2= − 1,73 кН · м;
4 − й участок.
N(IV)=−q2 ·cos α· (2+ x4) − прямая. 
= − 1 · cos60 º (2+0)= − 1 кН; 
= − 1 · cos60 º· (2+2)= = − 2 кН; Q(IV)y=q2· sin α ·(2+ x4) −YD − прямая; 
=1 · sin60 º· (2+0) − 5,06= − 3,33 кН; 
=1 · sin60 º ·(2+2) − 5,06= − 1,6кН; 
= −q2· sin α· (2+x 4) 2 /2+ YD·x4 − парабола. 
= − 1·sin60 º ×(2+0) 2 /2+5,06 · 0= − 1,73 кН · м;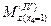 
= − 1·sin60 º· (2+1) 2 /2+5,06 · 1=1,16 кН · м; 
= − 1·sin60 º· (2+2) 2 /2+5,06 · 2=3,20 кН · м;
4. По полученным результатам построены эпюры N, Qy и Mz (Рис.21 б,в,г).
Задача 2. Построить эпюры внутренних силовых факторов (ВСФ) для консольной балки, изображенной на расчетной схеме, выбранной в соответствии с присвоенным студенту кодом. Данные для расчета выбираются из таблицы 2 также в соответствии кодом.
Таблица 2
| цифра | 1-я | 2-я | 3-я | 4-я | 5-я | 1-я | 2-я | 3-я | 4-я |
| схема | l 1, м | l 2, м | l 3, м | l 4, м | Р 1, кН | Р 2, кН | M, кНм | q, кН/м | |
| 1,0 | 1,5 | 2,5 | 2,2 | ||||||
| 1,2 | 1,6 | 1,8 | 2,4 | ||||||
| 1,4 | 1,8 | 2,0 | 2,5 | ||||||
| 1,5 | 2,0 | 3,0 | 2,6 | ||||||
| 1,6 | 2,2 | 1,5 | 2,8 | ||||||
| 1,8 | 2,4 | 2,5 | 3,0 | ||||||
| 2,0 | 2,5 | 2,6 | 1,5 | ||||||
| 2,2 | 2,6 | 2,8 | 1,8 | ||||||
| 2,4 | 2,8 | 2,2 | 2,0 | ||||||
| 2,5 | 3,0 | 2,4 | 2,5 |
|
|
|
Анализ плоского напряженного состояния и оценка прочности материала в опасной точке детали.
Пример 1. В опасной точке детали, выполненной из пластичного материала с пределом текучести σт=250 МПа, коэффициентом Пуассона μ=0,3, произвести анализ плоского напряженного состояния, заданного напряжениями на двух взаимно перпендикулярных площадках, и оценить прочность материла в данной точке (рис.4.12), если нормативный коэффициент запаса прочности [ n ]=1,5. Исходные данные: σ x =80 МПа, σ у =–40 МПа, τ= –50 МПа, Е=2·105 МПа. Знаки взяты по расчетной схеме (Рис.?) согласно принятым правилам. Определить напряжения на площадках, соответствующих углу α= –60°,
Решение.
1. Определяем положения главных площадок:
2. Находим величины главных напряжений:
Таким образом, σ1=σmax=98 МПа, σ2=0 (т.к. напряженное состояние плоское), σ3=σmin= –58 МПа.
Положение главных площадок и действующие на них главные напряжения показаны на рис.??. Для этого отложим от нормали к вертикальной площадке против часовой (т.к. знак “–”) стрелки угол α0=–αгл=19,90°, получим направление большего по величине главного напряжения σ1=98 МПа, (так как σ x >σ у,то угол α0 определяет положение главной площадки, где действует σmax). На перпендикулярной ей главной площадке действует напряжение σ3= –58 МПа.
3. Определим напряжения на взаимно перпендикулярных площадках, повернутых относительно исходных на угол α=–60°.
4. Наибольшие касательные напряжения:
5. Эквивалентное напряжение по четвертой теории прочности:
6. Определение коэффициента запаса прочности.
Прочность детали обеспечена.
7. Главные деформации:
8. Определим относительное изменение объема.
Задача 3.
Произвести анализ плоского напряженного состояния и оценить прочность материала в опасной точке детали по заданным напряжениям на двух взаимно-перпендикулярных наклонных площадках. Если материал детали пластичный, то предел текучести принять σт=280 МПа, если хрупкий, то предел прочности при растяжении σвр=200 МПа, при сжатии σвс=550 МПа
|
|
|
Коэффициентом Пуассона μ=0,29, нормативный коэффициент запаса прочности принять [ n ]=1,4, модуль Юнга Е=2·105 МПа.
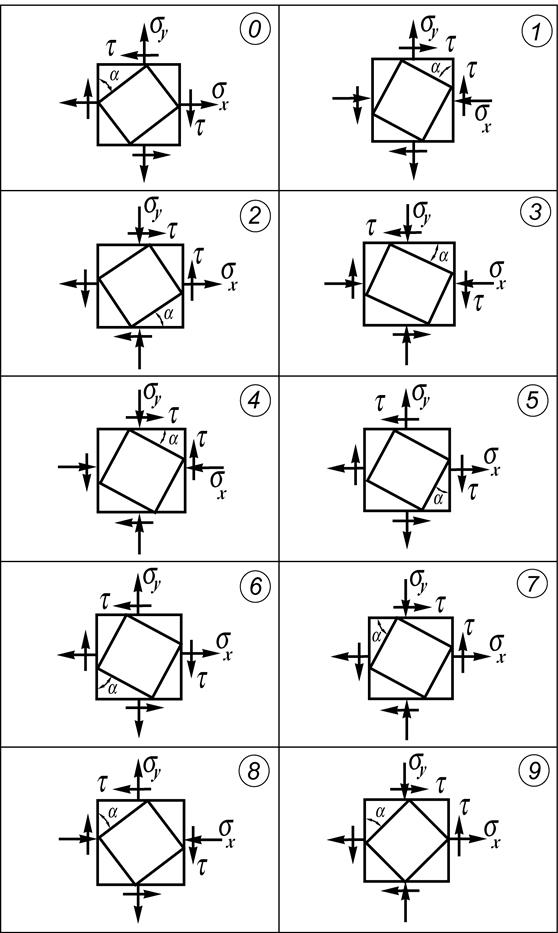
Прочие числовые данные и расчетная схема выбираются в соответствие с шифром из таблицы 3. и рис. 3
Таблица 3
| цифра | 1-я | 2-я | 3-я | 4-я | 1-я | 2-я |
| схема | |σ x |, МПа | |σ у |, МПа | |τ|, МПа | α° | Материал: | |
| пластичн. | ||||||
| хрупкий | ||||||
| пластичн. | ||||||
| хрупкий | ||||||
| пластичн. | ||||||
| хрупкий | ||||||
| пластичн. | ||||||
| хрупкий | ||||||
| пластичн. | ||||||
| хрупкий |
Содержание и порядок выполнения задания.
1. Вычертить схему элемента с соответствующими напряжениями.
2. Определить знаки напряжений и углов в соответствии со схемой.
3. Определить положение главных площадок и значения главных напряжений.
4. Определить напряжения на взаимно перпендикулярных площадках, повернутых на угол α относительно исходных площадок.
5. Вычислить наибольшие касательные напряжения.
6. Вычислить эквивалентные напряжения и определить коэффициенты запаса прочности: а) для пластичного материала по теориям прочности наибольших касательных напряжений и потенциальной энергии изменения формы; б) для хрупкого материала но теории наибольших линейных.деформаций и теории прочности Мора.
7. Определить главные деформации.
8. Вычислить относительное изменение объема.
|
|
|
