 |
Синтез цифровых рекурсивных фильтров с использованием
|
|
|
|
Пакета MATLAB
Решение задачи синтеза цифровых рекурсивных фильтров(РФ) сводится к нахождению коэффициентов ak и bk разностного уравнения:

| (9.1) |
Известны прямые и косвенные методы синтеза рекурсивных цифровых фильтров[4,1]. Прямые методы основаны на непосредственном определении параметров цифровых РФ по заданным временным или частотным характеристикам. Косвенные методы синтеза цифровых РФ основаны на дискретизации аналогового фильтра-прототипа, удовлетворяющего заданным требованиям. Существуют различные способы аппроксимации аналоговых фильтров[6,1]. На практике широко применяется аппроксимация АЧХ аналоговых фильтров с помощью полиномов Баттерворта, Чебышева, Бесселя, Кауэра.
При проектировании фильтров обычно задают следующие требования к их амплитудно-частотным характеристикам(АЧХ):
- границы полос пропускания и задерживания (соответственно w1 и w2);
- затухание в полосе задерживания (Н2);
- коэффициент передачи в полосе пропускания(Н1- обычно он равен 1);
- допуск на отклонение реальной АЧХ от желаемой в полосе пропускания(D1).
В пакете МATLAB для синтеза РФ существует ряд функций:
- butter – аппроксимация фильтра Баттерворта;
- cheby 1 – аппроксимация фильтра Чебышева первого типа;
- cheby 2 – аппроксимация фильтра Чебышева второго типа(инверсный фильтр Чебышева);
- ellip – аппроксимация эллиптического фильтра(фильтр Кауэра).
Например, вызов функции butter в пакете MATLAB может иметь следующий синтаксис:
[b,a] = butter(n,Wn);
[b,a] = butter(n,Wn,'ftype').
Для расчета порядка фильтра Баттерворта, обеспечивающего требуемые характеристики(Н1, Н2, D1) в пакете MATLAB используется функция buttord, имеющая следующий синтаксис:
[n,Wn] = buttord(Wp,Ws,Rp,Rs).
|
|
|
Пример. С помощью пакета MATLAB найти коэффициенты и построить характеристики полосового фильтра Баттерворта с полосой пропускания от 60 до 200Гц(частота дискретизации 1кГц), с пульсациями в полосе пропускания не более 3 дБ и затуханием в полосе задерживания не менее 40 дБ.
Ниже представлен текст программы, а на рисунке 9.4 показаны характеристики полученного фильтра.
Wp = [60 200]/500; %расчет нормированных граничных частот полосы пропускания
Ws = [50 250]/500; %расчет нормированных граничных частот полосы задерживания
Rp = 3; Rs = 40;% задаем величину пульсаций и затухание
[n,Wn] = buttord(Wp,Ws,Rp,Rs)% определяем порядок фильтра и частоты среза
>> n =16
>> Wn =[0.1198 0.4005]
[ b, a ] = butter (n, Wn);%находим коэффициенты фильтра
freqz(b,a,128,1000)% строим характеристики фильтра
title ('АЧХ и ФЧХ полосового фильтра Баттерворта')
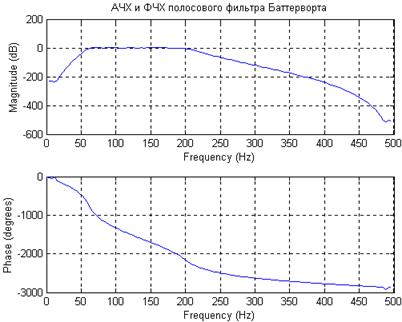 |
Рисунок 9.4 - АЧХ и ФЧХ полосового фильтра Баттерворта
Синтез гребенки фильтров
От числа частотных полос зависит разборчивость синтезированной речи. Хорошие результаты получаются при числе каналов 15-16 (полоса 100 Гц... 4 кГц). По условию поставленной задачи необходимо разработать вокодер для сжатия и передачи по каналу связи речи без идентификации диктора, то для уменьшения количества передаваемой информации можно уменьшить количество каналов до 12-14. На рисунке 3.1 представлена реализация используемой при кодировании гребенки фильтров, состоящей из 12 полосовых фильтров, ФНЧ и ФВЧ.

Рисунок 3.1 – гребанка фильтров.
Нижеследующий текст программы на матлабе позволяет рассчитать необходимые характеристики фильтров и построить АЧХ гребенки фильтров.
n_bands = 15;
fd1 = 8000
[n,Wn] = buttord(100/fd1, 300/fd1, 2, 50);
[b{1},a{1}] = butter(n, Wn);
[n,Wn] = buttord([125/fd1 300/fd1], [20/fd1 500/fd1], 4, 40);
[b{2},a{2}] = butter(n, Wn);
[n,Wn] = buttord([305/fd1 485/fd1], [105/fd1 685/fd1], 3, 40);
[b{3},a{3}] = butter(n, Wn);
[n,Wn] = buttord([500/fd1 690/fd1], [300/fd1 890/fd1], 3, 40);
[b{4},a{4}] = butter(n, Wn);
[n,Wn] = buttord([700/fd1 880/fd1], [500/fd1 1080/fd1], 2, 40);
|
|
|
[b{5},a{5}] = butter(n, Wn);
[n,Wn] = buttord([900/fd1 1080/fd1], [700/fd1 1280/fd1], 2, 40);
[b{6},a{6}] = butter(n, Wn);
[n,Wn] = buttord([1100/fd1 1380/fd1], [900/fd1 1580/fd1], 2, 45);
[b{7},a{7}] = butter(n, Wn);
[n,Wn] = buttord([1400/fd1 1680/fd1], [1200/fd1 1880/fd1], 2, 47);
[b{8},a{8}] = butter(n, Wn);
[n,Wn] = buttord([1700/fd1 1980/fd1], [1500/fd1 2180/fd1], 2, 50);
[b{9},a{9}] = butter(n, Wn);
[n,Wn] = buttord([2000/fd1 2330/fd1], [1800/fd1 2530/fd1], 2, 50);
[b{10},a{10}] = butter(n, Wn);
[n,Wn] = buttord([2350/fd1 2670/fd1], [2150/fd1 2870/fd1], 2, 50);
[b{11},a{11}] = butter(n, Wn);
[n,Wn] = buttord([2700/fd1 3070/fd1], [2500/fd1 3270/fd1], 2, 50);
[b{12},a{12}] = butter(n, Wn);
[n,Wn] = buttord([3100/fd1 3470/fd1], [2900/fd1 3670/fd1], 2, 50);
[b{13},a{13}] = butter(n, Wn);
[n,Wn] = buttord([3500/fd1 3880/fd1], [3300/fd1 4080/fd1], 2, 50);
[b{14},a{14}] = butter(n, Wn);
[n,Wn] = buttord(3900/fd1, 3700/fd1, 2, 50);
[b{n_bands},a{n_bands}] = butter(n, Wn, 'high');
hold on;
for i=1:n_bands,
[H,W] = freqz(b{i}, a{i}, [0:0.01:pi]);
plot(W,20*log10(abs(H)));
axis([0 pi -100 10]);
end;
hold off;
Гребенка состоит из цифровых фильтров Баттерворта, так как это наиболее распространенный БИХ-фильтров.
|
|
|


