 |
Полная волновая функция атома.
|
|
|
|
Метод Слейтера – решаем для каждого электрона
(1/2 ∇2е1 + (E + Zэфф/r1)y = 0 для 1-го электрона,
1/2 ∇2 е2 + (E + Zэфф/r2)y = 0 для 2-го электрона
или в общем случае S (1/2 ∇2 еi + (E + Zэфф/ri)y) = 0
Окончательно имеем:
Решение для многоэлектронного атома имеет вид
y(r, j,J,)= Rn,l(r)* ql,m (J)* Fm (j) = f(n,l,m) E = Zэфф2/2nэфф 2= f(nэфф) =f(n, l)
• Величины nэфф и n связаны между собою.
N 1 2 3 4 5 6
nэфф 1 2 3 3,7 4,0 4,2
Хорошо видно, что n =1,2,3 = nэфф
Учитывая, что E =f(n, l) зависимость АО по энергии выглядит так

Выводы:
1.Pезультат одноэлектроного приближения – это зависимость E = f(n,l) вместо E =f(n) для атома H. Снимается вырождение E по l.
Главное квантовое число n потеряло физический смысл для многоэлектронной модели.
Угловые часть волновой функции полностью совпадает с Y(J,j) для атома водорода.
Радиальная часть волновой функции индивидуальна для каждого атома и не может быть представлена в простом виде.
Рассмотрим решение для нескольких АО
Нормированные волновые функции водородоподобных атомов
(Равдель Краткий справочник физико – химических величин., 1999, стр 163)
где r = Zr/a0
Y1s0 = 1/Öp *(Z/a0)3/2 e-r = A * R(r);
Y2s0 = 1/4Ö2p *(Z/a0)3/2(2-r) e-r =B* R(r)
Y2p0 = 1/4Ö2p *(Z/a0)3/2(2-r) e-r* cos J =B* R(r) * cos J
Y2p1 = 1/4Ö2p *(Z/a0)3/2(2-r) e-rsinJcosj =B* R(r) * sinJcosj
Y2p-1 = 1/4Ö2p *(Z/a0)3/2(2-r) e-r sinJsinj =B * R(r)* sinJsinj
Y3s0= 2/81Ö3p *(Z/a0)3/2(27-18r + 2r2) e-r/3 =C * R(r)
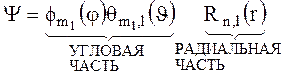
Хорошо видно, что для любой АО ns- типа угловая часть имеет одинаковый вид: Yns0 = A * R(r), т.е при любых значениях углов (J и j) получаем константу, т.е. форма сфера.
Для анализа радикальной части определяем количество узловых точек на зависимости R(r)=f(r) по уравнению n- l -1 и наносим их на спадающую экспоненту. В коллоквиуме студент вправе выбрать любую АО валентного слоя и проанализировать ее форму
|
|
|
Распределение атомных орбиталей по энергии.
Основной принцип распределения АО по энергии – это принцип минимума энергии.
Распределение по энергии АО соответствует полученному решению для энергии E = f(n,l), т.е. по мере увеличения n и l энергия АО увеличивается в ряду 1s < 2s < 2p < 3s < 3p, т.к. n = n (от 1-3)
Начиная с n = 4 наблюдается нарушение в заполнении уровней, т.к.
n ¹ nэфф и E(4s) становится меньше чем E(3d).
Все эти особенности учитываются ПРАВИЛАМИ КЛЕЧКОВСКОГО.
1. Энергия уровня растет с ростом (n + l)
2. При одинаковых значениях (n + l) минимуму энергии соответствует АО с минимальным значением n.
Задача. Запишите все АО заданного многоэлектронного атома и распределите их по энергии. (показать на любом примере)
Полная волновая функция атома.
Напомним, что если на АО находится 1 электрон то состояние этого электрона описывается волновой функцией электрона или спин-орбиталью
cе =Y(n,l,ml)*s(ms) = f(n,l,ml,ms).
Состояние системы содержащей несколько электронов описывается полной волновой функцией, учитывающей квантовые состояния для всех электронов, т.е. совокупностью спин-орбиталей.
cат = П cеi (П – произведение)
Такая функция может быть записана в кратком эмпирическом виде.
Одна из форм записи полной функции хорошо известна - это электронная конфигурация.
ЭЛЕКТРОННОЙ КОНФИГУРАЦИЕЙ-- называется распределение электронов атома по различным квантовым состояниям (или спин-орбиталям).
Общий вид: Пnili Ni, где k - количество электронов на данной АО или подуровне (т.е. общее кол-во на всех АО с одинаковым значением l).
Например для атома H - 1s1, He - 1s2, C - 1s2 2s2 2p2.
Несмотря на широкое применение электронной конфигурации такая форма записи имеет существенный недостаток, т.к. не дает информацию о реальном распределении электронов по квантовым ячейкам.
Другой формой записи полной волновой функцией является
|
|
|
АТОМНЫЙ ТЕРМ.
Теперь можно дать общее выражение для атомного терма, описывающего общее состояние многоэлектронного атома для схемы
Рассел -Саундерса (Энергетическая характеристика)
T = 2S+1Lj
Символ терма определяется по величине квантового числа L
-----------------------------------------------
- Символ терма S P D F H Аналогично обозначению
L 0 1 2 3 4 атомных орбиталей
-------------------------------------------------
Величина M = 2S + 1 называется мультиплетностью и показывает число линий на которое расщепляется основной сигнал.
Терм основного состояния (с мин. энергии) можно определить по максимальным значениям результирующих квантовых чисел.
L =[å mli ], S = [å msi ]
|
|
|


