Задачи линейного программирования

1. В задачах линейного программирования значение целевой функции может стремиться к (укажите верные ответы):

· Min,

· Max,

· Const,

· 0.

 

2. Дана следующая задача линейного программирования:

Предприятие может выпускать изделия трех видов, которые продаются по ценам соответственно 30 у.е., 40 у.е. и 60 у.е. за штуку. Трудовые ресурсы предприятия ограничены величиной 180 чел.-час. На производство одного изделия первого вида затрачивается 5 чел.- часов, второго вида – 6 чел.-часов, а производство одного изделия третьего вида требует 12 чел – часов. Найти оптимальную производственную программу выпуска изделий трех видов, которая обеспечивает предприятию максимальную выручку.

Выберите правильный вариант записи целевой функции:

f) 30х₁+40х₂+60х₃ 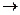max

g) 30х₁+40х₂+60х₃ 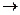min

h) 5х₁+6х₂+12х₃ 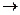min

i) 5х₁+6х₂+12х₃ 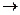max

j) х₁+х₂+х₃ 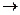max

k) х₁+х₂+х₃ 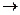min

 

3. Верно ли утверждение, что оптимальное решение является допустимым?

· да,

· нет.

4. Верно ли утверждение, что допустимое решение является оптимальным?

· да,

· нет.

5. Целевая функция задачи линейного программирования выражает:

· критерий оптимальности,

· количество израсходованных ресурсов,

· значения переменных,

 

6. Ограничения задачи линейного программирования делятся на:

· функциональные и прямые,

· прямые и двойственные,

· функциональные и линейные.

 

7. Оптимальное решение задачи линейного программирования это:

· набор данных Х, при котором целевая функция достигает наибольшего или наименьшего значения,

· допустимое значение плана Х, при котором целевая функция достигает наибольшего или наименьшего значения,

· набор данных Х, который удовлетворяет системе ограничений,

· неотрицательное значение плана Х.

8. Задача линейного программирования может быть решена (укажите верные ответы):

· симплекс-методом,

· графическим методом,

· методом Крамера

· методом наименьших квадратов.

 

9. Выберите верное продолжение утверждения:

Все задачи оптимизации используются для:

· выбора наилучшего решения из множества возможных,

· оптимального планирования количества используемых ресурсов,

· определения наилучшего капиталовложения.

 

10. Задача математического программирования, для которой процесс решения имеет пошаговый характер, называется:

· линейной

· нелинейной

· статической

· динамической

· целочисленной.

 

11. Выберите верное продолжение утверждения:

В любой задаче линейного программирования совокупность ограничений определяет …

· Область допустимых решений

· Пределы использование ресурсов,

· Возможные значения переменных,

· Возможные значения целевой функции

 

12. Дана следующая задача линейного программирования:

Предприятие может выпускать изделия трех видов, которые продаются по ценам соответственно 30 у.е., 40 у.е. и 60 у.е. за штуку. Трудовые ресурсы предприятия ограничены величиной 180 чел.-час. На производство одного изделия первого вида затрачивается 5 чел.- часов, второго вида – 6 чел.-часов, а производство одного изделия третьего вида требует 12 чел – часов. Найти оптимальную производственную программу выпуска изделий трех видов, которая обеспечивает предприятию максимальную выручку.

Выберите правильный вариант системы ограничений:

 

a)

b)

c)

d)

e)

13. На кондитерской фабрике весь ассортимент выпускаемой карамели разделен на три однородные группы, условно обозначенные K₁, K₂, K₃. Расход основного сырья и его запас указаны в таблице. Другие виды сырья, входящие в готовый продукт в небольших количествах, не учитываются. Составить план производства карамели, при котором достигается максимум прибыли.

Виды основного сырья	Расход сырья на 1 т	Общий запас сырья
K1	K2	K3
I (сахарный песок)	0,7	0,7	0,7
II (патока)	0,3	0,3	0,2
III (фруктовое пюре)		0,2	0,3
Уровень прибыли

 

Укажите правильный вариант выбора переменных:

a) x₁, x₂, x₃ - количество карамели каждой группы

b) x₁, x₂, x₃ - количество используемого сахарного песка, патоки и фруктового пюре

c) x₁, x₂, x₃ - прибыль от производства карамели каждой группы

Поделиться:

Воспользуйтесь поиском по сайту: