 |
Взлом полиалфавитных шифров
|
|
|
|
Шифр Виженера
Шифр Виженера (фр. Chiffre de Vigenère) - метод полиалфавитного шифрования буквенного текста с использованием ключевого слова.
Этот метод является простой формой многоалфавитной замены. Шифр Виженера изобретался многократно. Впервые этот метод описал Джован Баттиста Беллазо (итал. Giovan Battista Bellaso) в книге La cifra del. Sig. Giovan Battista Bellaso в 1553 году, однако, в XIX веке получил имя Блеза Виженера, французского дипломата. Метод прост для понимания и реализации, он является недоступным для простых методов криптоанализа.
Описание
В шифре Цезаря каждая буква алфавита сдвигается на несколько позиций; например в шифре Цезаря при сдвиге +3, A стало бы D, B стало бы E и так далее. Шифр Виженера состоит из последовательности нескольких шифров Цезаря с различными значениями сдвига. Для зашифровывания может использоваться таблица алфавитов, называемая tabula recta или квадрат (таблица) Виженера. Применительно к латинскому алфавиту таблица Виженера составляется из строк по 26 символов, причём каждая следующая строка сдвигается на несколько позиций. Таким образом, в таблице получается 26 различных шифров Цезаря. На каждом этапе шифрования используются различные алфавиты, выбираемые в зависимости от символа ключевого слова. Например, предположим, что исходный текст имеет вид: ATTACKATDAWN
Человек, посылающий сообщение, записывает ключевое слово («LEMON») циклически до тех пор, пока его длина не будет соответствовать длине исходного текста:
LEMONLEMONLE
Первый символ исходного текста A зашифрован последовательностью L, которая является первым символом ключа. Первый символ L шифрованного текста находится на пересечении строки L и столбца A в таблице Виженера. Точно так же для второго символа исходного текста используется второй символ ключа; то есть второй символ шифрованного текста X получается на пересечении строки E и столбца T. Остальная часть исходного текста шифруется подобным способом.
|
|
|
Исходный текст: ATTACKATDAWN
Ключ: LEMONLEMONLE
Зашифрованный текст: LXFOPVEFRNHR
Расшифровывание производится следующим образом: находим в таблице Виженера строку, соответствующую первому символу ключевого слова; в данной строке находим первый символ зашифрованного текста. Столбец, в котором находится данный символ, соответствует первому символу исходного текста. Следующие символы зашифрованного текста расшифровываются подобным образом.
Если буквы A—Z соответствуют числам 0—25, то шифрование Виженера можно записать в виде формулы:
Расшифровка:
Криптоанализ
Шифр Виженера «размывает» характеристики частот появления символов в тексте, но некоторые особенности появления символов в тексте остаются. Главный недостаток шифра Виженера состоит в том, что его ключ повторяется. Поэтому простой криптоанализ шифра может быть построен в два этапа:
· Поиск длины ключа. Можно анализировать распределение частот в зашифрованном тексте с различным прореживанием. То есть брать текст, включающий каждую 2-ю букву зашифрованного текста, потом каждую 3-ю и т. д. Как только распределение частот букв будет сильно отличаться от равномерного (например, по энтропии), то можно говорить о найденной длине ключа.
· Криптоанализ. Совокупность l-шифров Цезаря (где l - найденная длина ключа), которые по отдельности легко взламываются.
Тесты Фридмана и Касиски могут помочь определить длину ключа.
Метод Касиски
В 1863 году Фридрих Касиски был первым, кто опубликовал успешный алгоритм атаки на шифр Виженера, хотя Чарльз Беббидж разработал этот алгоритм уже в 1854 году. В то время когда Беббидж занимался взломом шифра Виженера, Джон Холл Брок Твейтс представил новый шифр в «Journal of the Society of the Arts»; когда Беббидж показал, что шифр Твейтса является лишь частным случаем шифра Виженера, Твейтс предложил ему его взломать. Беббидж расшифровал текст, который оказался поэмой «The Vision of Sin» Альфреда Теннисона, зашифрованной ключевым словом Emily — именем жены поэта.
|
|
|
Тест Касиски опирается на то, что некоторые слова, такие как «the» могут быть зашифрованы одинаковыми символами, что приводит к повторению групп символов в зашифрованном тексте. Например: сообщение, зашифрованное ключом ABCDEF, не всегда одинаково зашифрует слово «crypto»:
Ключ: ABCDEF AB CDEFA BCD EFABCDEFABCD
Исходный текст: CRYPTO IS SHORT FOR CRYPTO GRAPHY
Шифрованный текст: CSASXT IT UKSWT GQU GWYQVR KWAQJB
Зашифрованный текст в данном случае не будет повторять последовательности символов, которые соответствуют повторным последовательностям исходного текста. В данном шифрованном тексте есть несколько повторяющихся сегментов, которые позволяют криптоаналитику найти длину ключа:
Ключ: ABCDAB CD ABCDA BCD ABCDABCDABCD
Исходный текст: CRYPTO IS SHORT FOR CRYPTO GRAPHY
Шифрованный текст: CSASTP KV SIQUT GQU CSASTP IUAQJB
Более длинные сообщения делают тест более точным, так как они включают в себя больше повторяющихся сегментов зашифрованного текста.
Тест Фридмана
Тест Фридмана (иногда называемый каппа-тестом) был изобретен Вильямом Фридманом в 1920 году. Фридман использовал индекс совпадения, который измеряет частоты повторения символов, чтобы взломать шифр. Зная вероятность 
того, что два случайно выбранных символа текста совпадают (примерно 0,067 для англ. языка) и вероятность совпадения двух случайно выбранных символов алфавита 
(примерно 1 / 26 = 0,0385 для англ. языка), можно оценить длину ключа как:
Из наблюдения за частотой совпадения следует:
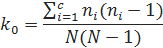
где С — размер алфавита (26 символов для англ. языка), N — длина текста, и 
— наблюдаемые частоты повторения символов зашифрованного текста. Однако, это только приблизительное значение, точность которого увеличивается при большем размере текста. На практике это было бы необходимо для перебора различных ключей приближаясь к исходному.
Частотный анализ
Как только длина ключа становится известной, зашифрованный текст можно записать во множество столбцов, каждый из которых соответствует одному символу ключа. Каждый столбец состоит из исходного текста, который зашифрован шифром Цезаря; ключ к шифру Цезаря является всего-навсего одним символом ключа для шифра Виженера, который используется в этом столбце. Используя методы, подобные методам взлома шифра Цезаря, можно расшифровать зашифрованный текст. Усовершенствование теста Касиски, известное как метод Кирхгофа, заключается в сравнении частоты появления символов в столбцах с частотой появления символов в исходном тексте для нахождения ключевого символа для этого столбца. Когда все символы ключа известны, криптоаналитик может легко расшифровать шифрованный текст, получив исходный текст. Метод Кирхгофа не применим, когда таблица Виженера скремблирована, вместо использования обычной алфавитной последовательности, хотя тест Касиски и тесты совпадения всё ещё могут использоваться для определения длины ключа для этого случая.
|
|
|
Варианты
Вариант running key (бегущий ключ) шифра Виженера когда-то был невзламываемым. Эта версия использует в качестве ключа блок текста, равный по длине исходному тексту. Так как ключ равен по длине сообщению, то методы предложенные Фридманом и Касиски не работают (так как ключ не повторяется). В 1920 году Фридман первым обнаружил недостатки этого варианта. Проблема с running key шифра Виженера состоит в том, что криптоаналитик имеет статистическую информацию о ключе (учитывая, что блок текста написан на известном языке) и эта информация будет отражаться в шифрованном тексте. Если ключ действительно случайный, его длина равна длине сообщения и он использовался единожды, то шифр Виженера теоретически будет невзламываемым, фактически этот вариант будет уже шифром Вернама-Виженера, на которую доказана абсолютная криптостойкость.
Виженер фактически изобрёл более стойкий шифр — шифр с автоключом. Несмотря на это, «шифр Виженера» ассоциируется с более простым многоалфавитным шифром. Фактически эти два шифра часто путали, называя их le chiffre indechiffrable. Беббидж фактически взломал более стойкий шифр с автоключом, в то время когда Касиски издал первое решение взлома многоалфавитного шифра с фиксированным ключом. Метод Виженера зашифровки и расшифровки сообщений иногда относится к «варианту Битфорда». Его отличие от шифра Битфорда, изобретенного сэром Френсисом Битфордом, который, тем не менее, подобен шифру Виженера, заключается в использовании немного измененного механизма шифрования и таблиц.
|
|
|
Несмотря на очевидную стойкость шифра Виженера, он широко не использовался в Европе. Большее распространение получил шифр Гронсфилда, созданный графом Гронсфилдом, идентичный шифру Виженера, за исключением того, что он использовал только 10 различных алфавитов (соответствующих цифрам от 0 до 9). Преимущество шифра Гронсфилда состоит в том, что в качестве ключа используется не слово, а недостаток — в небольшом количестве алфавитов. Шифр Гронсфилда широко использовался по всей Германии и Европе, несмотря на его недостатки.
Взлом полиалфавитных шифров
Проще всего взломать полиалфавитный шифр, зная его период, то есть число используемых моноалфавитных шифров. Тогда, выбрав буквы, соответствующие каждому из моноалфавитных шифров, можно к каждому из них применить так называемый частотный анализ (или какой-нибудь другой метод взлома моноалфавитных шифров). Метод основан на том, что каждая буква в произвольном тексте появляется с вполне определенной частотой, а значит, посмотрев частоты появления тех или иных букв, можно узнать, как происходит замена. Одним из методов нахождения периода полиалфавитных шифров является метод, предложенный Фредериком Касиски в 1836 году. Он заключается в том, что в зашифрованном тексте находятся одинаковые сегменты длины не меньше, чем три буквы, затем вычисляются расстояния между первыми буквами соседних сегментов. Оказывается, предполагаемый период является кратным наибольшему общему делителю для этих расстояний.
Список литературы:
А. В. Яковлев, А. А. Безбогов, В. В. Родин, В. Н. Шамкин «Криптографическая защита информации».
Э. М. Габидулин «Курс лекций по Защите Информации»
А. П. Алферов, А. Ю. Зубов, А. С. Кузьмин, А. В. Черёмушкин «Основы криптографии»
|
|
|
