Описание установки и метода измерений

Кафедра физики

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ № 2 м.ф.

“Определение средней длины свободного пробега и эффективного диаметра молекул воздуха”.

 

Составили: Самсонова Н.П.,

Ярков Д.М

Тюмень, 2004 г.

№ 2. м.ф. ОПРЕДЕЛЕНИЕ СРЕДНЕЙ ДЛИНЫ СВОБОДНОГО ПРОБЕГА И ЭФФЕКТИВНОГО ДИАМЕТРА МОЛЕКУЛ ВОЗДУХА.

 

ЦЕЛЬ РАБОТЫ: измерение средней длины свободного пробега и эффективного диаметра молекул воздуха.

ОБОРУДОВАНИЕ: сосуд с водой, капилляр, секундомер.

 

КРАТКАЯ ТЕОРИЯ

Согласно молекулярно - кинетической теории, хаотическое молекулярное движение является причиной наблюдаемых в газах явлений переноса: перенос энергии при выравнивании температур (теплопроводность), перенос массы при выравнивании концентраций (диффузия), перенос импульса при выравнивании скоростей (вязкость).

Хотя величины скоростей молекул относительно велики и могут достигать сотен метров в секунду, процессы переноса совершаются сравнительно медленно. Происходит это потому, что молекулы непрерывно соударяются друг с другом. Между двумя последовательными соударениями молекулы движутся прямолинейно и равномерно, проходя в среднем расстояние, называемое средней длиной свободного пробега молекулы.

Столкновения молекул характеризуются эффективным диаметром. Эффективным диаметром d молекулы называется минимальное расстояние между центрами двух молекул, на которое они могут сблизиться при столкновении.

Молекулярно - кинетическая теория позволяет при помощи легко измеряемых макроскопических параметров (давления, объёма, температуры) получить интересующие нас микроскопические параметры - эффективные размеры молекул и её среднюю длину свободного пробега.

Для определения средней длины свободного пробега l молекул газа используют формулу связи коэффициента внутреннего трения (вязкости) h с и (средней арифметической скоростью молекул):

(1)

r - плотность газа.

Из уравнения Менделеева - Клапейрона:

(2)

Средняя скорость молекул

(3)

Подставляя в формулу (1) значения r и из уравнения (2) и (3), получим:

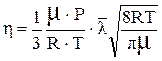(4)

В данной работе для измерения пользуются методом истечения газа через капиллярную трубку малого диаметра.

Объём V газа, протекающего через трубку с круглым внутренним сечением радиуса r за время t, определяется по формуле Паузейля:

, (5)

DР - разность давлений на концах капилляра, которой и обусловлено течение газа, l - длина капилляра.

Из уравнения (5) коэффициент вязкости:

(6)

Сравнивая уравнения (4) и (6), получим следующую формулу для определения средней длины свободного пробега:

(7)

Эффективный диаметр d молекул вычисляют из формулы, выражающей его связь со средней длиной свободного пробега `l:

, (8)

n - число молекул газа в единице объёма при данных условиях (концентрация молекул). Из основного уравнения кинетической теории газов для величины нормального давления Р₀ и давления в лаборатории, получаем равенство:

Р₀ = n₀kT₀, (9)

Р = nkT, (10)

n₀ = 2,69×10²⁵ м^-3 - число Лошмидта, т.е. число молекул газа в единице объёма при нормальных условиях (Т₀ = 273К, Р₀ = 101,33кПа); k --постоянная Больцмана.

Из уравнения (9) и (10) находим:

. (11)

Решая уравнение (8) относительно d и учитывая уравнение (11), получим:

(12)

 

 

ОПИСАНИЕ УСТАНОВКИ И МЕТОДА ИЗМЕРЕНИЙ

Схема опытной установки приведена на рисунке 1.

Сосуд А, заполненный водой и снабжённый шкалой, имеет кран В для выпускания жидкости. Сквозь пробку в сосуд пропущен капилляр С, радиус и длина которого известны. Капилляр не должен касаться поверхности воды.

При закрытом кране В давление воздуха над жидкостью внутри сосуда равно атмосферному, т.к. сосуд сообщается с атмосферой через капилляр. Если приоткрыть кран В, то вследствие вытекания воды давление в сосуде будет уменьшаться и в него через капилляр будет засасываться воздух. Обладая определённой вязкостью, воздух постепенно просачивается сквозь капилляр, в результате чего внутри сосуда давление газа остается ниже атмосферного. Такой процесс засасывания через капилляр воздуха и истечение из сосуда жидкости будет происходить до тех пор, пока суммарное давление газа и жидкости на уровне отверстия не станет равным атмосферному, т.е.:

Р_атм = Р^/ + rgh,

Р^/ - давление воздуха в сосуде при открытом кране В, r - плотность воды, h - высота столба воды в данный момент.

Истечение жидкости происходит под действием её гидростатического давления, определяемого высотой столба жидкости над уровнем отверстия. При этом на концах капилляра установится разность давлений:

DР = Р_атм - Р^/ = rgh,

вызывающая протекание воздуха через капилляр в сосуд. Эта разность со временем уменьшается из-за снижения высоты столба жидкости. Т.к. площадь сечения сосуда велика, а объём вытекающей жидкости мы выбираем сравнительно малым, то изменение высоты столба жидкости и давления DР будет незначительным. Поэтому в формуле (7) в качестве DР можно взять среднюю разность давлений на концах капилляра в начале и в конце опыта, т.е.:

, (13)

h₁ - первоначальный уровень воды (в момент открытия крана),

h₂ - установившийся уровень после вытекания некоторого объёма воды (в момент закрытия крана).

Объём V протекшего через капилляр газа будет равен объёму жидкости, вытекшей через кран В в мерный стакан Д.

 

ХОД РАБОТЫ

1. Сосуд А должен быть наполнен на ³/₄ водой. Отметить уровень воды h₁.

2. Открыть кран В и, дождавшись, когда вода начнёт вытекать из сосуда каплями, включить секундомер.

3. Когда в стакане соберётся 40-60см³ воды, закрыть кран В, одновременно останавливая секундомер.

4. Отметить новый уровень воды h₂. Записать показания секундомера t.

5. Измерить по соответствующим приборам давление Р и температуру Т воздуха в лаборатории.

6. Данные записать в таблицу (измерения произвести не менее 3^х раз).

h1, м	h2, м	t, с	V, м3	Т, К	Р, Па	r, м	l, м

 

7. По формуле (13) вычислить значение DР.

8. По формуле (7) и (12) определить соответственно среднюю длину свободного пробега и эффективный диаметр молекул воздуха ( и d).

9. Рассчитать погрешности измерений величин `l и d и записать окончательные результаты измерений:

`l = `l_ср ± D`l; d = d_ср ± Dd.

 

ПРИЛОЖЕНИЕ

* Для капилляра r = (0,15 ± 0,01) мм,

l = (46,0 ± 0,1) мм.

* Молярная масса воздуха m = 0,029 кг/моль.

* Плотность воды r = 10³ кг/м³.

* Нормальные условия Р₀ = 101,33×10³ Па,

Т₀ = 273 К,

n₀ = 2,69×10²⁵ м^-3.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ.

1. Что называется средней длиной свободного пробега, эффективным диаметром молекул, средним числом столкновений в единицу времени? Запишите связь между этими величинами.

2. Запишите уравнение Менделеева - Клапейрона и выразите его через плотность r газа. Получите из уравнения Менделеева - Клапейрона уравнение, связывающее давление Р и концентрацию n молекул.

3. В чём заключаются явления переноса? Запишите уравнения теплопроводности, внутреннего трения, диффузии (закон Фика, Фурье, Ньютона).

4. От каких величин зависит коэффициент h вязкости газов?

5. В чём заключается метод определения `l и d?

6. Выведите расчётные формулы (7) и (12).

 

Поделиться:

Воспользуйтесь поиском по сайту: