 |
Определение удельной теплоемкости металлов методом охлаждения
|
|
|
|
| Составили: | Самсонова Н.П., Ярков Д.М. |
Тюмень, 2004г.
№ 5-м.ф.ОПРЕДЕЛЕНИЕ УДЕЛЬНОЙ ТЕПЛОЕМКОСТИ МЕТАЛЛОВ МЕТОДОМ ОХЛАЖДЕНИЯ.
| ЦЕЛЬ РАБОТЫ: | методом охлаждения измерить значение удельной теплоемкости стального образца. |
| ОБОРУДОВАНИЕ: | вольтметр, электропечь, термопара, металлические образцы. |
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ.
Удельной теплоемкостью с `вещества называют физическую величину, численно равную количеству теплоты, которое нужно сообщить единице массы, чтобы повысить его температуру на один градус.
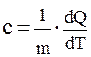
m- масса вещества, dT- изменение температуры тела в результате подвода к нему количества теплоты dQ.
Всякое тело, имеющее температуру выше окружающей среды, будет охлаждаться, причем скорость охлаждения зависит от величины теплоемкости тела. Эта зависимость лежит в основе метода определения теплоемкости металлов, рассматриваемого в данной работе. При охлаждении двух тел определенной формы можно снять кривые охлаждения- зависимость температуры от времени. Сравнение кривых охлаждения этих тел позволяет при известной теплоемкости одного найти теплоемкость другого. Рассмотрим это подробнее.
При охлаждении образца металла массой m количество отданной им теплоты dQ равно
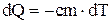(1)
c- удельная теплоемкость металла, dT- изменение его температуры.
С другой стороны, количество теплоты dQ, проходящее через поверхность соприкосновения площадью S за время dt, определяется формулой:
(2)
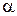- коэффициент теплоотдачи. Уравнение (2) представляет собой уравнение теплоотдачи, Т- температура рассматриваемого тела (в нашем случае температура образца), Т0- температура окружающей среды, с которой контактирует данное тело (здесь это комнатная температура). S в нашем случае- площадь поверхности образца.
|
|
|
Приравнивая правые части уравнений (1) и (2), получаем
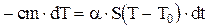
или
Проинтегрировав левую и правую части этого уравнения, запишем
(3)
А- постоянная интегрирования. Учитывая начальные условия опыта: при t=0, Т=Тmax, находим, что
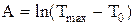
Тогда уравнение (3) перепишется
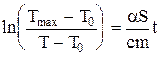
Выражая массу m образца через его объем V и плотность r металла, m= rV, окончательно получим
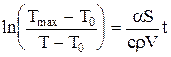(4)
Зависимость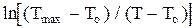 
от t представляет собой уравнение прямой линии. Величина 
есть тангенс угла наклона этой прямой к оси времени, т.е.
.
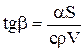Построив графики, соответствующие выражению (4), для двух образцов и определив по ним значения тангенсов углов наклона к оси времени, возьмем их отношение, обозначив его через h
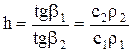(5)
Величины a, V и S принимаем одинаковыми для обоих образцов в одних и тех же интервалах температур.
Из уравнения (5) теплоемкость неизвестного образца
(6)
ОПИСАНИЕ УСТАНОВКИ.
Схема установки изображена на рис. 1. Внутри электропечи находится металлический образец, который представляет собой цилиндр с высверленным с одного конца каналом. Температура образца измеряется с помощью термопары, помещенной в канал образца. Концы термопары подведены к вольтметру цифровому универсальному В7-21.
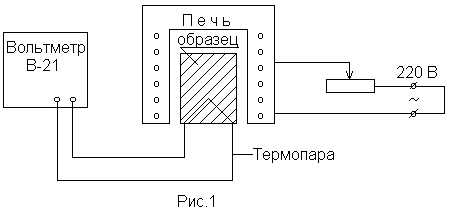
При включении в сеть печи и нагревании образца, в цепи, содержащей термопару, возникает термоэдс. Величина термоэдс пропорциональна разности температур e~(Т-То).
Таким образом, если вместо (Т-То) в уравнение (4) поставить e, а вместо (Тmax-То) - emax, то уравнение
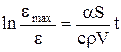, (7)
где emax - величина термоэдс, соответствующая максимальной температуре нагрева образца.
Значение термоэдс снимаются с цифрового вольтметра В7-21.
Построив графики зависимости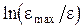 
для различных металлов, и определив для них тангенсы углов наклона к оси времени, можно определить неизвестную теплоемкость, если дана теплоемкость одного из металлов.
|
|
|
Примерный вид графика зависимости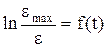 
приведен на рис.2.
|
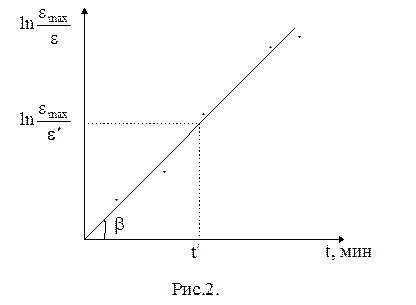
ИЗМЕРЕНИЯ И ИХ ОБРАБОТКА.
| 1. | Поместить первый образец с неизвестной теплоемкостью в электропечь. | ||||
| 2. | Отпустить электропечь и включить ее в сеть. | ||||
| 3. | Провода термопары вставить в клеммы «+» и «-» размещенные, на панели вольтметра. Включить вольтметр в сеть. | ||||
| 4. | Нагрев образца производить в течение 10-15 минут до 170оС, что соответствует термоэдс 6 мВ. | ||||
| 5. | Поднять печь (начинается охлаждение образца) и через каждую минуту записать значения термоэдс e по показаниям вольтметра. Отсчет времени вести по часам. emax = 6мВ в момент времени t = 0. Результаты занести в таблицу. | ||||
| t, мин | e, мВ | emax/e | ln(emax/e) | tg b1 | |
| 6. | Вынуть первый образец и поместить второй, с известной теплоемкостью. |
| 7. | Повторить п.п. 6-7 для второго образца |
| 8. | Построить графики зависимости 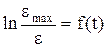для двух образцов и определить тангенсы углов наклона, tg b1 и tg b2.
|
| 9. | Определить неизвестную теплоемкость металла, считая, что теплоемкость второго известна и известны плотности металлов  , где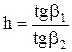  
|
| Примечание: | rмеди = 8.6×103 кг/м3 |
| rстали = 7.7×103 кг/м3 | |
| смеди = 395 Дж/кг×К |
КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Дать определение теплоемкости. От чего она зависит?
2. Чему равно количество теплоты, теряемое металлом?
3. Записать уравнение теплоотдачи.
4. В чем заключается принцип определения теплоемкости металлов?
5. Вывести формулу (6).
ЛИТЕРАТУРА.
1. Трофимова Т.И. Курс физики. М., 1985.
2. Савельев И.В. Курс общей физики. т.1. М., 1982.
|
|
|
