 |
Простые проявления поверхностного натяжения
|
|
|
|
Так как при фиксированном объёме наименьшей поверхностью обладает шар, то в условиях невесомости жидкость принимает форму шара. В условиях земного тяготения лишь сравнительно небольшие капли принимают форму шара. Небольшие ртутные шарики также служат хорошей иллюстрацией проявления поверхностного натяжения. Если взять две жидкости с почти одинаковыми плотностями, но такие, чтобы они не смешивались, то небольшое количество одной из них, введённое в другую жидкость, принимает форму шара. В этом случае архимедова сила уравновешивает силу тяжести, и поверхностное натяжение проявляется почти в чистом виде.
Условия равновесия на границе раздела двух жидкостей
Если на поверхность одной жидкости поместить каплю другой, более лёгкой, то возможны два результата в зависимости от соотношения поверхностных натяжений (рисунки 3а, 3б). Если обозначить dl элемент длины, направленный вдоль линии соприкосновения трёх сред 1,2,3, то силы поверхностного натяжения, действующие на этот элемент, равны 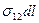 ,
,  ,
,  . Заметим, что элемент dl направлен перпендикулярно плоскости чертежа. Если
. Заметим, что элемент dl направлен перпендикулярно плоскости чертежа. Если  то равновесие реализуется в виде ситуации изображенной на рис.3 а. Условием равновесия является обращение в нуль равнодействующих на элемент dl:
то равновесие реализуется в виде ситуации изображенной на рис.3 а. Условием равновесия является обращение в нуль равнодействующих на элемент dl:
 ,
,

Система этих уравнений позволяет определить углы  и
и  , которые называются краевыми.
, которые называются краевыми.

Рисунок 3а,б - Условия равновесия на поверхности двух жидкостей
Если же  , то равновесная ситуация указанного вида невозможна и капля 2 растечется по всей поверхности жидкости 1 в виде тонкого молекулярного слоя (рисунок 3, б).
, то равновесная ситуация указанного вида невозможна и капля 2 растечется по всей поверхности жидкости 1 в виде тонкого молекулярного слоя (рисунок 3, б).
Условия равновесия на границе жидкость - твердое тело
В этом случае возможны равновесные ситуации, показанные на рисунке 4 а,б, в. 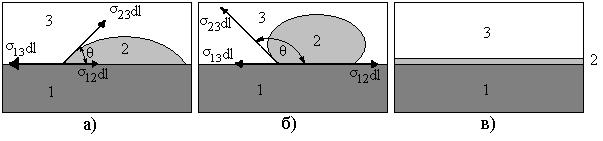
|
|
|
Рисунок 4 -Условия равновесия на границе жидкости с твердым телом
Условие равновесия при этом имеет соответственно вид
 . Если
. Если  , жидкость растекается по поверхности тела молекулярным слоем. Говорят, что она смачивает поверхность твёрдого тела. Это случай полного смачивания.
, жидкость растекается по поверхности тела молекулярным слоем. Говорят, что она смачивает поверхность твёрдого тела. Это случай полного смачивания.
Поверхностно-активные вещества
Поверхностная энергия стремиться достигнуть минимального значения. Это возможно вследствие уменьшения, как площади поверхности, так и поверхностного натяжения σ. Поэтому при добавлении в жидкость другой жидкости с меньшим поверхностным натяжением последняя будет адсорбироваться в поверхностном слое, в результате чего поверхностное натяжение уменьшиться. Такое вещество называется поверхностно-активным (например, мыло). Другие вещества увеличивают поверхностное натяжение (например, раствор сахара, растворы различных солей и т.д.). Такое вещество, наоборот, концентрируется вне поверхностного слоя жидкости. При его добавлении в раствор, содержащий поверхностно - активные вещества, последние интенсивно выталкиваются на поверхность. Например, добавление соли в мыльный раствор вызывает вытеснение мыла на поверхность раствора.
МЕТОДИКА ЭКСПЕРИМЕНТА
Представим, что жидкость медленно накапливается на конце вертикально поставленной трубки и при достижении некоторого количества отрывается в виде капли. Непосредственно перед отрывом капля висит на шейке, форму которой можно приблизительно считать цилиндрической. Сила тяжести капли Fт уравновешивается силами поверхностного натяжения, действующими по контуру, ограничивающему поперечное сечение шейки. Результирующую этих сил можно представить в виде:
Fн=πdσ, (3)
где d – диаметр шейки, м;
σ – коэффициент поверхностного натяжения, Н/м;
π=3,14.
Очевидно, что в момент отрыва сила поверхностного натяжения на шейке капли, направленная вертикально вверх, как раз равна силе тяжести действующей на каплю (рисунок 5) Fт = Fн. Если диаметр шейки капли d, то Fт = πdσ. Отсюда
|
|
|
 σ = Fт/πd (4)
σ = Fт/πd (4)
Таким образом, определение коэффициента поверхностного натяжения сводится к определению силы тяжести, действующей на каплю и диаметра шейки в момент ее отрыва. Сила тяжести, действующая на каплю, определяется по объему V и плотности жидкости ρ
Fт= m·g=ρgV/n (5)
 Где ρ – плотность жидкости, кг/м3;
Где ρ – плотность жидкости, кг/м3;
g=9,8 м/с2 ускорение свободного падения;
V – объём жидкости,м3;
n– число капель в данном объеме;
Подставим (5) в (4), получим расчетную формулу
σ = ρgV/nπd (6)
Схема экспериментальной установки приведена на рисунке 6.

Рисунок 6 - Схема экспериментальной установки
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1) Наполнить шприц исследуемой жидкостью.
2) Накапать в чашечку 1мл жидкости, подсчитав при этом количество капель.
3) Измерение провести 3 раза.
4) Полученные данные занести в таблицу 1.
5) Повторить пункты 1-4 для воды комнатной температуры, горячей воды, воды со льдом, водного раствора поваренной соли (NaCl) и мыльной воды.
6) Измерить температуру воды с помощью термометра. Плотность воды при данной температуре определить по таблице 2, занести в таблицу 1. Значение плотности водного раствора соли - получить у лаборанта. Плотность мыльного раствора принять равным плотности воды при данной температуре.
7) Рассчитать σ по формуле (6), учитывая, что диаметр капилляра d=(2,3 + 0,1) мм
8) Оценить полученные результаты, сделать вывод (ответить на вопрос- как влияют на коэффициент поверхностного натяжения повышение температуры, добавление в воду соли или мыла).
Таблица 1 - Результаты измерений
| Вода при комнатной температуре | |||||
| № | V, м3 | ρ, кг/м3 | n |  , Н/м , Н/м
| t,°C |
| ср.зн. | |||||
| Горячая вода | |||||
| № п/п | V, м3 | ρ, кг/м3 | n |  , Н/м , Н/м
| t,°C |
| ср.зн. | |||||
| Холодная вода | |||||
| № п/п | V, м3 | ρ, кг/м | n |  , Н/м , Н/м
| t,°C |
| ср.зн. | |||||
| Водный раствор соли | |||||
| № п/п | V, м3 | ρ, кг/м3 | n |  , Н/м , Н/м
| t,°C |
| ср.зн. | |||||
| Мыльная вода | |||||
| № п/п | V, м3 | ρ, кг/м3 | n |  , Н/м , Н/м
| t,°C |
| ср.зн. |
|
|
|
Таблица 2 - Зависимость плотности дистиллированной воды от температуры
t, 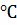
| ρ, кг/  3 3
| t, 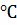
| ρ,кг/  3 3
|
| 999,841 | 998,406 | ||
| 999,900 | 998,205 | ||
| 999,941 | 997,994 | ||
| 999,965 | 997,772 | ||
| 999,973 | 997,540 | ||
| 999,965 | 997,299 | ||
| 999,941 | 997,047 | ||
| 999,902 | 996,785 | ||
| 999,849 | 996,515 | ||
| 999,782 | 996,235 | ||
| 999,701 | 995,946 | ||
| 999,606 | 995,649 | ||
| 999,498 | 992,220 | ||
| 999,377 | 988,040 | ||
| 999,244 | 983,200 | ||
| 999,099 | 977,760 | ||
| 998,43 | 971,790 | ||
| 998,775 | 965,300 | ||
| 998,596 | 958,350 |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Как возникают силы поверхностного натяжения?
2 Физический смысл коэффициента поверхностного натяжения.
3. Единицы измерения коэффициента поверхностного натяжения.
5.От чего зависит коэффициент поверхностного натяжения?
4. Приведите примеры проявления силы поверхностного натяжения.
5. Объясните явления смачивания.
6. Что такое поверхностно-активные вещества?
7. Выведите расчётную формулу (6).
8.Решите задачу: считая процесс образования мыльного пузыря изотермическим, определить работу А, которую надо совершить, чтобы увеличить его диаметр от d1=2 см до d2=6см. Поверхностное натяжение σ мыльного раствора принять равным 40 мН/м.
Библиографический список
Основная литература:
1.Трофимова, Т.И. Курс физики. - М: Академия, 2007.- 560 с.
Дополнительная литература:
2.Матвеев, А.Н. Молекулярная физика. М.:Высшая школа,1987. 360с.
3.Детлаф, А.А., Яворский Б.М. Курс физики. М.: Высшая школа, 2001. 718 с.
4.Кухлинг, Х. Справочник по физике.- М., 1982.- 520с.
|
|
|


