Методические указания к лабораторной работе № 8-м. Ф.

Кафедра физики

«Определение теплопроводности воздуха методом нагретой нити»

Составили:	Самсонова Н.П. Ничипорук Л.С.

Тюмень 2005г.

 

№ 8-м.ф.ОПРЕДЕЛЕНИЕ ТЕПЛОПРОВОДНОСТИ ВОЗДУХА

Цель работы: определить коэффициент теплопроводности воздуха.

Оборудование: модуль “теплопроводность газов” 06, измерительная система “ИСТ-3”, провод Ш4-Ш4 черный и красный к мультиметру, кабель аудио моно “тюльпан”, два провода Ш4-Ш4.

 

КРАТКАЯ ТЕОРИЯ

В термодинамически неравновесных системах возникают особые необратимые процессы, называемые явлениями переноса, в результате которых происходит пространственный перенос энергии, массы, импульса. К явлениям переноса относятся теплопроводность (обусловлена переносом энергии), диффузия (обусловлена переносом массы), и внутреннее трение (обусловлено переносом импульса.

Исходя из представлений молекулярно-кинетической теории, выведем общее для явлений переноса уравнение переноса. Выделим в стенке сосуда некоторую элементарную площадку D S (рис.1). Ориентируем ось 0 х перпендикулярно площадке D S. Необходимо учитывать, что реально молекулы движутся к площадке D S под разными углами и имеют различные скорости, причем скорость молекул при каждом соударении меняется. Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных направлений, так что в любой момент времени вдоль каждого из них движется 1/3 молекул, причем половина молекул1/6 движется вдоль данного направления в одну сторону, половина в противоположную. Тогда число молекул N, движущихся в одном направлении, через площадку D S за время D t равно

, (1)

где n₀- концентрация молекул, ν- средняя скорость движения молекул.

 

 

Рис.1

 

Эти молекулы переносят через площадку D S значения своих физических характеристик (массу, энергию, импульс). Обозначим физическую характеристику, переносимую молекулами, буквой j. Тогда количество физической характеристики, перенесенное молекулами в одном направлении через площадку D S за время D t, равно

(2)

Очевидно, что такое же количество будет перенесено и обратно.

Предположим, что газ неоднороден по своим свойствам, т.е. концентрация n₀ его молекул различна в разных местах объема и сами молекулы имеют неодинаковые значения физической величины j. Пусть количество n₀j убывает в положительном направлении О х, будучи равным (n₀j)₁ слева от площадки D S и (n₀j)₂ - справа от нее. В этом случае имеет место преимущественный перенос физической величины Nj через площадку D S слева направо.

 

Рис. 2

 

Он равен

(3)

Обмен значениями j и изменение концентрации n₀происходит только при взаимостолкновениях молекул, т.е. на расстоянии l, равном средней длине свободного пробега молекул. Поэтому можно положить, что значения n₀j сохраняются неизменным на расстоянии l влево и вправо от DS. На этих расстояниях и будем брать значение n₀j (рис.2). Умножим и разделим на 2 l правую часть последнего равенства:

(4)

Отношение

представляет собой градиент n₀j. Тогда формула (4) примет вид:

(5).

Знак минус обусловлен тем, что перенос физической величины происходит в направлении, противоположном градиенту. Формула (5) называется уравнением переноса. На его основе рассмотрим конкретное явление переноса- теплопроводность.

Пустьв некотором объеме газа температура Т убывает в направлении О х

Рис.3

 

Это возможно, когда в левой части объема О имеется нагреватель. Обозначим через Т₁ и Т₂ температуры на расстояниях l от площадки D S. Причем Т₁ > Т₂. Кинетическая энергия молекулы газа равна

, (6)

где k -постоянная Больцмана, i - число степеней свободы. Тогда энергия молекул W₁, находящихся слева от DS, больше, чем энергия молекул W₂, находящихся справа от D S. Поэтому в направлении убывания температуры будет происходить перенос энергии, а следовательно, и количество теплоты Q. Применяя уравнение переноса (5), заметим, что переносимой физической характеристикой является энергия молекулы, т.е. j = W. Тогда, поскольку концентрацию молекул n₀ можно считать постоянной во всем объеме газа, запишем:

. (7)

Учитывая выражение (5), получим

. (8)

Очевидно, что , (9)

где Q - количество теплоты, переносимое за время D t через площадку D S, перпендикулярную направлению убывания температуры.

Подставляя уравнения (8) и (9) в уравнение (7) получим:

(10)

Т.к , где N - число молекул в объеме V,

, где R - универсальная газовая постоянная, N_A - число Авогадро, то

, (11)

где (12)- количество вещества, m -масса газа, -молярная масса газа.

Учитывая (11) и (12), получим

, (13)

где - плотность газа, удельная изохорная теплоемкость определяется:

. (14)

Подставляя (11)-(14) в уравнение (10), получим

. (15)

Обозначим - коэффициент теплопроводности газов, тогда

. (16)

Уравнение (16) называется уравнением теплопроводности, или уравнением Фурье.

Т.к l~ , а r ~ р, то lr не зависит от давления, т.е теплопроводность не зависит от давления. Однако у сильно разреженных газов (когда длина свободного пробега превышает размер сосуда) теплопроводность пропорциональна давлению. Величина c возрастает с температурой чуть больше чем .

 

 

ОПИСАНИЕ УСТАНОВКИ.

 

Рис.5. Схема соединений

Рис.4. Модуль 06 “Теплопроводность газов”

Модуль 06 “Теплопроводность газов” (рис.4) предназначен для измерения теплопроводности воздуха и других газов методом нагретой нити. Узел размещен на панели 4. Металлическая нить 5 (сплав на основе никеля) натянута между стойками 1 по оси цилиндрического канала в корпусе 2. Канал закрыт пробками 3. В корпус ввернут датчик температуры Д.

Схема соединений показана на рис.5. Нить 1 подключена к гнездам “U_Н” на панели модуля. Последовательно с нитью включен эталонный резистор R_{ЭТ ,} подключенный к гнездам “U_ЭТ”. Источник питания подключают к гнездам “ПИТ”. Измерив напряжение на нити “U_Н” и на резисторе “U_ЭТ”_, определяют сопротивление нити и выделяющуюся в ней тепловую мощность. Схема построена так, что по сопротивлению нити определяют ее температуру. Оценивая тепловую мощность нити, находят теплопроводность газа.

 

МЕТОД ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ТЕПЛОПРОВОДНОСТИ ВОЗДУХА.

 

Уравнение Фурье можно представить в виде:

, (17)

где dq -количество теплоты, переносимое в единицу времени через площадку 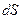при температурном градиенте .

Для измерения коэффициента теплопроводности газов используют прибор, состоящий из двух длинных коаксиальных цилиндров, пространство между которыми заполняется исследуемым газом. В нашем случае это цилиндрическая нить а диаметром d, натянутая по оси цилиндрического канала корпуса b диаметром D, заполненого воздухом (рис.6).

	Рис.6. Схема коаксиальных цилиндров

 

Из уравнения (1) найдем полный поток тепла, проходящий между цилиндрами. Для этого выделим в газе цилиндрическую поверхность радиуса х. В силу симметрии системы величина одинакова для всех точек, лежащих на нашей поверхности. Тогда проинтегрируем (17) по всей поверхности:

, (18)

где -площадь боковой поверхности цилиндра.

В установившемся режиме q - поток тепла через цилиндрическую поверхность радиуса х не зависит от χ. Поэтому выражение (18) проинтегрируем, считая q =const:

,

где t -температура нагретой нити, t_K - температура корпуса. Тогда

,

откуда

. (19)

По закону сохранения и превращения энергии

, (20)

где P -тепловая мощность, выделяемая в нити сопротивлением R при прохождении тока I.

Т.к. нить и эталонный резистор R_ЭТ соеденены последовательно, то сила тока в нити

, (21)

где U_ЭТ - напряжение на эталонном резисторе, а сопротивление нити равно

, (22)

где U_Н - напряжение на нити.

Зависимость сопротивления нити R от температуры t имеет вид:

, (23)

где R₀ - сопротивление при 0⁰С, α - температурный коэффициент сопротивления.

Измерив сопротивление нити R₁ при начальной температуре t₁ (при малых токах) и сопротивление R при искомой температуре t, подставим их в уравнение (23), получим:

(24),(25)

Решая совместно уравнения (24) и (25), найдем температуру нити t:

. (26)

 

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Подключить модуль 06 (гнезда “ПИТ”) к источнику питания ИСТ-3 (гнезда “НАГР” “ОБЩ”) двумя синими проводами Ш4-Ш4.

2. Кабелем “аудио моно “тюльпан” соединить вход “Д1” ИСТ-3 с датчиком температуры корпуса модуля 06 (белый проводок в верхнее гнездо “ДАТ”, черный- в нижнее).

3. Включить ИСТ-3 (тумблеры “СЕТЬ”, “~”,“ВКЛ” переключить в верхние положения).

4. Нажать кнопку “Т₁” ИСТ-3.

5. Ручки “АМПЛИТУДА” и “ТЕМПЕРАТУРА”- не трогать!

6. Ручку “НАГРЕВ” поставить на 0 вращением против часовой стрелки до упора.

7. Подключить проводами Ш4-Ш4 мультиметр (“красный”- разъему “VΩmА”, “черный”- к заземлению “СОМ”) к гнездам “U_ЭТ” модуля 06.

8. Переключателем мультиметра выбрать предел измерения 200 мВ

9. Для измерения сопротивления нити R₁ при начальной температуре t₁ с помощью ручки “НАГРЕВ” подать на эталонный резистор напряжение 160-170 мВ. Записать в табл.1 U_ЭТ (в В), а также показания t₁ (в ⁰С) с цифрового индикатора ИСТ-3.

10. Переключив провода мультиметра в гнезда “U_Н”, записать показания напряжения на нити U_Н (в В) в табл.1.

11. Мультиметр после каждого измерения отключать в положение “OFF”.

12. Для определения коэффициента теплопроводности χ подать на эталонный резистор напряжение от 2 до 4В. Предел измерения мультиметра выбрать 20В.

13. Мультиметром поочередно измерить напряжения U_ЭТ и U_Н (аналогично п.п 9-10). Занести показания U_ЭТ, U_Н и t_К (с цифрового индикатора) в таблицу 2. Измерение провести для 3-5 значений U_ЭТ.

14. Рассчитать силу тока в нити I по формуле (21) для начальной (табл.1) и для искомых температур (табл.2).

15. Вычислить по формуле (22) сопротивление нити: R₁ в табл.1 при начальной температуре t₁; R в табл.2 при искомых температурах.

16. По формулам (20) и (26) определить мощность нити Р и температуру нагретой нити t (искомую температуру) для всех значений U_ЭТ. Результаты занести в табл.2.

17. По формуле (19), принимая q = Р, рассчитать коэффициенты теплопроводности для всех значений U_ЭТ. Результаты занести в таблицу 2.

ДАННЫЕ УСТАНОВКИ:

диаметр нити d =0,10 мм;

диаметр канала корпуса D =12 мм;

длина нити L =0,24 м;

температурный коэффициент сопротивления α =5,6·10^-31/град.

сопротивление эталонного резистора R_ЭТ =10 Ом.

 

ТАБЛИЦА 1. Результаты измерений при начальной температуре.

UЭТ , В	UН, В	I, А	R1, Ом	t1, 0С

 

ТАБЛИЦА 2. Результаты измерений при искомой температуре.

№ п.п	UЭТ , В	UН, В	I, А	R, Ом	Р, Вт	tК, 0С	t, 0С	χ, Вт/(мК)

 

КОНТРОЛЬНЫЕ ВОПРОСЫ.

1. Дать характеристику явлениям переноса

2. Вывести общее уравнение переноса (5).

3. Получить уравнение теплопроводности (уравнение Фурье).

4. Физический смысл коэффициента теплопроводности, единица измерения.

5. От чего зависит коэффициент теплопроводности газов?

6. В чем заключается метод определения коэффициента теплопроводности в данной работе? Вывести расчетную формулу (19).

7. Как определяется температура нагретой нити?

 

ЛИТЕРАТУРА

1. Трофимова Т.И. Курс физики. М., 2004г.

2. Детлаф А.А, Яворский Б.М. Курс физики. М., 2004г.

3. Кухлинг Х. Справочник по физике. М., 1982 г.

 

 

x

Поделиться:

Воспользуйтесь поиском по сайту: