Определение скорости звука в газе методом стоячих волн в трубе.

Федеральное агентство по образованию ГОУ ВПО

 

 

ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ   АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ   УНИВЕРСИТЕТ

Кафедра физики

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ЛАБОРАТОРНОЙ РАБОТЕ № 9-м.ф

«Определение показателя адиабаты воздуха методом интерференции звуковых волн»

Составили:

Самсонова Н.П. Тимерзянова И.И.

Тюмень 2007г.

№ 9-м.ф Определение показателя адиабаты воздуха методом интерференции звуковых волн.

 

 

Цель работы: Определить отношение C_p/C_v в диапазоне температур методом интерференции звуковых волн.

Оборудование: Модуль «Резонатор», измерительная система «ИСТ-3».

 

КРАТКАЯ ТЕОРИЯ.

Введение

 

Упругими волнами называют механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольные и поперечные. В продольных волнах частицы среда колеблются в направлении распространении волны, в поперечных волнах – в плоскостях перпендикулярных направлению распространения волны.

Звуковыми (или акустическими) волнами называются распространяющиеся в среде упругие волны, обладающие частотами в пределах 16—20000 Гц.

По частоте колебаний звуковые волны классифицируют сле­дующим образом: инфразвук (0—16 Гц), слышимый звук (16 Гц —20 кГц), ультразвук (20 кГц—103 МГц), гиперзвук (свыше 103 МГц).

Звуковые волны в газах и жидкостях могут быть только продольными, так как эта среды обладают упругостью лишь по отношению к деформациям сжатия (растяжения). В твердых телах звуковые волны могут быть как продольными, так и поперечными, так как твердые тела обладают упругостью по отношению к деформациям сжатия (рас­тяжения) и сдвига.

Звуки подразделяют на музыкальные тона и шумы. Музыкальным тоном называют звук какой-либо определенной частоты, который создается гармо­нически колеблющимся телом. Шум представляет собой сложный звук, образующийся в результате длительных непериодических колебаний различных источников звука (шум моря, деревьев, толпы и т. д.)

Характеристики звука

 

Звуки, которые мы слышим, вызывают у нас различные ощу­щения. Это различие имеет субъективный характер, т. е. один и тот же звук может по-разному оцениваться различными людь­ми. Существуют три такие субъективные оценки звука — гром­кость, высота тона и тембр. Выясним, какие объективные харак­теристики звука соответствуют этим оценкам. Для этого необхо­димо с помощью микрофона преобразовать звук в электрический ток и исследовать его с помощью осциллографа.

Осциллограммы (рис. 1) показывают, что гром­кость звука зависит от амплитуды колебаний и, следовательно, от интенсивности звука.

 

Интенсивностью звука (или силой звука) называется величина, определяемая сред­ней по времени энергией, переносимой звуковой волной в единицу времени сквозь единичную площадку, перпендикулярную направлению распространения волны:

Единица интенсивности звука в СИ — ватт на метр в квадрате (Вт/м²).

Чувствительность человеческого уха различна для разных частот. Для того чтобы вызвать звуковое ощущение, волна должна обладать некоторой минимальной интенсив­ностью, но если эта интенсивность превышает определенный предел, то звук не слышен и вызывает только болевое ощущение. Таким образом, для каждой частоты колебаний существуют наименьшая (порог слышимости) и наибольшая (порог болевого ощущения) интенсивности звука, которые способны вызвать звуковое восприятие. На рис. 2 представлены зависимости порогов слышимости и болевого ощущения от частоты звука. Область, расположенная между этими двумя кривыми, является областью слышимости.

Если интенсивность звука является величиной, объективно характеризующей вол­новой процесс, то субъективной характеристикой звука, связанной с его интенсив­ностью, является громкость звука, зависящая от частоты. Согласно физиологическому закону Вебера — Фехнера, с ростом интенсивности звука громкость возрастает по логарифмическому закону. На этом основании вводят объективную оценку громкости звука по измеренному значению его интенсивности:

где Iо — интенсивность звука на пороге слышимости, принимаемая для всех звуков равной 10^-12 Вт/м². Величина L называется уровнем интенсивности звука и выражается в белах (в честь изобретателя телефона Белла). Обычно пользуются единицами, в 10 раз меньшими, — децибелами (дБ).

Физиологической характеристикой звука является уровень громкости, который вы­ражается в фонах (фон). Громкость для звука в 1000 Гц (частота стандартного чистого тона) равна 1 фон, если его уровень интенсивности равен 1 дБ. Например, шум в вагоне метро при большой скорости соответствует ≈90 фон, а шепот на расстоянии 1 м — ≈ 20 фон.

Реальный звук является наложением гармонических колебаний с большим набором частот, т. е. звук обладает акустическим спектром, который может быть сплошным (в некотором интервале присутствуют колебания всех частот) и линейчатым (присутству­ют колебания отделенных друг от друга определенных частот).

Высота зву­ка — качество звука, определяемое человеком субъективно на слух и зависящее от частоты звука. С ростом частоты высота звука увеличивается, т. е. звук становится «выше». Характер акустического спектра и распределения энергии между определен­ными частотами определяет своеобразие звукового ощущения, называемое тембром звука. Так, различные певцы, берущие одну и ту же ноту, имеют различный акустичес­кий спектр, т. е. их голоса имеют различный тембр.

 

Волновые процессы в газе

 

При нормальных условиях расстояние между молекулами газа (порядка 10^-7м) гораздо меньше длины звуковой волны (0,2<λ<20м). Поэтому молекулярное строение газа (прерывистость – вещества) можно не учитывать и считать среду (газ) сплошной.

Рассмотрим плоскую волну, распространяющуюся в направлении оси x со скоростью υ, которая описывается уравнением:

x(x,t)=Acos(wt-kx) (1)

где ξ – смещения тонкого слоя газа, зависит от координаты x слоя в невозмущенном состоянии и от времени t;

- волновое число;

l=uT- длина волны;

- циклическая чистота;

А = ξ_m максимальное смешение слоя от положения равновесия.

Дифференцируя уравнения волны (1) по времени, получим:

1.Уравнение волны для скорости колебательного движения – колебательной скорости:

(2)

=А ω амплитуда колебательной скорости.

2. Уравнение волны для ускорения колебательного движения – колебательного ускорения:

a_k = (3)

Где а_кm =А ω² - амплитуда колебательного ускорения,

Выделим в области волны цилиндрический объем высотой c площадью основания S_n. Пусть основание цилиндра с координатой имеет в некоторый момент времени следующие 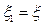, то смещение основания с координатой будет (рис. 3)

Рис. 3 Смещение слоев газа в выделенном объеме.

Следовательно, рассматриваемый объем деформируется – он получает удлинение ( - алгебраическая величина; - соответствует сжатию цилиндра).

Объем газа между слоями , тогда изменение объема (удлинение) . Найдем относительное изменение объема газа:

(4)

дифференцируя (4) второй раз по x, получим:

Учитывая (3), получим:

(5)

Уравнение (5) является волновым уравнением, решением которого является уравнение (1).

Упругая волна в газе представляет собой распространяющуюся в пространстве последовательность чередующихся областей сжатия и разряжения газа. Как показывает опыт, сжатие в любом слое настолько быстро во времени сменяется разрежением, что температуры соседних областей сжатия и разрежения, не успевают выравниваться. Т.е. распространение звука представляет собой адиабатный процесс. Найдем изменение давления, обусловленное сжатием и разряжением. Для этого продифференцируем уравнение Пуассона для адиабатного процесса: , где - показатель адиабаты, равный отношению теплоемкости газа при постоянном давлении С_Р к теплоемкости при постоянном объеме С_V.

_, откуда

(6)

Учтя (4), находим:

(7)

На газ, заключенный между слоями (рис. 3), слева и справа действуют противоположно направленные силы, обусловленные акустическим давлением в этих слоях:

(8)

(9)

Согласно второму закону Ньютона, равнодействующих сил F₁ и F₂ сообщает колебательное ускорение α_k массы газа в объеме :

(10)

Откуда

или (11)

Уравнение (11) является волновым сравнивая его с уравнением (5) получим

(12)

Из уравнения Менделеева – Клапейрона найдем:

(13)

Поставив уравнение (13) в уравнение (12), определим отношение теплоемкостей:

(14)

Таким образом, для определения показателя адиабаты достаточно измерить температуру газа и скорость распространения звука.

Определение скорости звука в газе методом стоячих волн в трубе.

При сложении когерентных волн возникает интерференция, заключающаяся в том, что колебания в одних точках усиливают, а в других точках ослабляют друг друга.

Волны, образующиеся при наложении двух встречных плоских волн с одинаковыми амплитудами и частотами, называются стоячими. Практически стоячие волны возникают при отражении волн от преград. Падающая на преграду и бегущая ей на встречу отраженная, налагаясь друг на друга, дают стоячую волну.

Напишем уравнения двух таких плоских волн:

ξ₁=Acos(ωt-kx)

ξ₂=Acos(ωt+kx). (14)

Сложим эти уравнения и учитывая, что , получим уравнение стоячей волны:

(15)

Из него видно, что колебания стоячей волны той же частоты, что и у встречных волн, причем амплитуда А_ст оказывается зависящей от х:

А_ст=2Асоs .

В точках, где:

(n=0,1,2,……), (16)

амплитуда колебаний достигает максимального значения 2А. Эти точки называются пучностями стоячей волны. Из условия (16) найдем координаты пучностей:

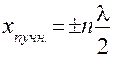. (17)

В точках, где

(n=0,1,2,……),

амплитуда колебаний обращается в нуль. Эти точки называются узлами стоячей волны. Точки среды, находящиеся в узлах, колебаний не совершают. Координаты узлов имеют следующие значения:

(n=0,1,2,…..) (18)

Из формулы (17) и (18) следует, что расстояния между двумя соседними пучностями и узлами одинаковы и равны . Пучности и узлы сдвинуты относительно друг друга на .

Стоячие волны возникают при отражении как от менее плотной, так и от более плотной среды. Если среда, от которой происходит отражение, менее плотная, то в месте отражения возникает пучность (рис.4,б). Образование узла связано с тем, что волна, отражаясь от более плотной среды меняет фазу на противоположную и у границы происходит сложение колебаний с противоположными фазами, в результате чего получается узел. Если же волна отражается от менее плотной среды, изменение фазы не происходит и у границы колебания складывается с одинаковыми фазами – образуется пучность.

В бегущей волне происходит перенос энергии колебательной движения в направлении ее распространения. В стоячей волне переноса энергии нет, т.к падающие и отраженные волны одинаковой амплитуды несут одинаковую энергию в противоположный направлени

Рис.4. Образование стоячей волны при отражении

а)от менее плотной среды;

б)от более плотной среды.

В среде, имеющей ограниченный размер l, стоячая волна может образоваться только в том случае, когда длина l кратна целому числу :

l=n . (19)

где λ – длина бегущей волны,

n – 1,2,3,…. – целое число.

Звуковые колебания, распространяющиеся вдоль трубы, испытывают многократные отражения от торцов. Если условие (19) выполнено, то волна, отраженная от заднего торца трубы, вернувшаяся к ее началу и вновь отраженная, совпадает по фазе с падающей. Совпадающие по фазе волна усиливают друг друга. Амплитуда звуковых колебаний при этом резко возрастает - наступает резонанс.

Скорость звука υ связана с частотой ν и длиной волны λ соотношением:

υ= λ ν (20)

Плавно изменяя частоту звукового генератора, а следовательно, длину звуковой волны (при постоянной длине трубы), получим для последовательных резонансов:

(21)

Из (20) и (21) найдем

υ=2l (ν₂- ν₁)

(22)

Описание установки

Для измерения скорости звука служит модуль «Резонатор», изображенный на рис.5.

Модуль содержит металлическую трубу 1 и пульт 6. один конец трубы закрыт крышкой, а другой – динамиком 4 и микрофоном5. На трубу намотана нагревательная обмотка 2. В трубу ввернут датчик температуры 3. Динамик подключен к генератору гармонического сигнала, микрофон – к индикатору резонанса (оба устройства входят в состав пульта).

Пульт «Резонатора» содержит генератор с регулируемой амплитудой и частотой (700-3000Гц), цифровой частотомер с4 – разрядным индикатором Н1, индикатор резонанса (светодиод) Н2, ручки регулировки частоты и амплитуды, органы коммутации. Электропитание всех устройств производится через разъем 7, подключаемый через кабель к разъему «Термостат» ИСТ-3.

Изменяя частоту сигнала, по максимумам амплитуды находят резонансные частоты ν₁ и ν₂ при различных температурах.

 

Рис.5. Модуль «Резонатор»

 

Поделиться:

Воспользуйтесь поиском по сайту: